Braille is een speciaal voor blinden ontwikkeld lees- en schrijfalfabet. Het werd ontwikkeld en geperfectioneerd door de Fransman Louis Braille (1809–1852) — die zelf op driejarige leeftijd blind was geworden — tot het in 1829 als bruikbare methode kon ingezet worden op het Parijse blindeninstituut waar hij verbleef. In 1854 werd het officieel als alfabet geaccepteerd.

Braille is een reliëfalfabet waarbij letters en andere aanduidingen door middel van puntjes in het papier gedrukt worden. Daardoor ontstaan kleine verhogingen die met de vingertoppen kunnen 'gelezen' worden. De zes puntjes die samen een brailleteken vormen, worden gerangschikt in een rooster van 2 bij 3 puntjes. Ze worden van linksboven naar linksonder genummerd als 1, 2 en 3, en van rechtsboven naar rechtsonder als 4, 5 en 6.
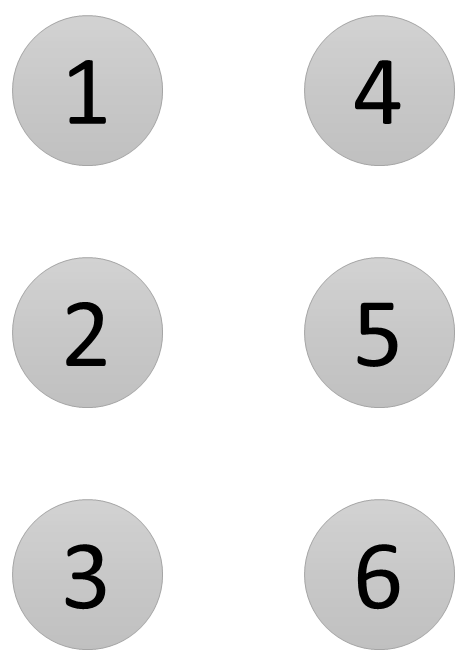
Omdat elk brailleteken altijd minstens één verhoogd puntje moet hebben, zijn er in totaal dus 63 mogelijke brailletekens.
| ⠀ | ⠁ (1) |
⠂ (2) |
⠃ (12) |
⠄ (3) |
⠅ (13) |
⠆ (23) |
⠇ (123) |
⠈ (4) |
⠉ (14) |
⠊ (24) |
⠋ (124) |
⠌ (34) |
⠍ (134) |
⠎ (234) |
⠏ (1234) |
| ⠐ (5) |
⠑ (15) |
⠒ (25) |
⠓ (125) |
⠔ (35) |
⠕ (135) |
⠖ (235) |
⠗ (1235) |
⠘ (45) |
⠙ (145) |
⠚ (245) |
⠛ (1245) |
⠜ (345) |
⠝ (1345) |
⠞ (2345) |
⠟ (12345) |
| ⠠ (6) |
⠡ (16) |
⠢ (26) |
⠣ (126) |
⠤ (36) |
⠥ (136) |
⠦ (236) |
⠧ (1236) |
⠨ (46) |
⠩ (146) |
⠪ (246) |
⠫ (1246) |
⠬ (346) |
⠭ (1346) |
⠮ (2346) |
⠯ (12346) |
| ⠰ (56) |
⠱ (156) |
⠲ (256) |
⠳ (1256) |
⠴ (356) |
⠵ (1356) |
⠶ (2356) |
⠷ (12356) |
⠸ (456) |
⠹ (1456) |
⠺ (2456) |
⠻ (12456) |
⠼ (3456) |
⠽ (13456) |
⠾ (23456) |
⠿ (123456) |
Opgave
Elke regel van het tekstbestand braille.txt bestaat uit een patroon $$p \in \mathcal{P}$$, gevolgd door een spatie en een woord $$w \in \mathcal{W}$$. De verzameling $$\mathcal{P}$$ bevat alle mogelijke omschrijvingen in Braille. Een omschrijving in Braille bestaat uit een opeenvolging van brailletekens, die telkens van elkaar gescheiden worden door één enkele spatie. Een brailleteken wordt voorgesteld als een reeks van minstens één cijfer, waarbij elk van de cijfers 123456 hoogstens één keer voorkomt en de cijfers in stijgende volgorde staan. De verzameling $$\mathcal{W}$$ bevat alle woorden die enkel bestaan uit kleine letters. Gevraagd wordt:
-
Bepaal zo kort mogelijke reguliere expressies voor de volgende deelverzamelingen van $$\mathcal{P}$$:
-
$$\mathcal{P}_1 = \{\,p \in \mathcal{P}\,|\,p\ $$heeft een even aantal brailletekens$$\,\}$$
voorbeeld: 1246 123456 123456 45 23456 356 1235 2356 $$\in \mathcal{P}_1$$15 46 25 1346 5 6 2 1456 2 145 23 $$\not \in \mathcal{P}_1$$ -
$$\mathcal{P}_2 = \{\,p \in \mathcal{P}\,|\,$$opeenvolgende brailletekens van $$p$$ hebben geen gemeenschappelijke puntjes$$\,\}$$
voorbeeld: 12456 3 4 12356 4 12356 4 12356 4 156 234 $$\in \mathcal{P}_2$$234 5 12456 13456 136 23456 2346 5 6 345 $$\not \in \mathcal{P}_2$$ -
$$\mathcal{P}_3 = \{\,p \in \mathcal{P}\,|\,p\ $$heeft minstens acht brailletekens met een puntje in de linkerbovenhoek of de rechteronderhoek$$\,\}$$
voorbeeld: 123456 126 2 12456 1256 4 46 12346 123456 4 56 $$\in \mathcal{P}_3$$24 245 1234 356 12346 6 3 346 245 5 12346 12356 $$\not \in \mathcal{P}_3$$ -
$$\mathcal{P}_4 = \{\,p \in \mathcal{P}\,|\,$$het eerste en het laatste brailleteken van $$p$$ hebben ofwel enkel puntjes aan de linkerkant ofwel enkel aan de rechterkant$$\,\}$$
voorbeeld: 456 1345 234 2 3456 2345 2356 12456 12 $$\in \mathcal{P}_4$$35 345 23 6 456 23456 123456 5 123456 5 256 $$\not \in \mathcal{P}_4$$
Geef telkens een Unix commando waarin de reguliere expressie gebruikt wordt door een commando uit de grep familie om enkel de regels van het tekstbestand naar stdout te schrijven waarvan het patroon $$p$$ behoort tot $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$.
-
-
Bepaal als volgt de woorden $$w_1\ w_2\ w_3\ w_4$$ van een geheime boodschap:
-
het woord $$w_1$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_1 \cap \mathcal{P}_2$$
-
het woord $$w_2$$ staat op de unieke regel waarvan $$p$$ behoort tot $$ \mathcal{P}_2 \cap \mathcal{P}_3$$
-
het woord $$w_3$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_3 \cap \mathcal{P}_4$$
-
het woord $$w_4$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_4 \cap \mathcal{P}_1$$
Geef telkens een Unix commando waarin de reguliere expressies voor de verzamelingen $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$ gebruikt worden door commando's uit de grep familie om het woord $$w_j\ (j = 1, 2, 3, 4)$$ op te zoeken in het tekstbestand en uit te schrijven naar stdout. Hierbij is het niet toegelaten om het woord $$w_j$$ letterlijk uit te schrijven (bv. echo $$w_j$$).
-