Een curiositeit uit de jaren '30 die wordt toegeschreven aan professor E. Ducci.
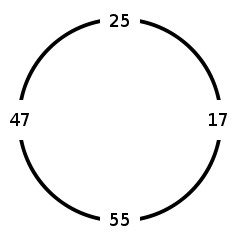
Plaats vier willekeurige gehele getallen in een cirkel, zoals aangegeven in bovenstaand voorbeeld. Bepaal nu een volgend getallenkwartet door het verschil te bepalen van alle opeenvolgende paren getallen, waarbij telkens het kleinste getal wordt afgetrokken van het grootste getal. Het kwartet uit bovenstaand voorbeeld levert op die manier het nieuwe getallenkwartet 22–8–38–8 op. Als we de procedure opnieuw toepassen op dit nieuwe kwartet, dan krijgen we het kwartet 14–30–30–14. Ducci ontdekte dat als we deze procedure blijven herhalen, we uiteindelijk altijd een kwartet van vier gelijke getallen bekomen. Een bewijs hiervan is terug te vinden in een artikel uit Ingenuity in Mathematics van Ross Honsberger (1970).
Invoer
Vier gehele getallen die elk op een afzonderlijke regel staan.
Uitvoer
We plaatsen de vier gegeven getallen in een cirkel, waarbij we het eerste getal uiterst links plaatsen en de opeenvolgende getallen in wijzerzin rond de cirkel plaatsen. Daarna passen we de procedure van Ducci toe, waarbij we het nieuwe kwartet opnieuw in een cirkel plaatsen. Daarbij is het getal uiterst links van de cirkel het verschil tussen de getallen links en boven in de oorspronkelijke cirkel, het getal bovenaan de nieuwe cirkel is het verschil tussen de getallen boven en rechts in de oorspronkelijke cirkel, en zo lopen we de cirkel verder in wijzerzin af.
Schrijf de opeenvolgende cirkels uit die je bekomt als je achtereenvolgens de procedure van Ducci toepast op de vier gegeven getallen. De eerste cirkel die je moet uitschrijven is de cirkel met de vier gegeven getallen, en de laatste cirkel die je moet uitschrijven is de eerste cirkel waarvan de vier getallen gelijk zijn. Elke cirkel wordt uitgeschreven op een afzonderlijke regel, waarbij de vier getallen achter elkaar worden uitgeschreven in de volgorde links–boven–rechts–onder en van elkaar worden gescheiden door koppeltekens (-).
Voorbeeld
Invoer:
47
25
17
55Uitvoer:
47-25-17-55
22-8-38-8
14-30-30-14
16-0-16-0
16-16-16-16