Klare tekst en cijfertekst zijn twee begrippen uit de cryptografie — Oudgrieks: κρυπτός (kruptós, "verborgen") en γράφειν (gráphein, "schrijven") — de toepassing en de studie van technieken waarmee een klare (leesbare) tekst kan versleuteld worden naar een onleesbare cijfertekst, die op zijn beurt terug kan ontsleuteld worden tot de oorspronkelijke klare tekst. De klare tekst is de oorspronkelijke (leesbare) tekst. De versleutelde (onleesbare) tekst heet de cijfertekst. De termen cijfertekst, vercijferen en ontcijferen zijn een beetje verwarrend, want de cijfertekst kan inderdaad uit cijfers bestaan, maar dat is niet per se het geval. Andere termen zijn coderen en decoderen, maar ook die zijn verwarrend omdat ze ook gebruikt worden voor codes die helemaal niet geheim zijn, zoals de Morsecode1.
De termen versleutelen (klare tekst omzetten naar cijfertekst) en ontsleutelen (cijfertekst omzetten naar klare tekst) hebben binnen de cryptografie een duidelijke betekenis. Ze verwijzen naar het feit dat er bij het versleutelen en ontsleutelen vaak een sleutel moet gebruikt worden: een extra stuk (geheime) informatie dat je nodig hebt om die acties te kunnen uitvoeren.
Opgave
Het Bernina-cijfer is een cryptografische techniek waarbij de sleutel en de cijfertekst even lang zijn (uit evenveel karakters bestaan). De cijfertekst wordt ontsleuteld door de sleutel boven de cijfertekst te zetten. Als voorbeeld gebruiken we deze sleutel en cijfertekst:
sleutel: π = 3.14159265358979323846264338327950288419716939 cijfertekst: BR7Ih4h a aideipoor rfi1tes0ir s fdgWtin0te rt?
Eerst lezen we de cijfertekst van links naar rechts, op zoek naar alle karakters die onder een cijfer 0 in de sleutel staan. In ons voorbeeld is dit enkel het geval voor de hoofdletter W. Daarna lezen we de cijfertekst van links naar rechts, op zoek naar alle karakters die onder een cijfer 1 in de sleutel staan. In ons voorbeeld zijn dat de letters h, a, t en een spatie. We herhalen deze procedure voor de cijfers 2–9:
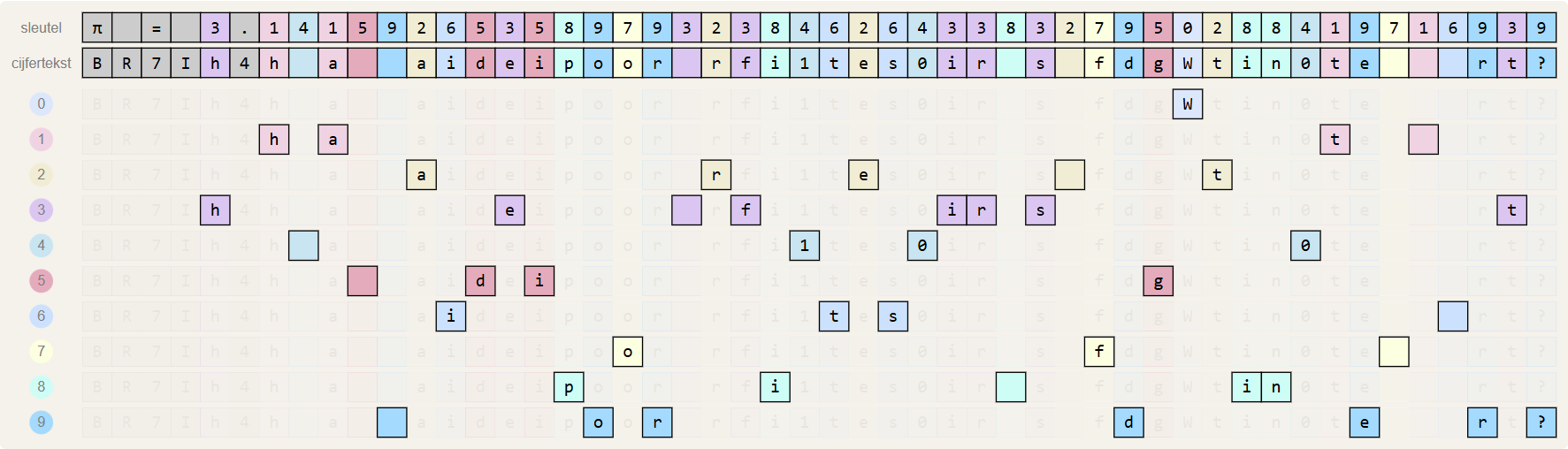
De klare tekst bekomen je door al deze karakters achter elkaar te zetten. Voor ons voorbeeld krijgen we:
011112222233333333444455556666777888889999999 klare tekst: What are the first 100 digits of pi in order?
Hierbij hebben we boven elk karakter van de klare tekst telkens het corresponderende cijfer uit de sleutel gezet. Merk op dat alle karakters uit de cijfertekst die niet onder een cijfer van de sleutel staan, door het Bernina-cijfer niet gebruikt worden om de klare tekst te vormen. Daardoor kan de klare tekst korter zijn dan de cijfertekst en de sleutel. We hebben deze karakters in het grijs weergegeven in bovenstaande figuur.
Invoer
De eerste regel bevat een sleutel en de tweede een cijfertekst die versleuteld werd op basis van het Bernina-cijfer met de gegeven sleutel. Beide regels bevatten evenveel karakters.
Uitvoer
De klare tekst die je bekomt door de cijfertekst te ontsleutelen met de gegeven sleutel.
Voorbeeld
Invoer:
π = 3.14159265358979323846264338327950288419716939
BR7Ih4h a aideipoor rfi1tes0ir s fdgWtin0te rt?Uitvoer:
What are the first 100 digits of pi in order?Epiloog
Ten zuiden van Brusio2 — in het Zwitserse kanton Graubünden3 — moet de Berninabahn4 van hoogte veranderen zonder de voorgeschreven maximale hellingsgraad van 7% te overschrijden. Dus kozen de ingenieurs voor de attractieve uitweg van een spiraalvormige viaduct: een boogbrug met negen overspanningen die een trein 360 graden vervoert met een helling die zacht genoeg is om de veiligheid te garanderen. De brug werd geopend in 1908 en werd in 2008 erkend als UNESCO Werelderfgoed5.

De naam van het Bernina-cijfer is een verwijzing naar deze ingenieuze oplossing, omdat je bij het ontsleutelen verschillende keren door de cijfertekst moet lopen om telkens de karakters te selecteren die in de sleutel corresponderen met het volgende cijfer.