We hebben lineaire interpolatie reeds in een vorige opgave¹ toegepast om ontbrekende meetresultaten van een functie $$y = f(x)$$ te schatten op basis van gekende metingen. We hadden daarbij de veronderstelling gemaakt dat de functie werd gemeten bij de $$x$$-waarden 1, 2, …, 100.

In deze opgave zullen we deze techniek uitbreiden voor een variabel aantal meetpunten $$x_i$$ ($$1 \leq i \leq n$$) die niet noodzakelijk samenvallen met de natuurlijke getallen, en die zelfs niet langer even ver van elkaar moeten liggen. Het enige wat we veronderstellen is dat er steeds geldt dat $$x_i < x_j$$ indien $$i < j$$, of met andere woorden dat er gemeten werd voor stijgende $$x$$-waarden (of dat de metingen in die volgorde gesorteerd werden).

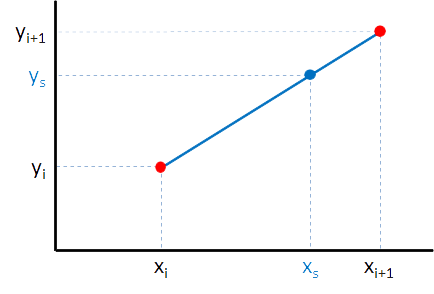
Om de waarde $$y_s = f(x_s)$$  te schatten die hoort bij een $$x$$-waarde $$x_s$$ — die tussen twee opeenvolgende $$x$$-waarden $$x_i$$ en $$x_{i+1}$$ in ligt — maken we nog steeds gebruik van de formule voor lineaire interpolatie: \[ y_s = y_i + (x_s-x_i)\frac{(y_{i+1}-y_i)}{(x_{i+1}-x_i)} \]

Opgave

Schrijf een functie interpolatie waaraan twee argumenten moeten doorgegeven worden. Het eerste argument is een lijst van meetpunten, waarbij elk meetpunt wordt voorgesteld als een tuple $$(x, y)$$ waarbij $$x, y \in \mathbb{R}$$. Het tweede argument is een getal $$x_s \in \mathbb{R}$$. Indien de $$x$$-waarden van de gegeven meetpunten niet in stijgende volgorde gegeven zijn, dan moet de functie de string 'ongeldige invoer' als resultaat teruggeven. Indien de gegeven $$x$$-waarde $$x_s$$ niet binnen het het bereik van de meetpunten ligt ($$x_s < x_1$$ of $$x_s > x_n$$), dan moet de functie de string 'buiten bereik' als resultaat teruggeven. Anders moet de functie als resultaat de $$y$$-waarde $$y_s \in \mathbb{R}$$ teruggeven die volgens het principe van de lineaire interpolatie correspondeert met de gegeven $$x$$-waarde $$x_s$$. 

Voorbeeld

>>> interpolatie([(4.88, -2.15), (6.42, -0.45), (6.99, 3.93), (7.69, -3.64)], 5.45)
-1.5207792207792203
>>> interpolatie([(3.3, 1.26), (4.25, -0.27), (6.17, 3.53), (8.16, 2.47)], 8.11)
2.496633165829146
>>> interpolatie([(2.24, 1.66), (3.5, 0.43), (3.96, -0.57), (4.35, -0.25)], 5.56)
'buiten bereik'
>>> interpolatie([(2.61, -1.97), (1.66, -0.05), (3.33, -0.93), (5.18, -0.58)], 7.1)
'ongeldige invoer'