Genoomassemblage is het computationele proces waarbij de genoomsequentie van een organisme bepaald wordt. Onderzoekers zijn momenteel nog niet in staat om de nucleotiden van een volledig genoom in één keer te bepalen. In plaats daarvan doen ze een beroep op hoogtechnologische chemische methoden om de basenvolgorde te bepalen van korte stukjes DNA (doorgaans minder dan 1000 bp lang). Deze korte stukjes worden de reads genoemd.
Om een volledig genoom te sequeneren, gaan onderzoekers verschillende kopieën van het genoom als het ware chemisch opblazen, waardoor elk van de bekomen reads door een sequenator kan uitgelezen worden. Om het genoom terug te reconstrueren, wordt gebruik gemaakt van de overlap tussen de reads om te bepalen welke reads naast elkaar op het genoom liggen. Als bijvoorbeeld de korte reads GACCTACA en ACCTACAA uitgelezen worden, dan kunnen we uit het feit dat ze overlappen, afleiden dat beide afkomstig zijn van het DNA fragment GACCTACAA.
Opgave
Als eerste stap bij genoomassemblage brengen de meeste algoritmen de overlappende reads in kaart door een overlapgraaf op te bouwen. Dit is een datastructuur waarbij overlappende reads (in onderstaande afbeelding voorgesteld door gelabelde cirkels) met elkaar worden verbonden door een pijl. Merk op dat het soms kan voorvallen dat een read overlapt met meerdere andere reads, vaak als gevolg van herhalingen in het genoom of fouten bij het uitlezen van de reads. Hierdoor ontstaan zogenaamde "vorken" in de overlapgraaf.
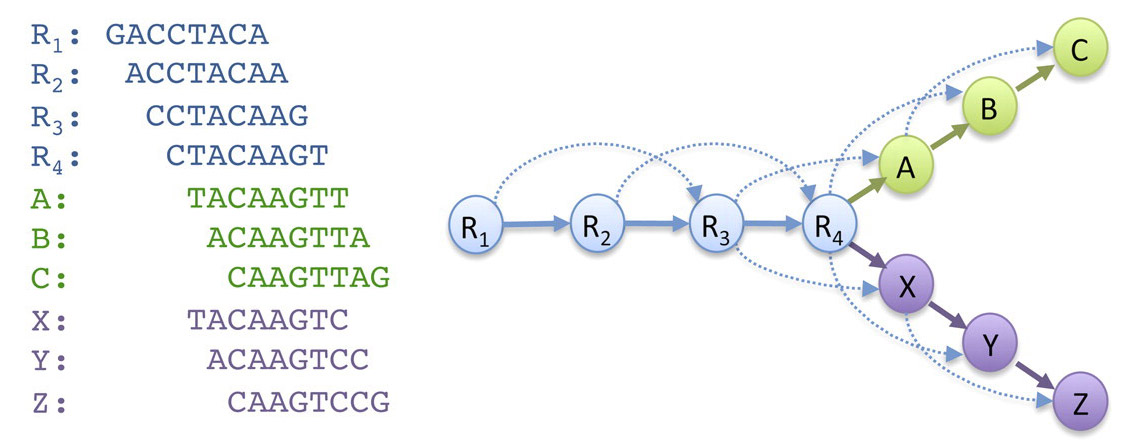
Het doel van deze opgave is dat je voor een gegeven verzameling reads zelf een overlapgraaf opbouwt. Hiervoor ga je als volgt te werk:
Schrijf een functie overlap waaraan drie argumenten moeten doorgegeven worden. De eerste twee argumenten zijn reads die voorgesteld worden als strings die enkel de letters A, C, G en T bevatten (deze stellen de vier mogelijke basen voor). Het derde argument is een getal $$k \in \mathbb{N}_0$$. De functie moet een Booleaanse waarde teruggeven, die aangeeft of de eerste read een overlap van lengte $$k$$ heeft met de tweede read. Dat is het geval als de laatste $$k$$ basen van de eerste read gelijk zijn aan de eerste $$k$$ basen van de tweede read.
Gebruik de functie overlap om een functie maximaleOverlap te schrijven. Aan deze functie moeten twee reads doorgegeven worden. De functie moet de lengte van de maximale overlap tussen de eerste en de tweede read teruggeven. Indien beide reads totaal niet overlappen, dan moet de waarde nul teruggegeven worden.
Gebruik de functie maximaleOverlap om een functie overlapgraaf te schrijven. Aan deze functie moeten twee argumenten doorgegeven worden: een collectie (een lijst, tuple, verzameling, …) van reads en een getal $$k \in \mathbb{N}_0$$. De functie moet een dictionary teruggeven, waarin elke read uit de gegeven collectie wordt afgebeeld op de verzameling van alle andere reads uit de collectie die ermee overlappen met lengte minstens $$k$$ (indien deze verzameling niet leeg is). Een dergelijke afbeelding stelt dus de pijlen uit de overlapgraaf voor die vertrekken vanuit een read (die als sleutel gebruikt in de dictionary) naar alle andere reads die ermee overlappen. Merk dus op dat er per definitie nooit een pijl getrokken wordt tussen een read en zichzelf, ook al zou die read met zichzelf overlappen.
Voorbeeld
>>> overlap('AAATTTT', 'TTTTCCC', 3)
True
>>> overlap('AAATTTT', 'TTTTCCC', 5)
False
>>> overlap('ATATATATAT', 'TATATATATA', 4)
False
>>> overlap('ATATATATAT', 'TATATATATA', 5)
True
>>> maximaleOverlap('AAATTTT', 'TTTTCCC')
4
>>> maximaleOverlap('ATATATATAT', 'TATATATATA')
9
>>> reads = ['AAATAAA', 'AAATTTT', 'TTTTCCC', 'AAATCCC', 'GGGTGGG']
>>> overlapgraaf(reads, 3)
{'AAATTTT': {'TTTTCCC'}, 'AAATAAA': {'AAATTTT', 'AAATCCC'}}
>>> overlapgraaf(reads, 4)
{'AAATTTT': {'TTTTCCC'}}
>>> reads = ['GACCTACA', 'ACCTACAA', 'CCTACAAG', 'CTACAAGT', 'TACAAGTT', 'ACAAGTTA', 'CAAGTTAG', 'TACAAGTC', 'ACAAGTCC', 'CAAGTCCG']
>>> overlapgraaf(reads, 6)
{'CTACAAGT': {'ACAAGTCC', 'ACAAGTTA', 'TACAAGTC', 'TACAAGTT'}, 'TACAAGTT': {'CAAGTTAG', 'ACAAGTTA'}, 'ACCTACAA': {'CTACAAGT', 'CCTACAAG'}, 'ACAAGTCC': {'CAAGTCCG'}, 'ACAAGTTA': {'CAAGTTAG'}, 'GACCTACA': {'CCTACAAG', 'ACCTACAA'}, 'TACAAGTC': {'ACAAGTCC', 'CAAGTCCG'}, 'CCTACAAG': {'CTACAAGT', 'TACAAGTC', 'TACAAGTT'}}
Opmerking: het laatste voorbeeld bouwt de overlapgraaf op die hierboven grafisch wordt weergegeven.