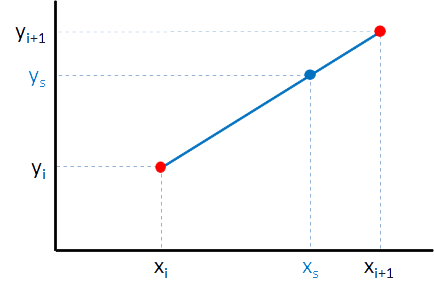
We beschikken over een tabel, waarvan de gegevens de $$y$$-waarden voor een bepaalde meting voorstellen. Daarin staan de meetresultaten die horen bij de $$x$$-waarden 1, 2, 3,…, 100. Om te schatten wat het resultaat $$y_s$$ is dat hoort bij een $$x$$-waarde $$x_s$$ — die tussen twee opeenvolgende gehele $$x$$-waarden $$x_i$$ en $$x_{i+1}$$ in ligt — maken we gebruik van de formule voor lineaire interpolatie: \[ y_s = y_i + (x_s-x_i)\frac{(y_{i+1}-y_i)}{(x_{i+1}-x_i)} \]

voorbeeld van lineaire interpolatie

opgave

Schrijf een functie lineaireInterpolatie die twee argumenten neemt. Het eerste argument moet een lijst met 100 getallen zijn en het tweede argument moet een float zijn tussen 1 en 100. De lijst stelt de $$y$$-waarden voor die horen bij de $$x$$-waarden $$1, 2, \ldots, 100$$. De functie geeft de $$y$$-waarde terug die correspondeert met de $$x$$-waarde die gegeven wordt door het tweede argument. Indien de argumenten niet aan de juiste voorwaarden voldoen, dan wordt een foutboodschap afgedrukt en de waarde None wordt teruggegeven. Bekijk het onderstaande voorbeeld om deze foutboodschappen te achterhalen.

Voorbeeld

>>> lineaireInterpolatie(list(range(1, 101)), 10.75)
10.75
>>> lineaireInterpolatie(list(range(1, 101))[::-1], 10.75)
90.25
>>> lineaireInterpolatie([42] * 100, 10.75)
42.0
>>> lineaireInterpolatie(42, 10.75)
Verwachte type: <class 'list'>, Ontvangen type: <class 'int'>
>>> lineaireInterpolatie(42, 0)
Verwachte type: <class 'list'>, Ontvangen type: <class 'int'>
>>> lineaireInterpolatie([42], 10)
Verwachte type: <class 'float'>, Ontvangen type: <class 'int'>
>>> lineaireInterpolatie([42], 10.75)
Verwachte lengte: 100, Ontvangen lengte: 1
>>> lineaireInterpolatie([42] * 100, 100.75)
Interpolatie is enkel mogelijk voor waarden van 1 tot en met 100.