Snelheid van het doel bepalen

Buiten de afstand tot het doel is het ook belangrijk om de snelheid van het doel te kennen. De hoofbatterij, dat zijn de grootste kannonnen, van Bismarck konden een granaat van 800kg maximaal 36 520m ver schieten. De granaat had een beginsnelheid van 820m/s. Hoewel de snelheid van de granaat hoog is, is de tijd die de granaat nodig heeft om het doel te bereiken toch nog steeds 44 seconden. In die tijd kan het doel zich verplaatsen. Het is dus belangrijk om de snelheid van het doel te kennen.

Hoe bepalen we de snelheid van het doel?

Het bepalen van de snelheid van het doel is een moeilijke opdracht. De snelheid van het doel is niet constant. Het doel kan versnellen of vertragen, onze eigen snelheid kan veranderen, etc…

Om deze opdracht haalbaar te houden gaan we uit van de volgende vereenvoudigde situatie:

Het doel beweegt met een constante snelheid.
Ons eigen schip beweegt niet.
De snelheid van het doel is niet gekend.

Hoe bepalen we de snelheid van het doel?

Opnieuw kunnen we gebruik maken van de driehoecksmeetkunde. We gaan de snelheid van het doel bepalen door de afstand tot het doel te meten op verschillende tijdstippen en hierbij ook te noteren onder welke hoek we het doel zien.

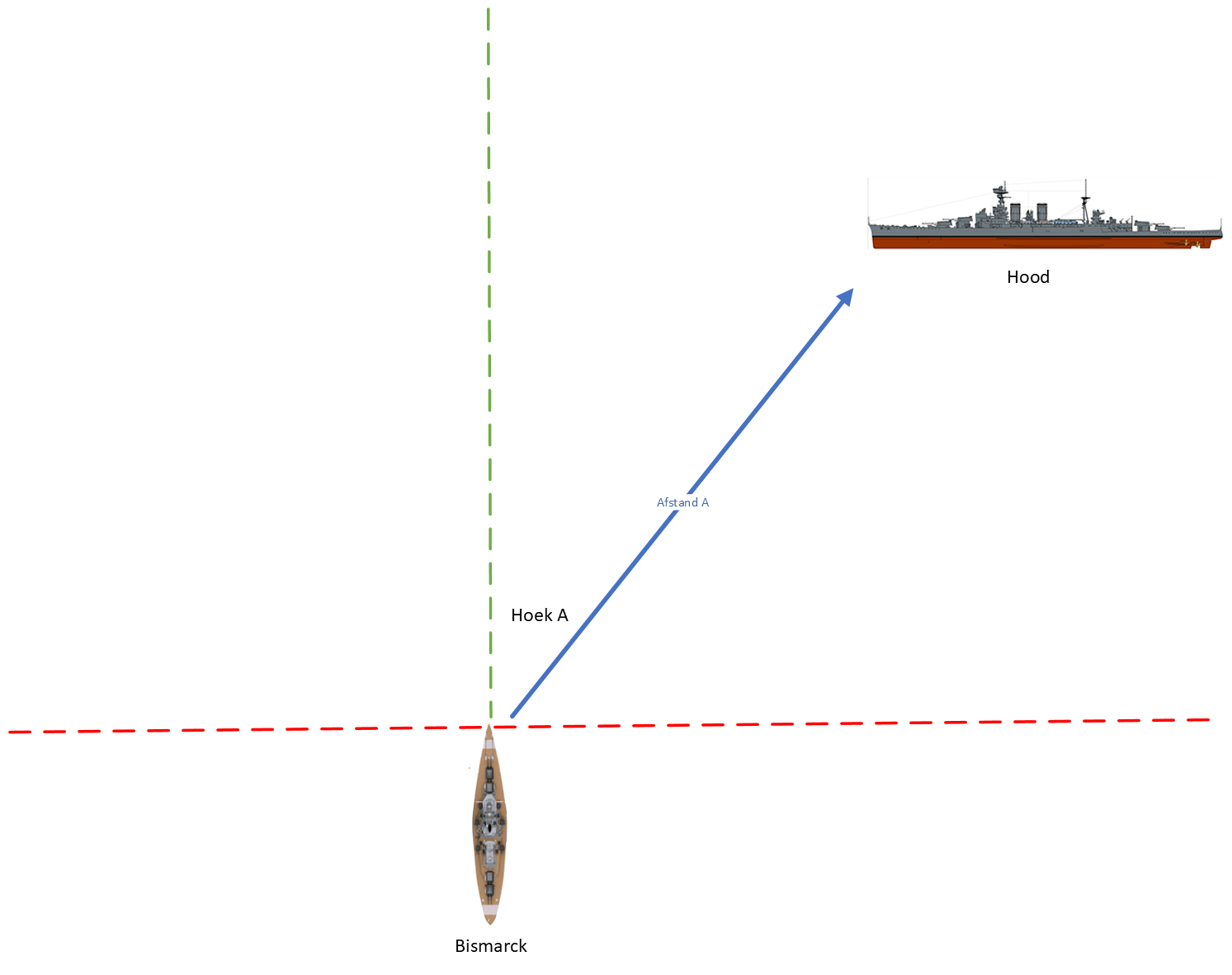De beginsituatie Beginsituatie

In de schets hierboven zie je de beginsituatie. Dankzij de rangefinder kunnen we de afstand tot het doel bepalen, in de schets voorgesteld door de zij A. We weten ook onder welke hoek we het doel zien. We noteren de hoek als \(\alpha\) en de afstand als \(A\), hierbij noteren we ook de tijd \(t_0\).

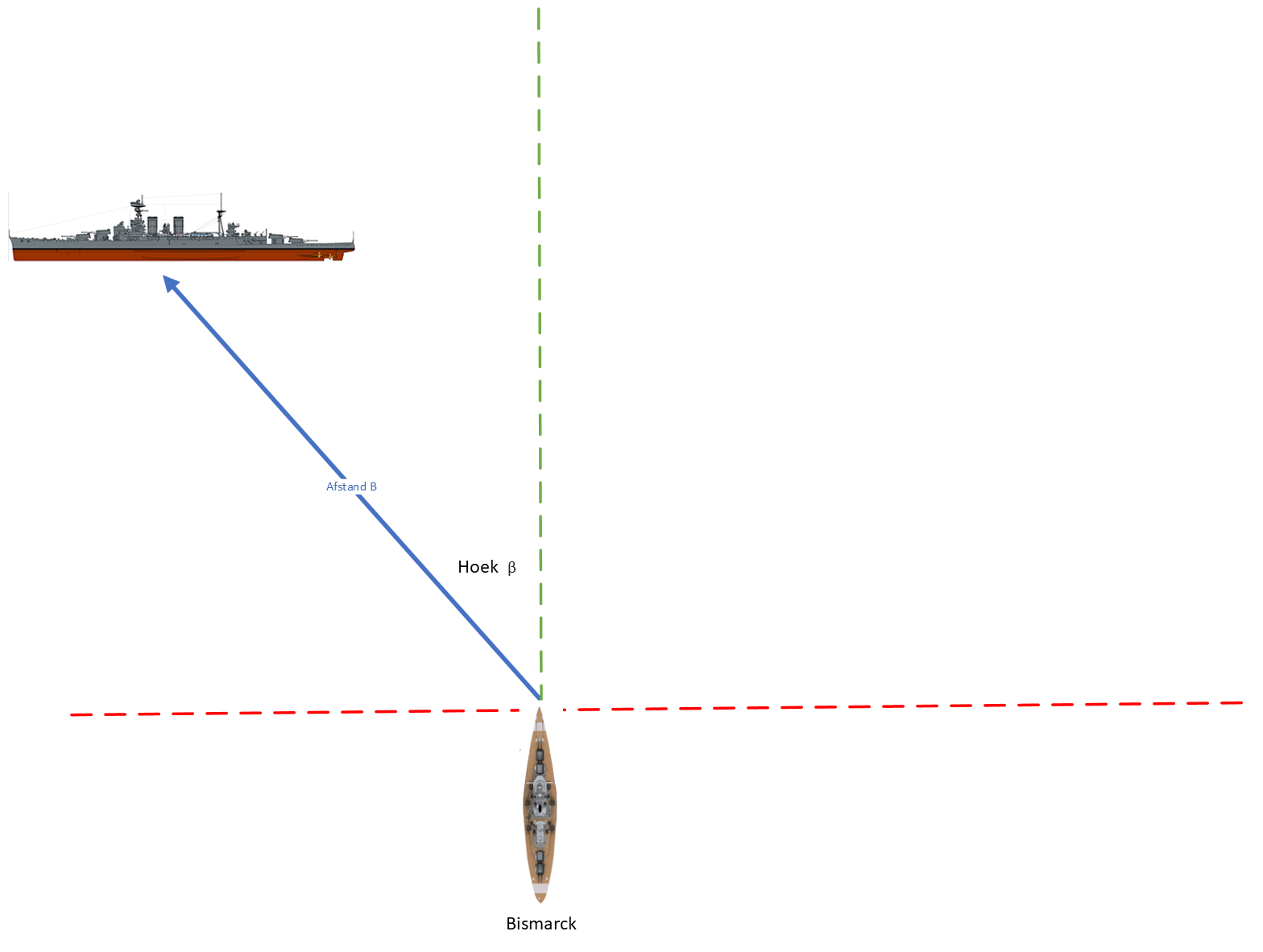De situatie na enige tijd Situatie na enige tijd

Na enige tijd meten we opnieuw de afstand tot het doel, in de schets voorgesteld door zijde B. We noteren de hoek als \(\beta\) en de afstand als \(B\), hierbij noteren we ook de tijd \(t_1\).

De situatie na enige tijd Afstand C kan nu bepaald worden

Formule voor de afgelegde afstand

Zoals je kan zien hebben we te maken met een driehoek waarvan we de lengte van twee zijden kennen en de hoek tussen deze twee zijden (deze is gelijk aan de som van hoek \(\alpha\) en \(\beta\) ). We kunnen de lengte van de derde zijde bepalen met behulp van de cosinusregel.

De cosinusregel zegt dat:

\[C^2 = A^2 + B^2 - 2AB\cos(\alpha + \beta)\]

Om de lengte van C te bepalen herschrijven we deze formule tot:

\[C = \sqrt{A^2 + B^2 - 2AB\cos(\alpha + \beta)}\]

Formule voor de snelheid

Nu we de afstand C kunnen bepalen kunnen we ook de snelheid van het doel bepalen. De snelheid is gelijk aan de afstand gedeeld door de tijd.

We hebben bij beide metingen ook de tijd genoteerd. De snelheid is dus gelijk aan:

\[v_{\frac{m}{s}} = \frac{C}{t_1 - t_0}\]

Omdat de afstand werd bepaald in meter zal de afstand ook in meter zijn. De tijd werd genoteerd in seconden. De snelheid zal dus uitgedrukt worden in meter per seconde.

Echter werkt men in de scheepvaart niet met meter per seconde maar met knopen. 1 knoop is gelijk aan 1 zeemijl per uur. 1 zeemijl is gelijk aan 1852 meter.

Om de snelheid uit te drukken in knopen moeten we de snelheid dus nog delen door 1852 en vermenigvuldigen met 3600.

\[v_{knopen} = \frac{C}{t_1 - t_0} \cdot \frac{3600}{1852}\]

Opdracht

Je bouwt een console-applicatie die de snelheid van het doel bepaalt aan de hand van de volgende gegevens:

De afstand tot het doel op tijdstip \(t_0\) in meter
De hoek \(\alpha\) op tijdstip \(t_0\) in graden
De afstand tot het doel op tijdstip \(t_1\) in meter
De hoek \(\beta\) op tijdstip \(t_1\) in graden
Jouw applicatie berekent de afgelede afstand C in meter. Afgerond op 1 meter.
Jouw applicatie berekent de snelheid van het doel in knopen. Afgerond op 0,1 knopen.

Stappenplan

Vraag de gebruiker om de afstand tot het doel op tijdstip \(t_0\) in meter in te geven. Omdat de rangefinders uit WOII niet zo nauwkeurig waren mag je er vanuit gaan dat de afstand een geheel getal is.
Vraag de gebruiker vervolgens om de hoek \(\alpha\) op tijdstip \(t_0\) in graden in te geven. Deze hoek kan wel een kommagetal zijn.
Vraag de gebruiker om de datum en tijd in te geven van tijdstip \(t_0\).
Vraag de gebruiker om de afstand tot het doel op tijdstip \(t_1\) in meter in te geven. Ook nu verwachten we een geheel getal
Vraag de gebruiker om de hoek \(\beta\) op tijdstip \(t_1\) in graden in te geven. Deze hoek kan wel een kommagetal zijn.
Vraag de gebruiker om de datum en tijd in te geven van tijdstip \(t_1\).

Eens je deze gegevens hebt kan het echte werk beginnen.

Bereken de afstand C met behulp van de cosinusregel.

Om de afstand C te bepalen zal je al jouw kennis over operatoren en de Math-library moeten gebruiken. Dit is een complexe opdracht. Ga er dus niet vanuit dat je deze opdracht in 1 keer zal kunnen oplossen. Probeer eerst een deel van de oplossing te vinden en bouw van daaruit verder.

Je kan een Sandbox gebruiken om jouw oplossing te testen. Hieronder vindt je een tabel met enkele waarden die je kan gebruiken om jouw oplossing te testen.

A	B	\(\alpha\)	\(\beta\)	C
4500	6000	30	30	~5408
8000	12 000	30	70	~15535
21 083	28 038	60	15	~30408

Hoeken omzetten naar radialen

Zoals je in eerdere oefeningen al zag werken de trigonometrische functies van de Math klasse met radialen. De hoeken die we hier gebruiken zijn echter in graden. Je zal de hoeken dus eerst moeten omzetten naar radialen. Om een hoek in graden om te zetten naar radialen kan je de volgende formule gebruiken:

double hoekInGraden = 45;
double hoekInRadialen = hoekInGraden * Math.PI / 180;

Tip

In de Math library zit een functie om de vierkantswortel te berekenen. Aan jou om deze te vinden.

Bereken de snelheid van het doel in knopen

Nu je de afstand C hebt berekend kan je de snelheid van het doel berekenen. De snelheid is gelijk aan de afstand gedeeld door de tijd. De tijd is gelijk aan het verschil tussen tijdstip \(t_1\) en tijdstip \(t_0\).

We gaan er wel van uit dat de gebruiker een datum/tijd ingeeft vb: 2021-01-01 12:00:00. Je zal dus eerst de datum/tijd moeten omzetten naar een DateTime object.

Nadien kan je met de DateTime-library de tijd tussen \(t_1\) en \(t_0\) berekenen.

Bereken vervolgens de snelheid van het doel in meter per seconden. Rond de snelheid af op 1 meter per seconde.

\[v_{\frac{m}{s}} = \frac{C}{t_1 - t_0}\]

Als laatste stap moet je de snelheid nog omzetten naar knopen. Dit doe je door de snelheid te delen door 1852 en te vermenigvuldigen met 3600.

\[v_{knopen} = \frac{C}{t_1 - t_0} \cdot \frac{3600}{1852}\]

Rond de snelheid af op 0,1 knopen.

Toon de resultaten op het scherm

csharp

Wat is de afstand tot het doel op tijdstip t0 in meter?
[invoer]
Wat is de hoek a op tijdstip t0 in graden?
[invoer]
Wat is de datum en tijd van tijdstip t0? 
[invoer]
Wat is de afstand tot het doel op tijdstip t1 in meter?
[invoer]
Wat is de hoek b op tijdstip t1 in graden?
[invoer]
Wat is de datum en tijd van tijdstip t1?
De afgelegde afstand van het doel is: [uitvoer] meter.
De snelheid van het doel is: [uitvoer] m/s.
De snelheid van het doel is: [uitvoer] knopen.

Voorbeeldoplossingen

Hieronder een tabel met voorbeeldoplossingen. Deze oplossingen zijn niet de enige juiste oplossingen.

TEST	A	B	\(\alpha\)	\(\beta\)	C	\(t_0\)	\(t_1\)	Snelheid in m/s	Snelheid in knopen
1	4500	6000	30	30	5408	24/05/1941 06:00	24/05/1941 06:09	10	19,4
2	8000	12000	30	70	15535	24/05/1941 06:00	24/05/1941 06:28	9	17.5