Lying in wait

Single gene disorders can be encoded by either dominant or recessive alleles. In the latter case, the affected person usually has two healthy carrier parents, who were usually unaware that their child could inherit a deadly or debilitating genetic condition from them.

We know from Mendel's first law that any offspring of two heterozygous carriers has a 25% chance of inheriting a recessive disorder. Knowing your own genotype is therefore important when deciding to have children, and genetic screening will prove vital for preventive medicine in the coming years.

In this assignment, we will consider an exercise in which we determine the probability of an organism exhibiting each possible genotype for a factor knowing only the genotypes of the organism's ancestors.

Assignment

A rooted binary tree can be used to model the pedigree of an individual. In this case, rather than time progressing from the root to the leaves, the tree is viewed upside down with time progressing from an individual's ancestors (at the leaves) to the individual (at the root).

An example of a pedigree for a single factor in which only the genotypes of ancestors are given is shown in the figure below.

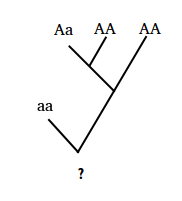
Write a function probabilities that takes a rooted binary tree $$T$$ in Newick format, encoding an individual's pedigree for a Mendelian factor whose alleles are A (dominant) and a (recessive). The function must return a dictionary whose keys are the genotypes AA, Aa and aa. The dictionary maps each of these genotypes to a floating point number between 0 and 1, corresponding to the probability that the individual at the root of $$T$$ will exhibit that genotype.

Example

>>> probabilities('((((Aa,aa),(Aa,Aa)),((aa,aa),(aa,AA))),Aa)')
{'AA': 0.156, 'Aa': 0.5, 'aa': 0.344}