De sestina is een dichtvorm waarbij aan zeer strikte voorwaarden moet voldaan worden. Een sestina bestaat immers uit zes stanza's (verzen) van zes regels, waarbij elk stanza eindigt op dezelfde zes woorden die volgens een vast patroon gepermuteerd worden.

Grafische voorstelling van het algoritme dat gebruikt worden voor het rangschikken van de eindwoorden van een sestina.

Een sestina kan eventueel nog afgesloten worden door een envoi: een zevende stanza van drie regels. Sinds de twaalfde eeuw heeft dit intrigerende strakke keurslijf menig dichter geïnspireerd. John Frederick Nims omschreef de dichtvorm op de volgende manier:

In een goede sestina spoken zes woorden, zes beelden, zes ideeën zo hard door het hoofd van de dichter dat hij er moeilijk aan kan ontsnappen. Hij wil ze in alle mogelijke combinaties wringen om te achterhalen hoe ze met elkaar verbonden zijn.

De oudste bekende sestina is Lo ferm voler qu'el cor m'intra die rond 1200 werd geschreven door Arnaut Daniel, een troubadour uit de streek van Aquitanië (Frankrijk). Hij wordt dan ook aanzien als de uitvinder van de dichtvorm die hij zelf benoemde met de Occitaanse term cledisat, wat min of meer dezelfde betekenis heeft als "verweven".

De oudste bekende sestina Lo ferm voler qu'el cor m'intra die rond 1200 in het Occitaans werd geschreven door Arnaut Daniel.

Opgave

In een sestina speelt het getal zes een voorname rol. Voor deze opgave vragen we je om te controleren of een gegeven gedicht — waarvan de tekst is opgeslagen in een tekstbestand — voldoet aan een reeks zeer strikte voorwaarden die sterk lijken op de voorwaarden van een sestina. We zullen ons echter niet vastpinnen op het getal zes, maar de voorwaarden algemener formuleren in functie van een getal $$n \in \mathbb{N}_0$$. Voor we komen tot een oplijsting van de voorwaarden, moeten we eerst nog een aantal andere dingen vastleggen.

Een gedicht bestaat uit een aantal stanza's die elk bestaan uit een aantal opeenvolgende regels tekst en van elkaar worden gescheiden door minstens één lege regel. Een lege regel is een regel die enkel witruimtekarakters bevat (spaties, tabs en/of newlines). Ook vóór het eerste stanza en na het laatste stanza kunnen lege regels voorkomen. De woorden van het gedicht worden gevormd door de langst mogelijke opeenvolging van letters. Elke regel van een stanza bevat minstens één woord, en het laatste woord van een regel wordt het eindwoord genoemd.

Een permutatie van een reeks van $$n$$ elementen is een reeks van $$n$$ elementen die volgt na herschikking van de elementen in de originele reeks. Een permutatie wordt voorgesteld door een lijst die de getallen 1 tot en met $$n$$ bevat, in een willekeurige volgorde. Zo stelt de lijst [6, 1, 5, 2, 4, 3] bijvoorbeeld de permutatie voor die eerst het zesde element bevat uit de originele reeks elementen, gevolgd door het eerste, het vijfde, het tweede, het vierde en het derde element van de originele reeks.

De canonieke permutatie van een reeks van $$n$$ elementen wordt bepaald aan de hand van de volgende procedure. Splits de $$n$$ elementen op in twee helften. Indien $$n$$ oneven is, dan bevat de tweede helft één element meer dan de eerste helft. Keer de volgorde van de elementen uit de tweede helft om, en plaats na elk van die elementen telkens het volgende element uit de eerste helft. Dit wordt hieronder geïllustreerd voor een even (links) en een oneven (rechts) aantal elementen. Deze canonieke permutatie is de standaard permutatie die gebruikt wordt voor het bepalen van de volgorde van de eindwoorden in een sestina (voor $$n = 6$$) en een pentina (voor $$n = 5$$).

De canonieke permutatie van zes elementen (links) zoals die standaard gebruikt wordt voor het bepalen van de volgorde van de eindwoorden in een sestina, en de canonieke permutatie van vijf elementen (rechts) zoals die standaard gebruikt wordt voor het bepalen van de volgorde van de eindwoorden in een pentina.

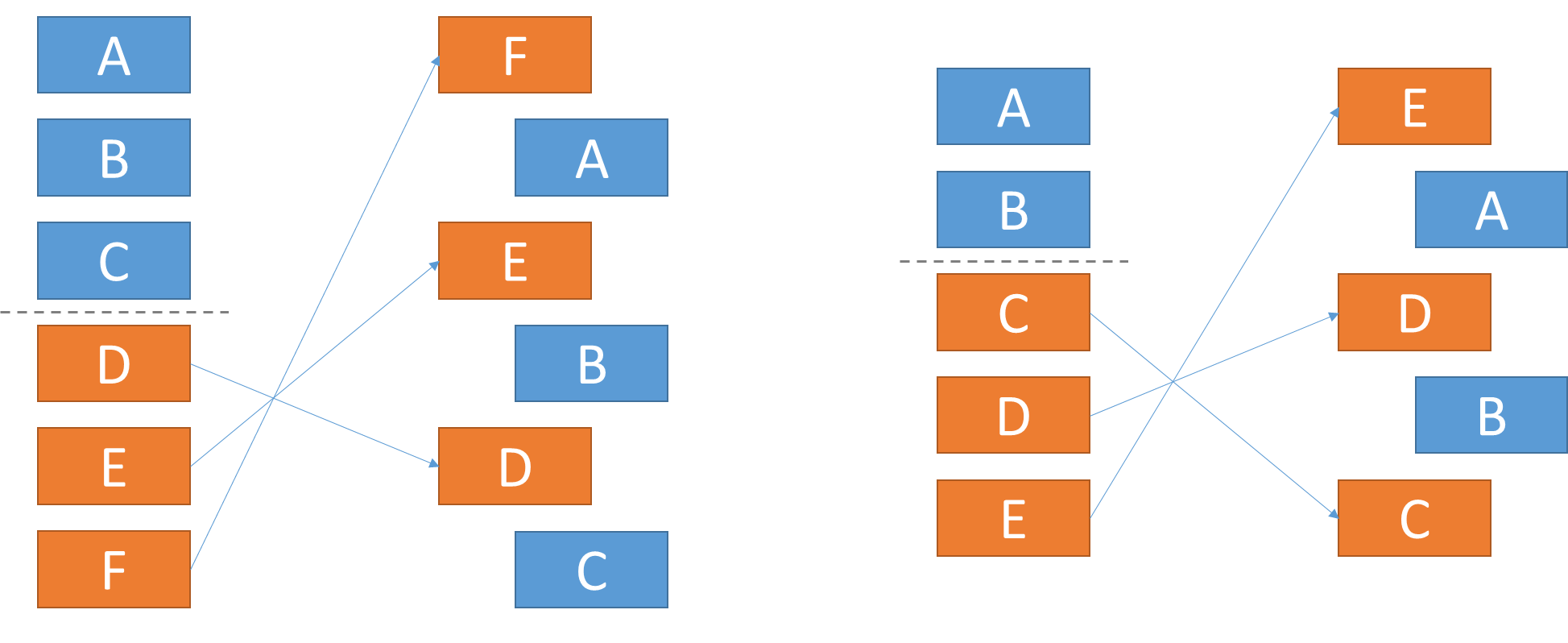
Voor een gegeven gedicht bepalen we $$n \in \mathbb{N}_0$$ als het aantal regels in het eerste stanza. De voorwaarden waaraan een sestina-achtig gedicht dan moet voldoen zijn:

het gedicht bestaat uit $$n$$ stanza's van elk $$n$$ regels, eventueel gevolgd door een extra stanza (het envoi) van $$\lfloor \frac{n}{2} \rfloor$$ regels; hierbij staat $$\lfloor x \rfloor \in \mathbb{N}$$ voor het geheel deel van $$x \in \mathbb{R}^{+}$$
toepassen van een gegeven permutatie op de eindwoorden van de eerste $$n - 1$$ stanza's levert telkens de volgorde op van de eindwoorden van het volgende stanza; bij het vergelijken van de eindwoorden mag geen onderscheid gemaakt worden tussen hoofdletters en kleine letters
de eindwoorden van het envoi (indien aanwezig) zijn ook eindwoorden van de andere stanza's; bij het vergelijken van de eindwoorden mag geen onderscheid gemaakt worden tussen hoofdletters en kleine letters; merk dus op dat er in tegenstelling tot de eerste $$n$$ stanza's geen voorwaarden opgelegd worden aan de volgorde waarin de eindwoorden voorkomen in het envoi

Om te controleren of een gegeven gedicht aan deze voorwaarden voldoet, gaan we als volgt te werk:

Schrijf een functie eindwoord waaraan een string moet doorgegeven worden. De functie moet het eindwoord van deze string teruggeven, en mag er daarbij van uitgaan dat de string minstens één woord bevat.
Schrijf een functie stanzas waaraan de locatie van een tekstbestand moet doorgegeven worden waarin de tekst van een gedicht zit opgeslagen. De functie moet een lijst teruggeven met de opeenvolgende stanza's van het gedicht. Hierbij wordt elk stanza voorgesteld door een lijst van eindwoorden van de opeenvolgende regels van het stanza. Alle eindwoorden moeten omgezet worden naar kleine letters.
Schrijf een functie permutatie waaraan een lijst van $$n \in \mathbb{N}_0$$ elementen moet doorgegeven worden. De functie heeft ook nog een tweede optionele parameter patroon waaraan een lijst van getallen kan doorgegeven worden, die een permutatie van een reeks van $$n$$ elementen moet voorstellen. De functie moet een nieuwe lijst teruggeven die de gegeven permutatie van de elementen in de gegeven lijst bevat. Indien de waarde die aan de parameter patroon wordt doorgegeven geen herschikking voorstelt van de getallen 1 tot en met $$n$$, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige permutatie. Indien niet expliciet een waarde wordt doorgegeven aan de parameter patroon, dan moet de functie de canonieke permutatie van de elementen in de gegeven lijst teruggeven.
Schrijf een functie sestina waaraan de locatie van een tekstbestand moet doorgegeven worden waarin de tekst van een gedicht zit opgeslagen. De functie heeft ook nog een tweede optionele parameter patroon die dezelfde betekenis heeft als bij de functie permutatie. De functie moet een Booleaanse waarde teruggeven die aangeeft of het gegeven gedicht voldoet aan alle voorwaarden die we hierboven hebben opgelegd aan een sestina-achtig gedicht. Bij het controleren van de tweede voorwaarde moet uiteraard gebruikgemaakt worden van de permutatie die omschreven wordt door het argument dat werd doorgegeven aan de parameter patroon.

Voorbeeld

Bij onderstaande voorbeeldsessie gaan we ervan uit dat de tekstbestanden sestina0.txt¹, sestina1.txt² en sestina2.txt³ zich in de huidige directory bevinden.

>>> eindwoord("Lo ferm voler qu'el cor m'intra")
'intra'
>>> eindwoord("no'm pot ges becs escoissendre ni ongla")
'ongla'
>>> eindwoord("de lauzengier qui pert per mal dir s'arma;")
'arma'

>>> stanzas('sestina0.txt')
[['intra', 'ongla', 'arma', 'verja', 'oncle', 'cambra'], ['cambra', 'intra', 'oncle', 'ongla', 'verja', 'arma'], ['arma', 'cambra', 'verja', 'intra', 'ongla', 'oncle'], ['oncle', 'arma', 'ongla', 'cambra', 'intra', 'verja'], ['verja', 'oncle', 'intra', 'arma', 'cambra', 'ongla'], ['ongla', 'verja', 'cambra', 'oncle', 'arma', 'intra'], ['oncle', 'arma', 'intra']]
>>> stanzas('sestina1.txt')
[['enters', 'nail', 'soul', 'rod', 'uncle', 'room'], ['room', 'enters', 'uncle', 'nail', 'rod', 'soul'], ['soul', 'room', 'rod', 'enters', 'nail', 'uncle'], ['uncle', 'soul', 'nail', 'room', 'enters', 'rod'], ['rod', 'uncle', 'enters', 'soul', 'room', 'nail'], ['nail', 'rod', 'room', 'uncle', 'soul', 'enters'], ['nail', 'soul', 'enters']]
>>> stanzas('sestina2.txt')
[['woe', 'sound', 'cryes', 'part', 'sleepe', 'augment'], ['augment', 'woe', 'sound', 'cryes', 'part', 'sleepe'], ['sleepe', 'augment', 'woe', 'sound', 'cryes', 'part'], ['part', 'sleepe', 'augment', 'woe', 'sound', 'cryes'], ['cryes', 'part', 'sleepe', 'augment', 'woe', 'sound'], ['sound', 'cryes', 'part', 'sleepe', 'augment', 'woe'], ['sound', 'part', 'augment']]

>>> permutatie(['rose', 'love', 'heart', 'sang', 'rhyme', 'woe'])
['woe', 'rose', 'rhyme', 'love', 'sang', 'heart']
>>> permutatie(['woe', 'rose', 'rhyme', 'love', 'sang', 'heart'])
['heart', 'woe', 'sang', 'rose', 'love', 'rhyme']
>>> permutatie(['rose', 'love', 'heart', 'sang', 'rhyme'])
['rhyme', 'rose', 'sang', 'love', 'heart']
>>> permutatie(['rose', 'love', 'heart', 'sang', 'rhyme', 'woe'], [6, 1, 5, 2, 4, 3])
['woe', 'rose', 'rhyme', 'love', 'sang', 'heart']
>>> permutatie(['rose', 'love', 'heart', 'sang', 'rhyme', 'woe'], [6, 5, 4, 3, 2, 1])
['woe', 'rhyme', 'sang', 'heart', 'love', 'rose']
>>> permutatie(['rose', 'love', 'heart', 'sang', 'rhyme', 'woe'], [6, 1, 5, 3, 4, 3])
Traceback (most recent call last):
AssertionError: ongeldige permutatie

>>> sestina('sestina0.txt')
True
>>> sestina('sestina0.txt', [6, 1, 5, 2, 4, 3])
True
>>> sestina('sestina1.txt')
True
>>> sestina('sestina2.txt')
False
>>> sestina('sestina2.txt', [6, 1, 2, 3, 4, 5])
True