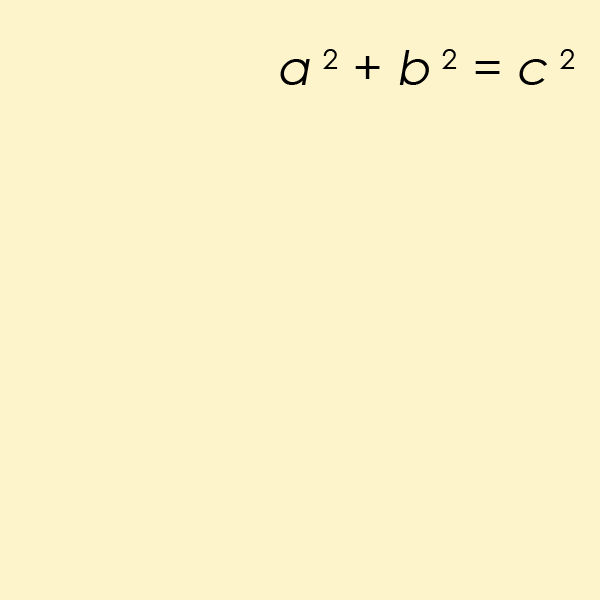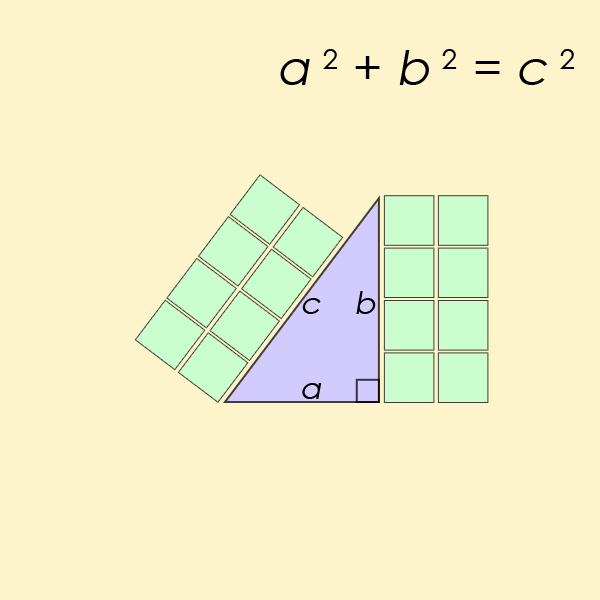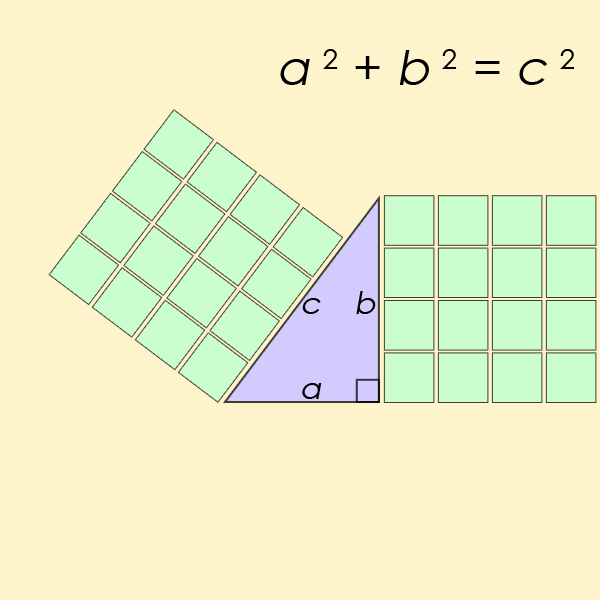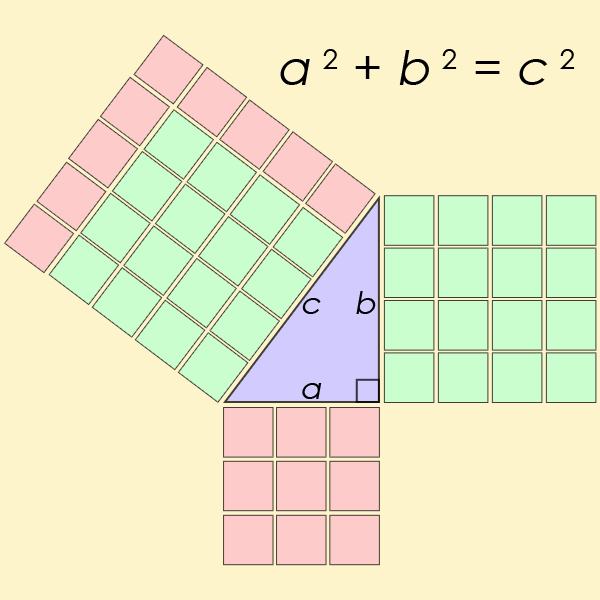Een Pythagorees drietal1 $$(a, b, c)$$ bestaat uit drie strikt positieve natuurlijke getallen $$a$$, $$b$$ en $$c$$ waarvoor geldt dat \[ a^2 + b^2 = c^2 \] De naam werd afgeleid van de stelling van Pythagoras2, aangezien dergelijke drietallen kunnen optreden als lengtes van de zijden van een rechthoekige driehoek met $$c$$ als lengte van de schuine zijde.
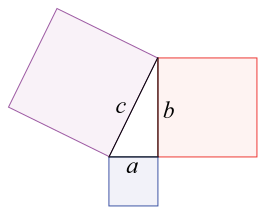
Naast het drietal $$(3, 4, 5)$$ vormen ook veelvouden hiervan, zoals $$(6, 8, 10)$$ en $$(9, 12, 15)$$ Pythagorese drietallen. Algemeen is met $$(a, b, c)$$ ook $$(ka, kb, kc)$$ voor elk positief natuurlijk getal $$k$$ een Pythagorees drietal. Een Pythagorees drietal $$(a, b, c)$$ wordt primitief genoemd als $$a$$, $$b$$ en $$c$$ geen andere delers dan 1 gemeen hebben. Er bestaan bijvoorbeeld vier Pythagorese drietallen $$(a, b, c)$$ waarvoor $$a + b + c = 240$$: $$(15, 112, 113)$$, $$(40, 96, 104)$$, $$(48, 90, 102)$$ en $$(60, 80, 100)$$.
Op kleitabletten uit de tijd van Hammurabi3 komen al Pythagorese drietallen voor. Het oudste voorbeeld hiervan is Plimpton 3224, een Babylonische kleitablet van rond 1800 voor Christus, geschreven in een zestigtallig stelsel. Het werd kort na 1900 ontdekt door Edgar James Banks5, en in 1922 voor $10 verkocht aan George Arthur Plimpton6. Op dit tablet staan 15 drietallen, waaronder $$(56, 90, 106)$$, $$(119, 120, 169)$$ en zelfs $$(12709, 13500, 18541)$$. Ook in India kende men al Pythagorese drietallen. In de Baudhayana-Sulbasutra7 uit de 6e eeuw voor Christus staan vijf zulke drietallen.
Invoer
Een getal $$n \in \mathbb{N}_0$$.
Uitvoer
Een lijst van alle Pythagorese drietallen $$(a, b, c)$$ waarvoor $$0 < a \leq b \leq c$$ en $$a + b + c = n$$. De drietallen moeten uitgeschreven worden onder de vorm (a, b, c), elk op een afzonderlijk regel en oplopend gesorteerd volgens $$a$$, dan $$b$$ en dan $$c$$.
Voorbeeld
Invoer:
240Uitvoer:
(15, 112, 113)
(40, 96, 104)
(48, 90, 102)
(60, 80, 100)