Verdeling van het steekproefgemiddelde

Om ondermeer goed de betekenis van de standard error te kunnen vatten, moeten we van \(\bar X\) niet alleen het gemiddelde en de standaarddeviatie, maar ook de exacte verdeling kennen. De standard error is immers een standaardeviatie (bvb. van het steekproefgemiddelde), waarvan de betekenis het meest duidelijk is wanneer de metingen (in dit geval, het steekproefgemiddelde) Normaal verdeeld zijn. In het bijzonder geval dat de individuele observaties \(X_i\) een Normale verdeling hebben met gemiddelde \(\mu\) en variantie \(\sigma^2\), kan men aantonen dat ook \(\bar X\) Normaal verdeeld is met gemiddelde \(\mu\) en variantie \(\sigma^2/n.\)

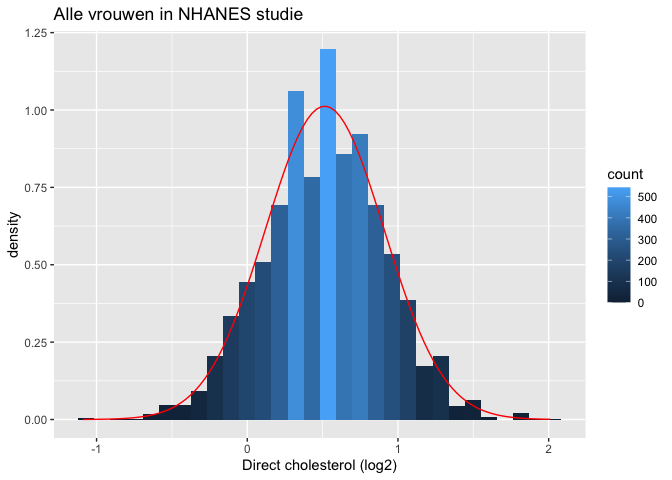
NHANES: cholesterol

We illustreren dit nogmaals met een simulatie gebruik makende van de NHANES-studie. De log2-cholesterolwaarden zijn normaal verdeeld.

 fem %>%
  ggplot(aes(x = DirectChol %>% log2))+
  geom_histogram(aes(y = ..density.., fill = ..count..)) +
  xlab("Direct cholesterol (log2)") +
  stat_function(
    fun = dnorm,
    color = "red",
    args = list(
      mean=mean(fem$DirectChol%>%log2),
      sd = sd(fem$DirectChol%>%log2)
      )
    ) +
  ggtitle("Alle vrouwen in NHANES studie")

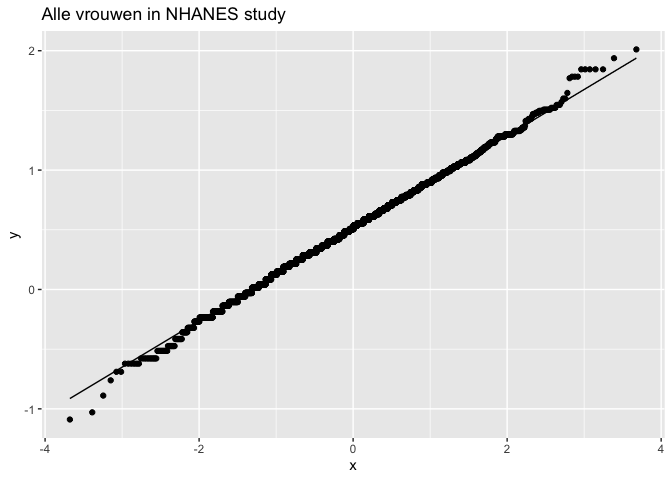
fem %>%
  ggplot(aes(sample = DirectChol %>% log2)) +
  stat_qq() +
  stat_qq_line() +
  ggtitle("Alle vrouwen in NHANES study")

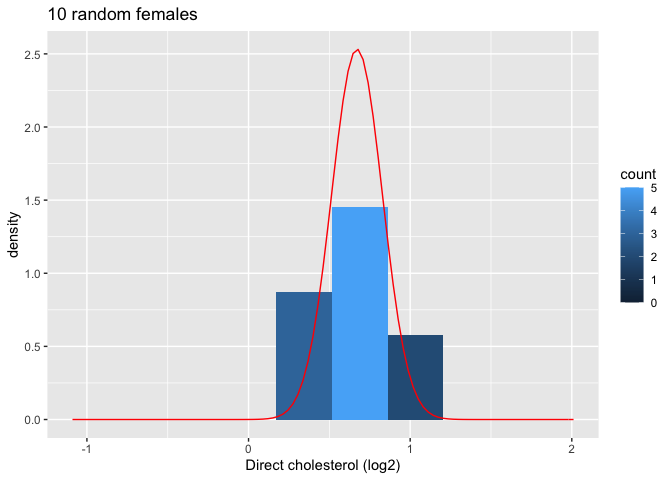
Evalueer de verdeling van het gemiddelde voor steekproeven van grootte 10

Nu onderzoeken we de resultaten voor de steekproefgrootte van 10.

We bekijken eerst de plot voor de eerste steekproef.

femSamp10[,1] %>%
  log2 %>%
  as.data.frame %>%
  ggplot(aes(x=.))+
    geom_histogram(aes(y=..density.., fill=..count..),bins=10) +
    xlab("Direct cholesterol (log2)") +
    stat_function(
      fun=dnorm,
      color="red",
      args=list(
        mean=femSamp10[,1]%>%log2%>%mean, sd=femSamp10[,1]%>%log2%>%sd)
      ) +
    ggtitle("10 random females") +
    xlim(fem$DirectChol %>% log2 %>% range)

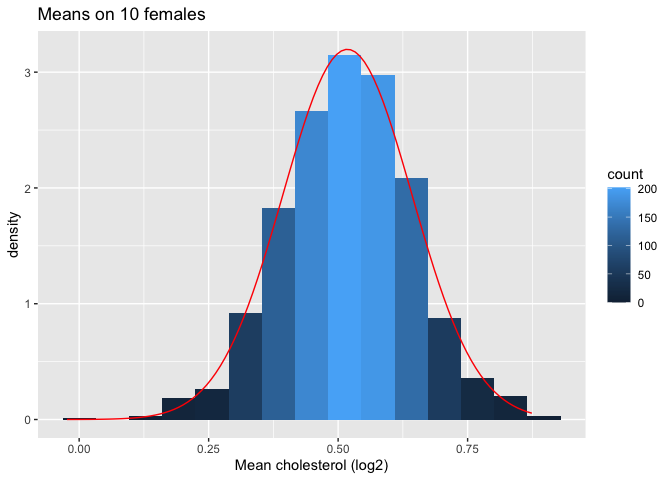
Vervolgens kijken we naar de verdeling van het steekproefgemiddelde over 1000 steekproeven van steekproefgrootte 10.

femSamp10 %>%
  log2 %>%
  colMeans %>%
  as.data.frame %>%
  ggplot(aes(x=.)) +
  geom_histogram(aes(y=..density.., fill=..count..),bins=15) +
  xlab("Mean cholesterol (log2)") +
  stat_function(
    fun=dnorm,
    color="red",
    args=list(
      mean=femSamp10%>%log2%>% colMeans %>% mean,
      sd=femSamp10%>%log2%>% colMeans %>% sd)
    ) +
  ggtitle("Means on 10 females")

femSamp10 %>%
  log2%>%
  colMeans %>%
  as.data.frame %>%  
  ggplot(aes(sample=.)) +
  stat_qq() +
  stat_qq_line() +
  ggtitle("Means on 10 females")

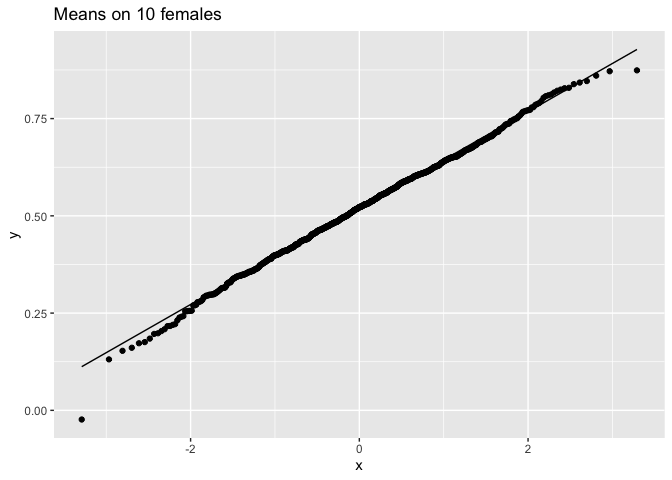
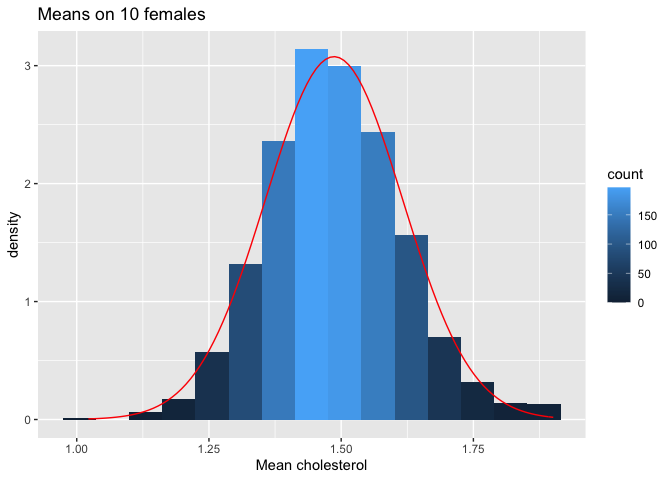
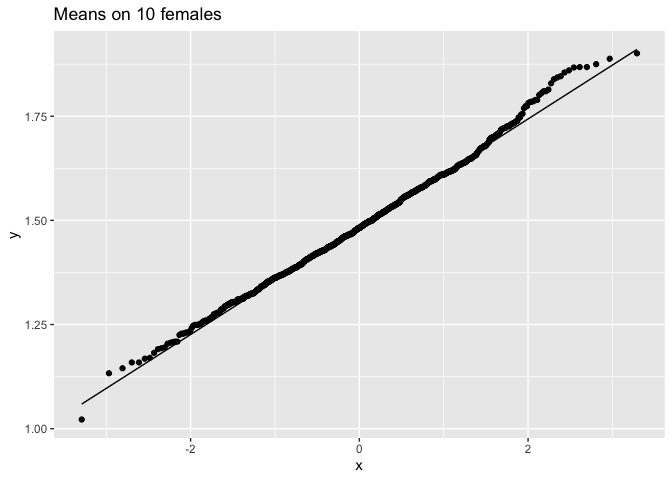
We hebben dus bevestigd dat het gemiddelde ongeveer normaal verdeeld is voor studies met 10 vrouwen, terwijl de originele gegevens ongeveer normaal verdeeld zijn.

Captopril studie

In het captopril voorbeeld zagen we dat de systolische bloeddrukverandering approximatief normaal verdeeld is. De standard error op de bloeddrukverandering bedroeg 2.32 mm Hg. Dus op 100 studies met n = 15 subjecten, verwachten we dat de geschatte gemiddelde systolische bloeddrukafwijking (\(\bar X\)) op minder dan 2 × 2.32 = 4.64mm Hg van het werkelijke populatiegemiddelde (\(\mu\)) ligt in 95 studies.

Niet-normaal verdeelde data

Als individuele observaties geen normale verdeling hebben, is \(\bar X\) nog steeds normaal verdeeld wanneer het aantaal observaties groot genoeg is.

Hoe groot moet de steekproef zijn om de normale benadering te laten werken hangt af van de scheefheid van de distributie!

NHANES: cholesterol

We kunnen dit evalueren in de NHanes-studie als we de gegevens niet log2 transformeren.

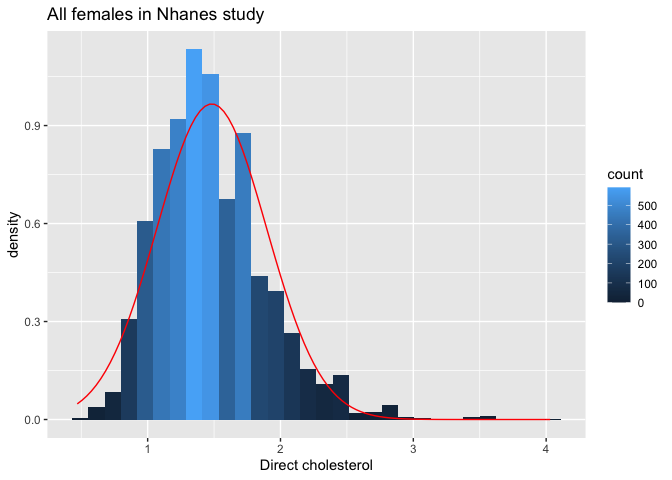
fem %>%
   ggplot(aes(x=DirectChol))+
   geom_histogram(aes(y=..density.., fill=..count..)) +
   xlab("Direct cholesterol") +
   stat_function(
     fun=dnorm,
     color="red",
     args=list(
       mean=mean(fem$DirectChol),
       sd=sd(fem$DirectChol))

    ) +
   ggtitle("All females in Nhanes study")

 fem %>%
  ggplot(aes(sample=DirectChol)) +
  stat_qq() +
  stat_qq_line() +
  ggtitle("All females in Nhanes study")

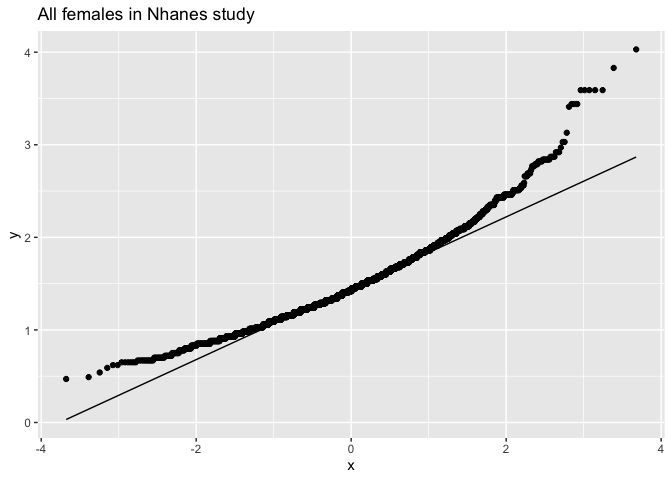
De cholesterol data zijn duidelijk niet-normaal verdeeld.

Verdeling van het steekproefgemiddelde voor verschillende steekproefgroottes

set.seed(121)
femSamp5 <- sapply(
  1:1000,
  function(j,x,size) sample(x,size),
  size = 5,
  x = fem$DirectChol)

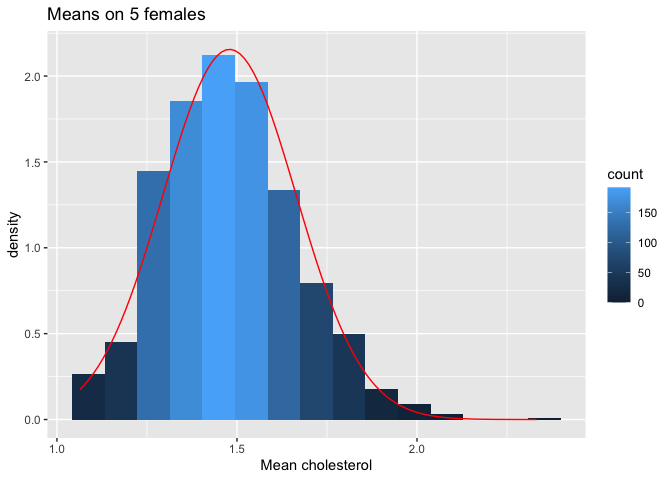
femSamp5 %>%
  colMeans %>%
  as.data.frame %>% ggplot(aes(x=.)) +
  geom_histogram(aes(y=..density.., fill=..count..),bins=15) +
  xlab("Mean cholesterol") +
  stat_function(
    fun=dnorm,
    color="red",
    args=list(
      mean=femSamp5%>% colMeans %>% mean,
      sd=femSamp5%>% colMeans %>% sd)
    ) +
  ggtitle("Means on 5 females")

femSamp5 %>%
  colMeans %>%
  as.data.frame %>%  
  ggplot(aes(sample=.)) +
  stat_qq() +
  stat_qq_line() +
  ggtitle("Means on 5 females")

femSamp10 %>%
  colMeans %>%
  as.data.frame %>% ggplot(aes(x=.)) +
  geom_histogram(aes(y=..density.., fill=..count..),bins=15) +
  xlab("Mean cholesterol") +
  stat_function(
    fun=dnorm,
    color="red",
    args=list(
      mean=femSamp10%>% colMeans %>% mean,
      sd=femSamp10%>% colMeans %>% sd)
    ) +
ggtitle("Means on 10 females")

femSamp10 %>%
  colMeans %>%
  as.data.frame %>%  
  ggplot(aes(sample=.)) +
  stat_qq() +
  stat_qq_line() +
  ggtitle("Means on 10 females")

femSamp50 %>%
  colMeans %>%
  as.data.frame %>%  
  ggplot(aes(sample=.)) +
  stat_qq() +
  stat_qq_line() +
  ggtitle("Means on 50 females")

femSamp100 %>%
  colMeans %>%
  as.data.frame %>%  
  ggplot(aes(sample=.)) +
  stat_qq() +
  stat_qq_line() +
  ggtitle("Means on 100 females")

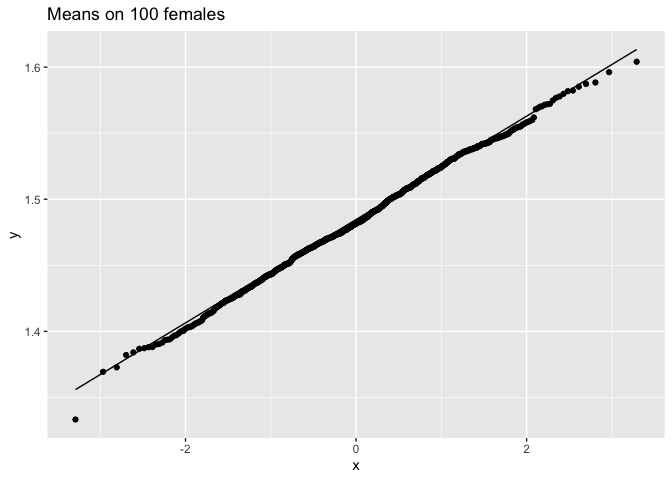
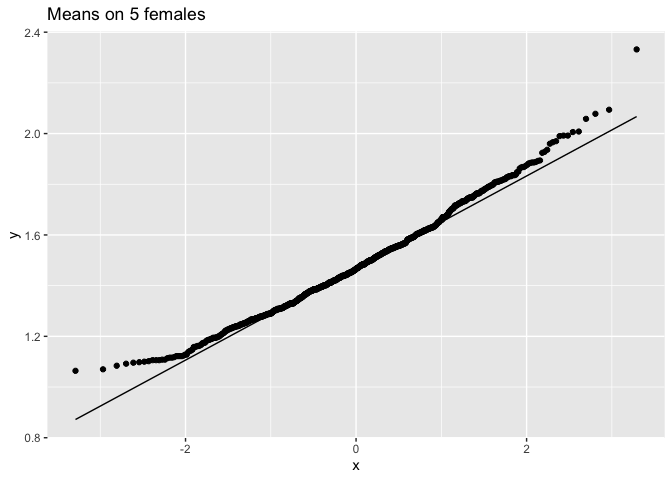
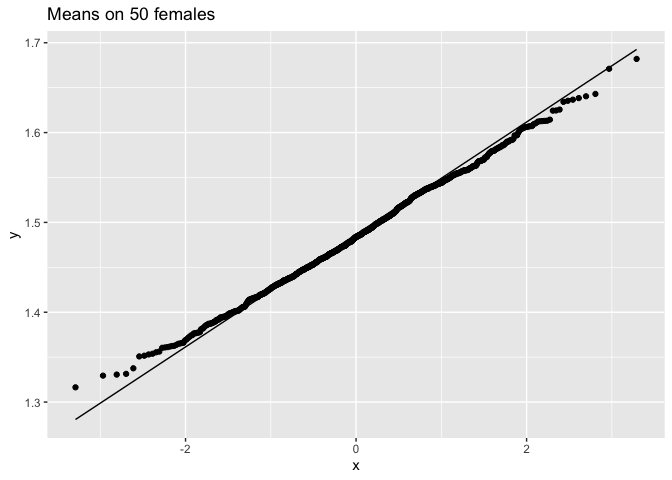
We merken op dat wanneer de data niet normaal verdeeld zijn, de verdeling van het steekproefgemiddelde niet normaal verdeeld is over kleine steekproeven

Voor grote steekproeven is het steekproefgemiddelde van niet-normale gegevens echter nog steeds ongeveer normaal verdeeld.

Centrale Limietstelling (CLT)

Stel dat \(X_1, X_2, \dots, X_n, \; n\) onafhankelijke lukrake trekkingen van de toevalsveranderlijke \(X\) voorstellen, met allen dezelfde theoretische verdeling. Laat \(X\) gemiddelde \(\mu\) en variantie \(\sigma^2\) hebben maar verder een ongespecifieerde verdeling, dan wordt de verdeling van het steekproefgemiddelde \(\bar{X}_n = {\sum_{i=1}^{n} X_i}/{n}\) naarmate \(n\) groter wordt steeds beter benaderd door de Normale verdeling met gemiddelde \(\mu\) en variantie \(\sigma^2/n.\)

Einde Stelling

Deze belangrijke eigenschap zal ons toelaten om de meeste technieken die in deze cursus aan bod komen toe te passen op een zeer uitgebreid spectrum van experimenten.