In het begin van onze jaartelling vestigden de Maya zich in Centraal-Amerika. Ze waren in vele opzichten veruit de meest ontwikkelde en fascinerende beschaving van hun tijd. Wielen en trekdieren waren hen dan wel onbekend, toch beheersten ze als geen ander de kunst van het weven, de architectuur en het pottenbakken. Maar echt adembenemend waren hun verwezenlijkingen op het vlak van wiskunde en sterrenkunde. Terwijl Europa zich door de donkere Middeleeuwen aan het slepen was, berekenden de Maya het zonnejaar op 365,242 dagen (volgens moderne berekeningen 365,242198 dagen) en de maancyclus op 29,5302 dagen (volgens moderne berekening 29,53059 dagen). Zo'n verbluffend accurate berekeningen waren nauwelijks mogelijk geweest zonder het krachtige talstelsel dat de Maya hanteerden.
Mayapriesters en sterrenkundigen gebruikten een talstelsel met basis 20. Daarin worden de cijfers (0-19) voorgesteld aan de hand van drie symbolen: nul (vorm van een schelp), één (een punt) en vijf (een horizontale streep). Zo wordt negentien (19) bijvoorbeeld geschreven als vier punten horizontaal achter elkaar, boven drie horizontale strepen die bovenop elkaar gestapeld worden. De concepten 'cijfer' en 'nul' waren vrij ongebruikelijk voor die tijd, en nog totaal onbekend in Europa.
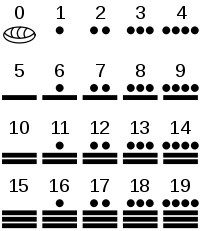
Voor mayagetallen bestaande uit meerdere mayacijfers — dus getallen met waarde groter dan 19 — worden de mayacijfers verticaal bovenop elkaar geschreven. Hierbij staat het cijfer met de hoogste getalwaarde bovenaan. Het getal drieëndertig wordt bijvoorbeeld geschreven als een punt (bovenste mayacijfer), met daaronder drie punten bovenop 2 horizontale strepen (onderste mayacijfer). Het eerste punt stelt dus "één twintig" of $$1 \times 20$$ voor, waarbij drie punten en twee horizontale strepen (dus 13) opgeteld worden. Bijgevolg krijg je $$(1 \times 20) + 13 = 33$$. Vreemd genoeg heeft in het Maya-talstelsel het cijfer op de derde positie (geteld vanaf onder) niet als getalwaarde $$20 \times 20 = 400$$, maar $$18 \times 20 = 360$$. Vermoedelijk omdat 360 ongeveer gelijk is aan het aantal dagen in een kalenderjaar. Alle mayacijfers boven de derde positie (geteld vanaf onder) hebben terug een normale getalwaarde volgens het 20-tallig stelsel, dus voor het vierde cijfer $$360 \times 20 = 7200$$, voor het vijfde cijfer $$7200 \times 20 = 144000$$, enzoverder. Op die manier geeft onderstaande tabel bijvoorbeeld aan dat $$12 \times 360 + 16 \times 20 + 5 = 4645$$ en dat $$9 \times 7200 + 5 \times 360 + 13 \times 20 + 16 = 66876$$.
| eenheid | 33 | 389 | 4645 | 66876 |
|---|---|---|---|---|
| 7200 |
|
|||
| 360 |
|
|
|
|
| 20 |
|
|
|
|
| 1 |
|
|
|
|
Opgave
Bij deze opgave stellen we mayagetallen en mayacijfers voor als strings. Het mayacijfer met waarde nul wordt genoteerd met de letter S, en de andere cijfers als een reeks punten (.; waarde 1) en koppeltekens (-; waarde 5), waarbij de punten altijd voor de koppeltekens staan. De mayacijfers van een mayagetal worden van links naar rechts achter elkaar geschreven — gescheiden door een spatie — in plaats van van boven naar onder. Op die manier wordt het mayagetal met getalwaarde 66876 dus voorgesteld als de string "....- - ...-- .---". Gevraagd wordt om een functie maya2deci te schrijven die de decimale waarde teruggeeft voor een gegeven mayagetal. De stringvoorstelling van dit mayagetal moet als argument aan de functie doorgegeven worden.
Voorbeeld
>>> maya2deci('..')
2
>>> maya2deci('. ...--')
33
>>> maya2deci('. . ....-')
389
>>> maya2deci('..-- .--- -')
4645
>>> maya2deci('. ..--- ...- ---')
13495
>>> maya2deci('....- - ...-- .---')
66876
>>> maya2deci('...- .-- S S S')
1231200