De elementen in dit vierkant rooster bestaan uit de eerste 25 natuurlijke getallen. Kies vijf elementen — waarbij er nooit twee elementen in dezelfde rij of in dezelfde kolom staan — zodat het grootste element zo klein mogelijk is.

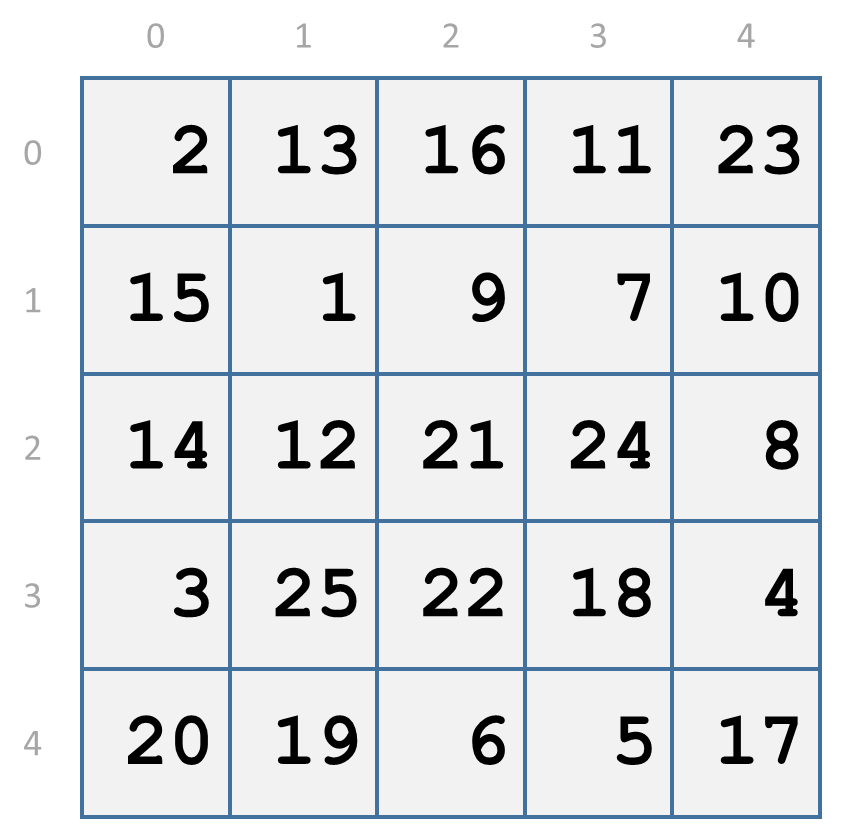
Sidney Penner van het Bronx Community College (CUNY, Bronx, New York) vond de oplossing door eerst alle elementen groter dan 11 te schrappen. Daardoor worden in rij 2 alle elementen geschrapt, behalve het element 8. Als we element 8 selecteren, dan worden alle andere elementen in rij 2 en in kolom 4 geschrapt. Hierbij nummeren we de rijen van boven naar onder en de kolommen van links naar rechts, telkens vanaf nul.

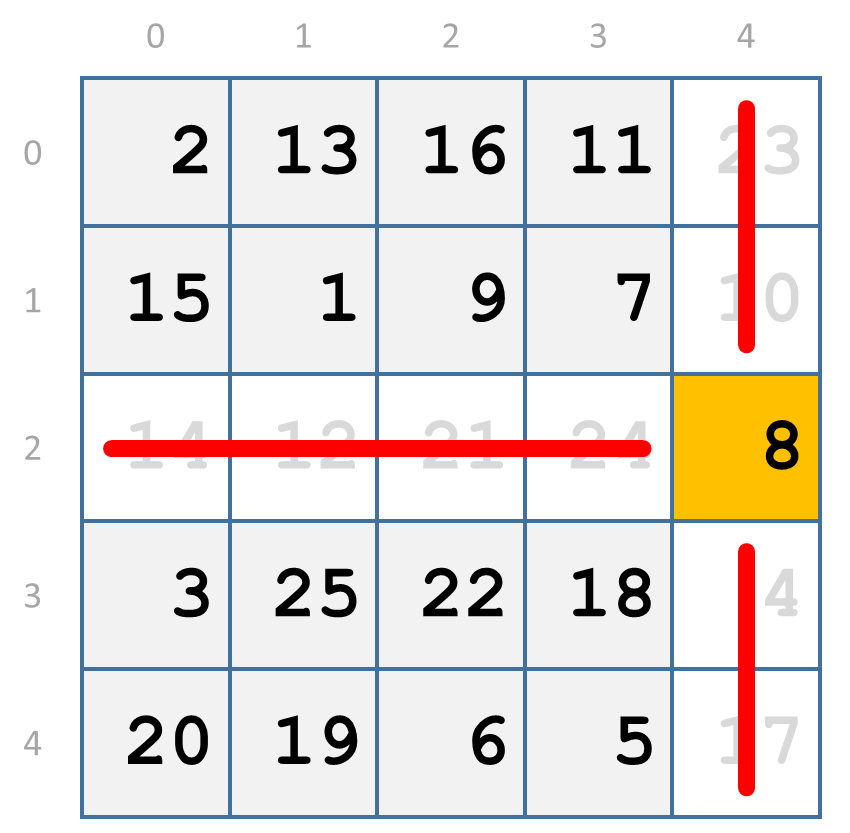
De geselecteerde elementen hebben we gemarkeerd met een gele achtergrondkleur en de elementen die nog kunnen geselecteerd worden met een grijze achtergrondkleur. De elementen die niet meer kunnen geselecteerd worden hebben we geschrapt met een dikke rode lijn en hebben we gemarkeerd met een witte achtergrondkleur. Rij 3 bevat nu nog maar één element dat kan geselecteerd worden en dat niet groter is dan 11. Als we element 3 selecteren, dan worden alle andere elementen in rij 3 en in kolom 0 geschrapt.

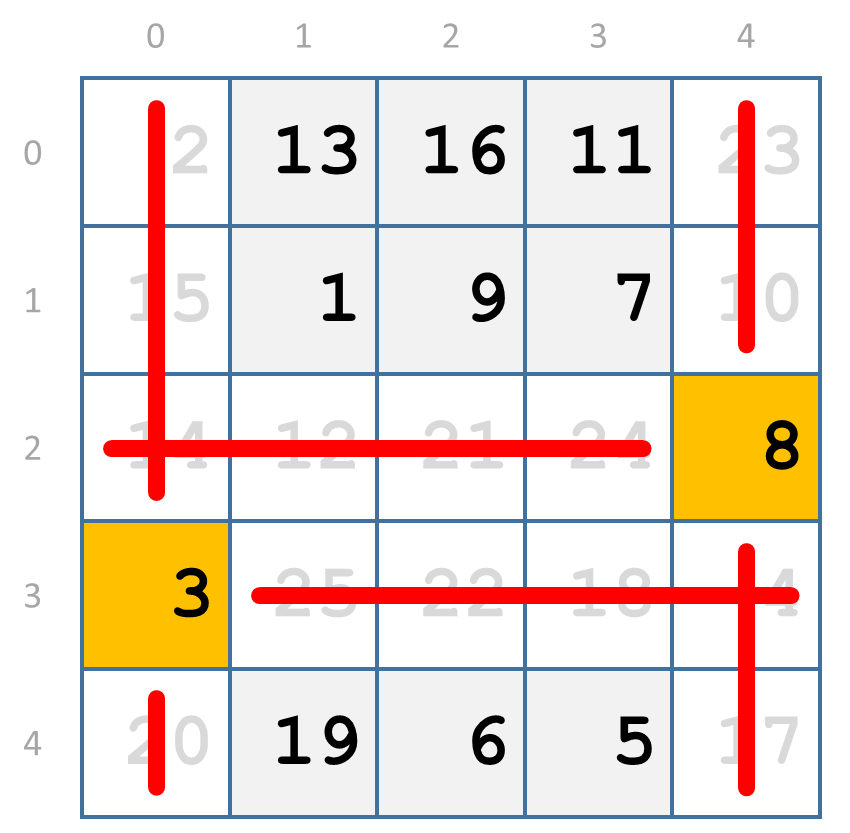
Als we op deze manier verdergaan dan selecteren we uiteindelijk de elementen 1, 3, 6, 8 en 11.

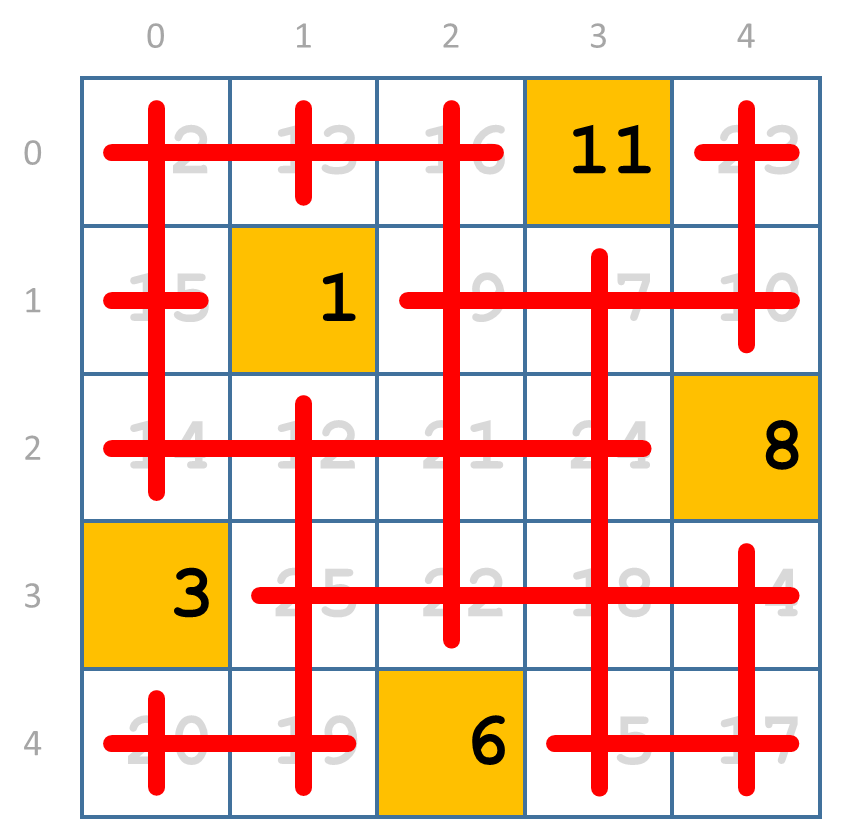
Er kunnen geen vijf elementen gevonden worden die allemaal op verschillende rijen en kolommen staan, en waarvan de grootste waarde kleiner is dan 11.

Opgave

Definieer een klasse Rooster waarmee vierkante roosters kunnen voorgesteld worden waarvan de elementen gehele getallen zijn. De elementen moeten allemaal verschillend zijn, en er moeten elementen kunnen geselecteerd worden die allemaal op een verschillende rij en een verschillende kolom van het rooster staan. De rijen van een rooster worden van boven naar onder genummerd en de kolommen van links naar rechts, telkens vanaf nul.

Bij het instantiëren van objecten van de klasse Rooster moet als argument een lijst (list) van verschillende gehele getallen (int) doorgegeven worden. De elementen van het rooster worden van links naar rechts, en van boven naar onder gevuld met de getallen uit de gegeven lijst. Daardoor moet het aantal getallen in de lijst een kwadraatgetal¹ zijn. Indien het argument dat wordt doorgegeven bij het instantiëren van een object van de klasse Rooster niet voldoet aan de gestelde voorwaarden, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige elementen. Voorts moet de klasse Rooster minstens de volgende methoden ondersteunen:

• Een methode element waaraan een rij- en een kolomindex moeten doorgeven worden. De methode moet het getal teruggeven uit de cel van het rooster op de gegeven rij en de gegeven kolom.

• Een methode positie waaraan een geheel getal (int) moet doorgegeven worden. De methode moet een tuple teruggeven met de rij- en kolomindex van de cel in het rooster die het gegeven getal bevat.

• Een methode selecteer waaraan een geheel getal (int) moet doorgegeven worden. De methode moet ervoor zorgen dat het gegeven getal geselecteerd wordt. Dit betekent dat na die selectie geen enkel ander getal op dezelfde rij en dezelfde kolom nog kan geselecteerd worden (inclusief het getal dat aan de methode wordt doorgegeven). De methode moet een referentie teruggeven naar het object waarop de methode werd aangeroepen. Indien het gegeven getal zelf niet meer kan geselecteerd worden, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige selectie.

• Een methode is_geschrapt waaraan een rij- en een kolomindex moeten doorgeven worden. De methode moet een Booleaanse waarde teruggeven, die aangeeft of het getal op de gegeven positie in het rooster reeds geschrapt werd door het selecteren van andere getallen. Merk op dat getallen die geselecteerd worden zelf niet geschrapt worden. Enkel de getallen op dezelfde rij en dezelfde kolom als het geselecteerde getal worden geschrapt.

Als de rij- en kolomindex die aan de methoden getal of is_geschrapt doorgeven worden geen geldige positie van een cel in het rooster aanduiden, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige positie.

Als het getal dat aan de methoden positie of selecteer doorgegeven wordt niet in het rooster voorkomt, dan moet een AssertionError opgeworpen worden met de boodschap element niet gevonden.

Zorg ervoor dat de ingebouwde functie str een stringvoorstelling teruggeeft van de objecten van de klasse Rooster, waarbij alle rijen van het rooster op een afzonderlijke regel staan. De kolommen van het rooster moeten een vaste breedte hebben die gelijk is aan de maximale breedte van de stringvoorstelling van alle getallen in het rooster, en de getallen moeten rechts uitgelijnd worden in de kolommen. Tussen twee kolommen moet er telkens één spatie staan. Geschrapte elementen (zoals gedefinieerd door de methode is_geschrapt) moeten voorgesteld worden door een koppelteken (-).

Voorbeeld

>>> rooster = Rooster([2, 13, 16, 11, 23, 15, 1, 9, 7, 10, 14, 12, 21, 24, 8, 3, 25, 22, 18, 4, 20, 19, 6, 5, 17])
>>> print(rooster)
 2 13 16 11 23
15  1  9  7 10
14 12 21 24  8
 3 25 22 18  4
20 19  6  5 17
>>> rooster.element(2, 3)
24
>>> rooster.element(4, 1)
19
>>> rooster.element(5, -2)
Traceback (most recent call last):
AssertionError: ongeldige positie
>>> rooster.positie(24)
(2, 3)
>>> rooster.positie(19)
(4, 1)
>>> rooster.positie(42)
Traceback (most recent call last):
AssertionError: element niet gevonden
>>> print(rooster.selecteer(1))
 2  - 16 11 23
 -  1  -  -  -
14  - 21 24  8
 3  - 22 18  4
20  -  6  5 17
>>> rooster.is_geschrapt(1, 1)
False
>>> rooster.is_geschrapt(2, 4)
False
>>> rooster.is_geschrapt(3, 1)
True
>>> rooster.selecteer(1)
Traceback (most recent call last):
AssertionError: ongeldige selectie
>>> print(rooster.selecteer(3).selecteer(6))
 -  -  - 11 23
 -  1  -  -  -
 -  -  - 24  8
 3  -  -  -  -
 -  -  6  -  -
>>> rooster.selecteer(2)
Traceback (most recent call last):
AssertionError: ongeldige selectie
>>> print(rooster.selecteer(8).selecteer(11))
 -  -  - 11  -
 -  1  -  -  -
 -  -  -  -  8
 3  -  -  -  -
 -  -  6  -  -

>>> rooster = Rooster([2, 13, 16, 11, 23])
Traceback (most recent call last):
AssertionError: ongeldige elementen
>>> rooster = Rooster([1, 2, 2, 1])
Traceback (most recent call last):
AssertionError: ongeldige elementen

5 T=0
10 MAT READ M(5,5)
20 DATA 2, 13, 16, 11, 23
30 DATA 15, 1, 9, 7, 10
40 DATA 14, 12, 21, 24, 8
50 DATA 3, 25, 22, 18, 4
60 DATA 20, 19, 6, 5, 17
70 FOR H=1 TO 5
80 A(1)=M(1,H)
90 FOR I=1 TO 5
100 IF I=H THEN 260
110 A(2) = M(2,I)
120 FOR J=1 TO 5
130 IF J=H OR J=I THEN 250
140 A(3)=M(3,J)
150 FOR K=1 TO 5
160 IF K=H OR K=I OR K=J THEN 240
170 A(4) = M(4,K)
180 FOR L = 1 TO 5
190 IF L=H OR L=I OR L=J OR L=K THEN 230
200 A(5) = M(5,L)
210 IF T=0 GO TO 500
220 GO SUB 600
230 NEXT L
240 NEXT K
250 NEXT J
260 NEXT I
270 NEXT H 
280 PRINT "THE REQUIRED ELEMENTS ARE IN THE LINE ABOVE."
290 END
500 B=A(1)
510 FOR C=2 TO 5
520 IF B>A(C) THEN 540
530 B=A(C)
540 NEXT C
560 T=1
570 GO TO 230
600 D=A(1)
610 FOR E=2 TO 5
620 IF B>A(E) THEN 640
630 D=A(E)
640 NEXT E
650 IF D>=B GO TO 680
660 PRINT D,M(1,H);M(2,I);M(3,J);M(4,K);M(5,L)
670 B=D
680 RETURN

READY

RUN
 18    2   1   8   18   6
 12    2   9   12   4   5
 11    11   1   8   3   6
THE REQUIRED ELEMENTS ARE IN THE LINE ABOVE

READY

Bronnen

• Bankoff L (1976). Problem department: puzzle 377 proposed by Charles W. Trigg, San Diego, California. Pi Mu Epsilon Journal 6(5), 306–324. ⁴

• Bankoff L (1977). Problem department: puzzle 377 solution by Sidney Penner, Bronx Community College of CUNY, Bronx, New York. Pi Mu Epsilon Journal 6(7), 417–437. ⁵

• Bankoff L (1977). Problem department: puzzle 377 computer solution by Jeanette Bickley, Webster Groves Senior High School, Webster Groves, Missouri. Pi Mu Epsilon Journal 6(7), 417–437. ⁶