STEP 5: Dimensionality reduction
In the fifth step, we will use singular value decomposition as dimensionality reduction
technique. Before we can use SVD, we have to transform the data to a matrix.
Let’s start from the dtm_reviews_dense variable.
reviews_mat <- as.matrix(dtm_reviews_dense)
dim(reviews_mat)
[1] 5 169
Center the data when the features have very different scalings. We do not want to take scaling into account when considering the uniqueness of our features, luckily for us R does this by default.
s <- svd(reviews_mat)
str(s)
List of 3
$ d: num [1:5] 0.588 0.581 0.347 0.336 0.24
$ u: num [1:5, 1:5] -0.00141 -0.99963 -0.02096 -0.00556 -0.01627 ...
$ v: num [1:169, 1:5] -0.000154 -0.000154 -0.000154 -0.000154 -0.000154 ...
u is the document-by-concept matrix. This is the matrix we are interested in.
dim(s$u)
[1] 5 5
ncol(s$u) will be equal to ncol(reviews_mat) if nrow(reviews_mat) >= ncol(reviews_mat). Otherwise, ncol(s$u) will be equal to nrow(reviews_mat).
d represents the strength of each concept.
length(s$d)
[1] 5
v is the term-to-concept matrix, it shows how the terms are related to the concepts.
dim(s$v)
[1] 169 5
We will use u in our basetable.
head(s$u)
[,1] [,2] [,3] [,4] [,5]
[1,] -0.001407065 0.005107153 -0.23760912 -0.9703323103 -0.04437400
[2,] -0.999631566 -0.016867361 0.02059622 -0.0035011445 -0.00397022
[3,] -0.020958293 0.025005298 -0.96812152 0.2401274444 -0.06336417
[4,] -0.005558518 0.012982737 -0.07172679 -0.0279500349 0.99693260
[5,] -0.016266712 0.999447644 0.02671504 -0.0007454217 -0.01120501
However, it is important to note that we will want to deploy our model on future data. We can do that as follows:
head(reviews_mat %*% s$v %*% solve(diag(s$d)))
Docs [,1] [,2] [,3] [,4] [,5]
1 -0.001407065 0.005107153 -0.23760912 -0.9703323103 -0.04437400
2 -0.999631566 -0.016867361 0.02059622 -0.0035011445 -0.00397022
3 -0.020958293 0.025005298 -0.96812152 0.2401274444 -0.06336417
4 -0.005558518 0.012982737 -0.07172679 -0.0279500349 0.99693260
5 -0.016266712 0.999447644 0.02671504 -0.0007454217 -0.01120501
The only thing we need to do is replace reviews_mat with the new dtm.
Note: solve returns the inverse of diag(s$d),
it is equivalent to 1/s$d.
d is proportional to the variance that is explained. To compute the variance we proceed as follows:
(s$d^2)/(nrow(reviews_mat) - 1)
Finally, we can plot the explained variance per singular vector in a scree plot. The explained variance is the percentage of the total variance that is explained by svd. You can also just plot the singular vectors in a scree plot. There is almost no difference between both plots.
plot(s$d^2/sum(s$d^2),
type="b",
ylab="% variance explained",
xlab="Singular vectors",
xaxt="n"
)
axis(1,at=1:length(s$d^2/sum(s$d^2)))
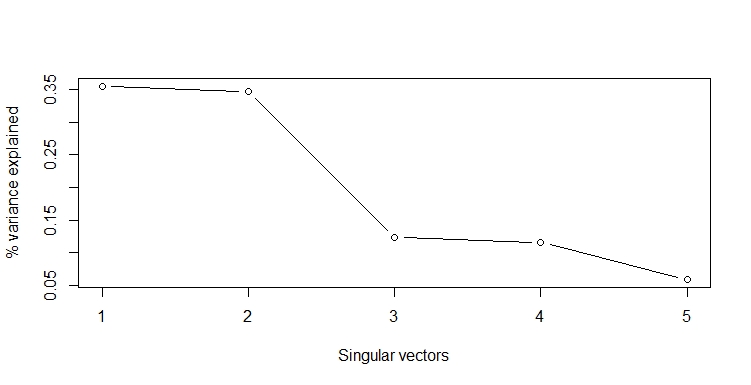
The first two singular vectors explain most of the variance. We could drop the last three without losing much information. However, when we look at the energy, we should retain 3 singular vectors
cumsum(s$d^2)/sum(s$d^2)
[1] 0.3552003 0.7020183 0.8254918 0.9410668 1.0000000
This shows that we can go from 171 columns (ncol(reviews_mat)) to 2, without
loosing much information. LSI means that we should only keep the first 2 columns of:
head(reviews_mat %*% s$v %*% solve(diag(s$d)))[,1:2].
Exercise 1
Transform product_reviews to a matrix and use the svd
function to create the variable s.
Exercise 2
Compute the strength of each concept and store it as d.
Check whether this matches your result that you obtained in exercise 1.
Exercise 3
Calculate the variance, using the formula above, and store it as variance.
To download the productreviews dataset click
here1.
Assume that:
- The tm package is loaded.