Een scherm bestaat uit 15 cellen die gerangschikt zijn in een rechthoekig $$5 \times 3$$ rooster met 5 rijen en 3 kolommen. Door de juiste cellen aan en uit te zetten, kunnen we op de volgende manier de tien cijfers van het scherm uitlezen.

Hierbij worden cellen die aan staan in het geel weergegeven, en cellen die uit staan in het donkergrijs. Merk op dat het cijfer 1 weergegeven wordt door de cellen in de middelste kolom aan te zetten, en niet de cellen in de linkse of rechtse kolom van het scherm. Dit is een detail dat wel degelijk belangrijk is met het oog op wat volgt.
Een uitlezing bestaat uit 15 cellen die gerangschikte zijn in een rechthoekig $$5 \times 3$$ rooster met 5 rijen en 3 kolommen. In dit geval bevat elke cel een natuurlijk getal dat voorgesteld wordt met cijfers die op een scherm weergegeven worden. Een uitlezing is dus een grote rechthoek die meerdere kleine rechthoeken (schermen) bevat, waarbij zowel de grote als de kleine rechthoeken dezelfde vorm hebben: $$5 \times 3$$ roosters met 5 rijen en 3 kolommen.
Voor elke uitlezing $$u$$ kunnen we een volgende uitlezing $$v$$ bepalen: het getal op positie X in uitlezing $$v$$ bepalen we door op alle schermen van uitlezing $$u$$ te tellen hoeveel cellen er aan staan op positie X. Als we dit toepassen op de twee uitlezingen hieronder dan zien we dat ze elkaar opvolgen, of anders gezegd, dat ze elkaar beschrijven. De cel linksboven in de rechtse uitlezing bevat bijvoorbeeld het getal 18. We kunnen nu makkelijk controleren dat van alle schermen in de linkse uitlezing, er precies 18 schermen zijn waarvan de cel linksboven aan staat. Neem bijvoorbeeld de cel linksboven in de linkse uitlezing. Die bevat twee schermen met cijfers 1 en 7 die samen het getal 17 vormen. De cel linksboven staat uit in het scherm met cijfer 1 en staat aan in het scherm met cijfer 7. Als we verdergaan naar de middelste cel op de bovenste rij van de linkse uitlezing, dan vinden we nog twee cellen die aan staan in de positie linksboven: één op het scherm met cijfer 2 en één op het scherm met cijfer 4. Tot nu toe staan er dus $$1 + 2 = 3$$ cellen aan in de positie linksboven. Als we de cellen van de linkse uitlezing in de gebruikelijke leesvolgorde aflopen, dan krijgen we de volgende reeks getallen met tussen ronde haakjes het aantal cellen die aan staan in de positie linksboven op de schermen met de cijfers van die getallen: 17(1), 24(2), 17(1), 13(1), 9(1), 15(1), 17(1), 25(2), 17(1), 8(1), 9(1), 14(1), 15(1), 24(2), 17(1). Het totaal aantal cellen linksboven die aan staan in alle schermen van de linkse uitlezing is dus 18, zoals we voorspeld hadden.

Als we starten met de linkse uitlezing en telkens de volgende uitlezing bepalen, dan bereiken we na twee stappen terug de linkse uitlezing. We zeggen dus dat de linkse uitlezing na twee stappen in herhaling valt. Een voor de hand liggende vraag is dan: zijn er ook zelfbeschrijvende uitlezingen. Dit zijn uitlezingen die reeds na één stap in herhaling vallen, of die met andere woorden zichzelf opvolgen. Zo'n uitlezingen bestaan inderdaad. Maar kan jij ze vinden?
Dit zijn de enige twee uitlezingen die zichzelf beschrijven. Je zal zien dat ze enkel verschillen in de meest linkse cel op de vierde rij. In de linkse uitlezing staat daar een scherm met cijfer 6. Als we in dat scherm de meest linkse cel op de vierde rij uitzetten, dan staat er op die positie nu één cel minder aan en verschijnt op het scherm effectief het cijfer 5.

Opgave
We lopen de cellen in het rooster van een scherm of een uitlezing altijd af in de gebruikelijke leesvolgorde: van links naar rechts en van boven naar onder. Deze volgorde wordt op het scherm hieronder aangegeven door de rode pijl. Op die manier nummeren we de opeenvolgende cellen vanaf nul, zoals aangeduid op de zwarte vakjes in de cellen van het scherm.
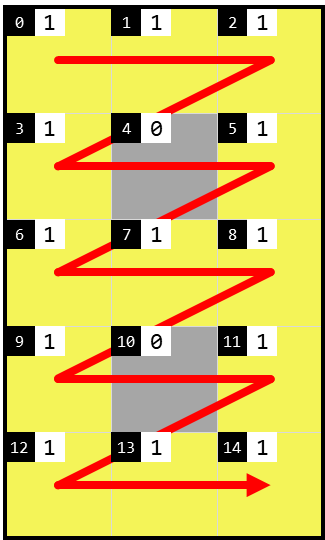
De bits van een scherm is een string (str) die bestaat uit 15 enen (1) en nullen (0). Hierbij lopen we de cellen in de gebruikelijke volgorde af, en stelt 1 een cel voor die aan staat en 0 een cel die uit staat. De witte vakjes in de cellen van bovenstaand scherm geven aan dat het cijfer 8 voorgesteld wordt op een scherm met bits 111101111101111. Dit zijn dan de bits van de schermen waarop de tien cijfers uitgelezen worden:
| cijfer | bits |
|---|---|
| 0 | 111101101101111 |
| 1 | 010010010010010 |
| 2 | 111001111100111 |
| 3 | 111001111001111 |
| 4 | 101101111001001 |
| 5 | 111100111001111 |
| 6 | 111100111101111 |
| 7 | 111001001001001 |
| 8 | 111101111101111 |
| 9 | 111101111001111 |
Scherm
Definieer een klasse Scherm waarmee schermen kunnen voorgesteld worden waarop één van de tien cijfers uitgelezen wordt. Bij het aanmaken van een scherm (Scherm) moet een cijfer (int) of bits (str) die corresponderen met een cijferscherm doorgegeven worden. Als er geen geldig argument wordt doorgegeven, dan moet een AssertionError opgeworpen worden met de boodschap ongeldig scherm.
Als er een scherm $$s$$ (Scherm) wordt doorgegeven aan de ingebouwde functie int, dan moet die het cijfer (int) op scherm $$s$$ teruggeven.
Als er een scherm $$s$$ (Scherm) wordt doorgegeven aan de ingebouwde functie repr, dan moet die een stringvoorstelling (str) teruggeven die leest als een Python expressie waarmee een nieuw scherm (Scherm) aangemaakt wordt dat hetzelfde cijfer weergeeft als op scherm $$s$$, waarbij dat cijfer als integer (int) doorgegeven wordt.
Als er een scherm $$s$$ (Scherm) wordt doorgegeven aan de ingebouwde functie str, dan moet die een stringvoorstelling (str) teruggeven die het cijfer op scherm $$s$$ weergeeft. Hierbij vormt elke rij van het rooster een afzonderlijke regel. Een cel die aan staat wordt voorgesteld door een hekje (#) en een cel die uit staat door een spatie.
Voorts moeten op een scherm $$s$$ (Scherm) minstens de volgende methoden kunnen aangeroepen worden:
-
Een methode bits waaraan geen argumenten moeten doorgegeven worden. De methode moet de bits van scherm $$s$$ teruggeven.
-
Een methode isopgelicht waaraan een getal $$n \in \mathbb{N}$$ (int) moet doorgegeven worden ($$0 \leq n < 15$$). De methode moet een Booleaanse waarde (bool) teruggeven, die aangeeft of de cel met volgnummer $$n$$ aan staat op scherm $$s$$.
Uitlezing
Definieer een klasse Uitlezing waarmee uitlezingen kunnen voorgesteld worden. Bij het aanmaken van een uitlezing (Uitlezing) moet een reeks (list of tuple) doorgegeven worden met de 15 natuurlijke getallen (int) in de opeenvolgende cellen van de uitlezing. Als er geen geldig argument wordt doorgegeven, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige uitlezing.
Als er een uitlezing $$u$$ (Uitlezing) wordt doorgegeven aan de ingebouwde functie list of tuple, dan moet die een lijst (list) resp. tuple (tuple) teruggeven met de 15 natuurlijke getallen (int) in de opeenvolgende cellen van uitlezing $$u$$.
Als er een uitlezing $$u$$ (Uitlezing) wordt doorgegeven aan de ingebouwde functie repr, dan moet die een stringvoorstelling (str) teruggeven die leest als een Python expressie waarmee een nieuwe uitlezing (Uitlezing) aangemaakt wordt met dezelfde getallen op corresponderende posities als bij uitlezing $$u$$, waarbij die getallen als tuple (tuple) doorgegeven worden.
Zorg ervoor dat de operator == kan gebruikt worden (u == v) om te controleren of twee uitlezingen $$u$$ en $$v$$ (Uitlezing) gelijk zijn. Dat is het geval als de getallen in overeenkomstige cellen van uitlezingen $$u$$ en $$v$$ gelijk zijn.
Voorts moeten op een uitlezing $$u$$ (Uitlezing) minstens de volgende methoden kunnen aangeroepen worden:
-
Een methode volgende waaraan geen argumenten moeten doorgegeven worden. De methode moet de uitlezing (Uitlezing) teruggeven die volgt op uitlezing $$u$$.
-
Een methode herhaling waaraan geen argumenten moeten doorgegeven worden. De methode moet teruggeven na hoeveel stappen (int) uitlezing $$u$$ in herhaling valt. Met andere woorden: als we telkens de volgende uitlezing blijven bepalen, na hoeveel stappen komen we dan bij een uitlezing die we eerder ook al waren tegengekomen (dat hoeft niet noodzakelijk de eerste uitlezing te zijn)?
Voorbeeld
>>> scherm = Scherm(8)
>>> int(scherm)
8
>>> scherm
Scherm(8)
>>> print(scherm)
###
# #
###
# #
###
>>> scherm.bits()
'111101111101111'
>>> scherm.isopgelicht(0)
True
>>> scherm.isopgelicht(4)
False
>>> scherm = Scherm('111101101101111')
>>> int(scherm)
0
>>> scherm
Scherm(0)
>>> print(scherm)
###
# #
# #
# #
###
>>> scherm.bits()
'111101101101111'
>>> scherm.isopgelicht(0)
True
>>> scherm.isopgelicht(4)
False
>>> Scherm(42)
Traceback (most recent call last):
AssertionError: ongeldig scherm
>>> Scherm('011111111111110')
Traceback (most recent call last):
AssertionError: ongeldig scherm
>>> uitlezing = Uitlezing([17, 24, 17, 13, 9, 15, 17, 25, 17, 8, 9, 14, 15, 24, 17])
>>> list(uitlezing)
[17, 24, 17, 13, 9, 15, 17, 25, 17, 8, 9, 14, 15, 24, 17]
>>> tuple(uitlezing)
(17, 24, 17, 13, 9, 15, 17, 25, 17, 8, 9, 14, 15, 24, 17)
>>> uitlezing
Uitlezing((17, 24, 17, 13, 9, 15, 17, 25, 17, 8, 9, 14, 15, 24, 17))
>>> uitlezing.volgende()
Uitlezing((18, 24, 18, 9, 9, 15, 13, 22, 18, 4, 9, 15, 10, 19, 18))
>>> uitlezing.volgende().volgende()
Uitlezing((17, 24, 17, 13, 9, 15, 17, 25, 17, 8, 9, 14, 15, 24, 17))
>>> uitlezing == uitlezing.volgende()
False
>>> uitlezing == uitlezing.volgende().volgende()
True
>>> uitlezing.herhaling()
2
>>> Uitlezing((18, 24, 18, 9, 9, 15, 13, 22, 18, 4, 9, 15, 10, 19, 18)).herhaling()
2
>>> Uitlezing((17, 24, 17, 9, 9, 15, 13, 20, 17, 6, 9, 14, 11, 20, 17)).herhaling()
1
>>> Uitlezing((17, 24, 17, 9, 9, 15, 13, 20, 17, 5, 9, 14, 11, 20, 17)).herhaling()
1
>>> Uitlezing([16, 2, 12, 18, 0, 8, 11, 16, 19, 29, 18, 13, 25, 7, 13]).herhaling()
64
>>> Uitlezing([7, 26, 27, 25, 11, 1, 7, 10, 12, 17, 11, 3, 10, 24, 30]).herhaling()
524
>>> Uitlezing((1, 2, 3))
Traceback (most recent call last):
AssertionError: ongeldige uitlezing