Een timmerman beschikt over drie houten balken van verschillende lengtes. Hij wil weten of hij hiermee een driehoekig frame in elkaar kan knutselen, zonder dat hij hierbij de balken moet verzagen.

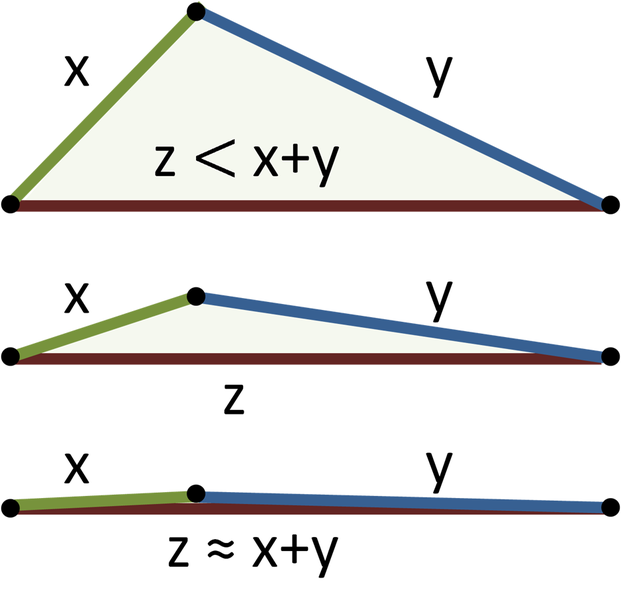
Dit zal enkel kunnen als de driehoeksongelijkheid geldt voor elk van deze drie balken. Deze ongelijkheid zegt dat voor drie zijden $$x$$, $$y$$ en $$z$$ in een driehoek moet gelden dat $$x + y > z$$. Anders gezegd komt dit erop neer dat een rechte altijd de kortste afstand is tussen twee punten.

Invoer

De lengtes van de drie houten balken, gegeven als reële getallen die elk op een afzonderlijke regel staan. Merk op dat de lengtes niet noodzakelijk gerangschikt zijn van klein naar groot.

Uitvoer

De vermelding "mogelijk" of "onmogelijk" naargelang het al dan niet mogelijk is om met de drie balken een driehoek te vormen.

Voorbeeld

Invoer:

1.5
1.5
3.0

Uitvoer:

onmogelijk

Voorbeeld

Invoer:

4.0
6.0
5.0

Uitvoer:

mogelijk