Generate a simulated two-class data set with 100 observations and two features in which there is a visible but non-linear separation between the two classes. Show that in this setting, a support vector machine with a polynomial kernel (with degree greater than 1) or a radial kernel will outperform a support vector classifier on the training data. Which technique performs best on test data? Make plots and report training and test error rates in order to back up your assertions.
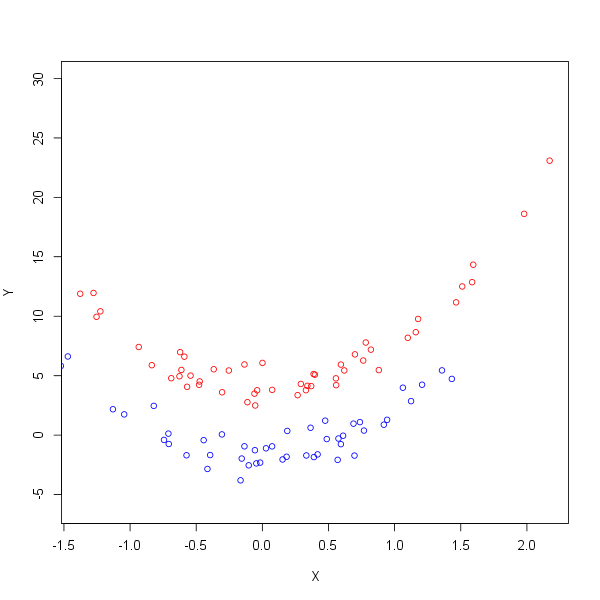
We begin by creating a data set with non-linear separation between the two classes.
set.seed(1)
x <- rnorm(100)
y <- 4 * x^2 + 1 + rnorm(100)
class <- sample(100, 50)
y[class] <- y[class] + 3
y[-class] <- y[-class] - 3
plot(x[class], y[class], col = "red", xlab = "X", ylab = "Y", ylim = c(-6, 30))
points(x[-class], y[-class], col = "blue")
z <- rep(-1, 100)
z[class] <- 1
data <- data.frame(x = x, y = y, z = as.factor(z))
\(x\) and \(y\) are your independent variables, \(z\) is the dependent variable.
All variables are stored in the dataframe data.
Questions
Show that in this setting, a support vector machine with a polynomial kernel (with degree greater than 1), or a radial kernel will outperform a support vector classifier on the training data.
-
Create a 50-50 train-test split. Set the seed to 5 and store the indices for the training samples in
train. -
Subset data into
data.trainanddata.testwith all training observations and test observations, respectively. -
Build a linear support vector machine with
cost = 10. Store the model insvm.linear. -
Calculate the accuracy of the model on the test data and store it in
acc.linear. -
Take a look at the plot
plot(svm.linear, data.train)and see how the linear model tries to separate a non-linear boundary. -
Repeat steps 3-5, but with a polynomial kernel with
degree = 2andcost = 10. Store the model and accuracy insvm.polyandacc.poly, respectively. -
Repeat steps 3-5, but with a radial kernel with
gamma = 1andcost = 10. Store the model and accuracy insvm.radialandacc.radial, respectively.
Assume that:
- The
e1071library has been loaded