Een kikker springt in onderstaand roosters telkens naar het vakje rechts, of naar het vakje eronder. Welke route geeft de kleinste som?

Geïnspireerd op een oefening uit Matrix 1.

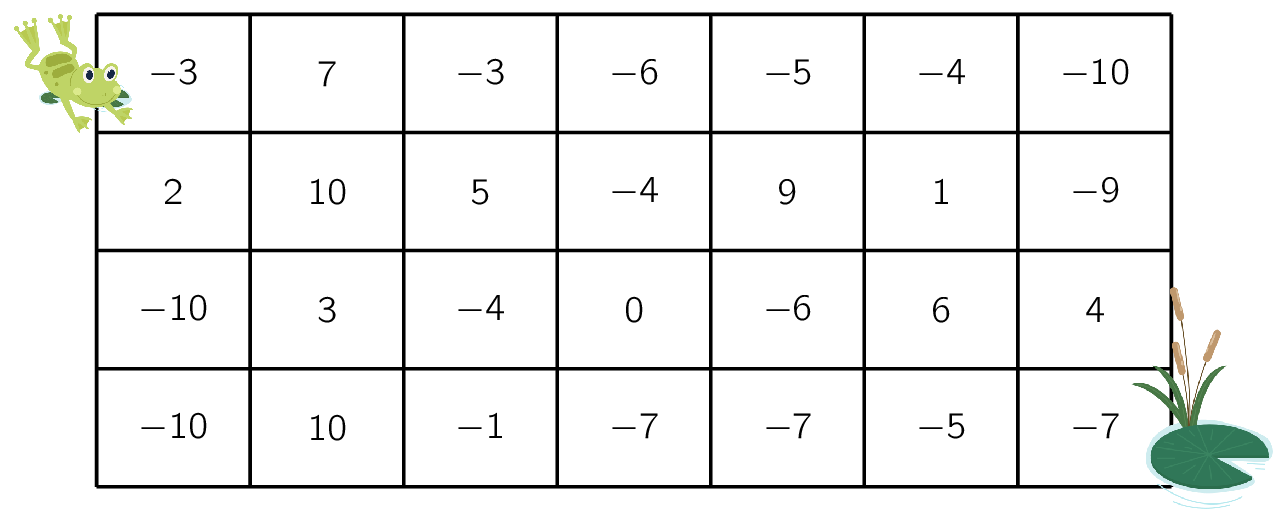
De kikker begint steeds op het vakje links boven en moet eindigen op het vakje rechts onderaan.

Gevraagd

Schrijf een functie kleinste_pad(tabel) die gegeven een matrix met gehele getallen de som bepaalt van het kleinste pad met behulp van een gretig algoritme. Indien je alle opties overloopt zal dit hoogst waarschijnlijk niet het kleinste pad zijn, maar slechts een benadering.

Voorbeeld

>>> kleinste_pad([[ -3,  7, -3, -6, -5, -4, -10], 
                  [  2, 10,  5, -4,  9,  1,  -9], 
                  [-10,  3, -4,  0, -6,  6,   4], 
                  [-10, 10, -1, -7, -7, -5,  -7]])
-38

Hierbij neemt de kikker de route volledig tot de onderste rij, waarna deze naar rechts beweegt.