Er heerst chaos in de luchtverkeerscentra van alle Europese luchthavens. De Eyjafjallajökull — een met ijs bedekte stratovulkaan in IJsland — is net tot uitbarsting gekomen. De aswolk die bij deze vulkaanuitbarsting is ontstaan, verspreidt zich razendsnel over het Europese vasteland. Een sluiting van het luchtruim boven een groot deel van Noord-Europa dient zich dan ook aan. Jouw taak bestaat erin om in kaart te brengen of er nog andere vulkanen tot uitbarsting komen en de verspreiding van de aswolken die daardoor ontstaan op de voet te volgen. Op basis van deze informatie moet je adviseren of er nog vluchten kunnen georganiseerd worden tussen twee gegeven luchthavens.

Om het overzicht te bewaren, hebben we een kaart opgedeeld in vierkante gebieden die samen een rechthoekig rooster vormen. Als een vulkaan tot uitbarsting komt, dan duiden we dit aan door het vierkant waarin de vulkaan gelegen is te markeren met een wolk. De verspreiding van aswolken wordt gemodelleerd, door bij elke volgende tijdsstap ook de vierkanten met een wolk te markeren die bovenaan, onderaan, links of rechts raken aan een vierkant dat reeds met een wolk gemarkeerd was. We hebben voor de eenvoud de kolommen in het onderstaande voorbeeldrooster oplopend genummerd van links naar rechts, en de rijen oplopend van onder naar boven. De volgorde van de nummering doet er voor deze opgave verder weinig toe, zolang ze maar gebeurt met oplopende gehele getallen. Op die manier kunnen we immers een bepaald vierkant van het rooster aanduiden met diens kolom- en rijnummer. Het voorbeeld toont hoe een aswolk zich na een vulkaanuitbarsting in het vierkant $$(0, 0)$$ gradueel verspreidt over aangrenzende vierkanten.

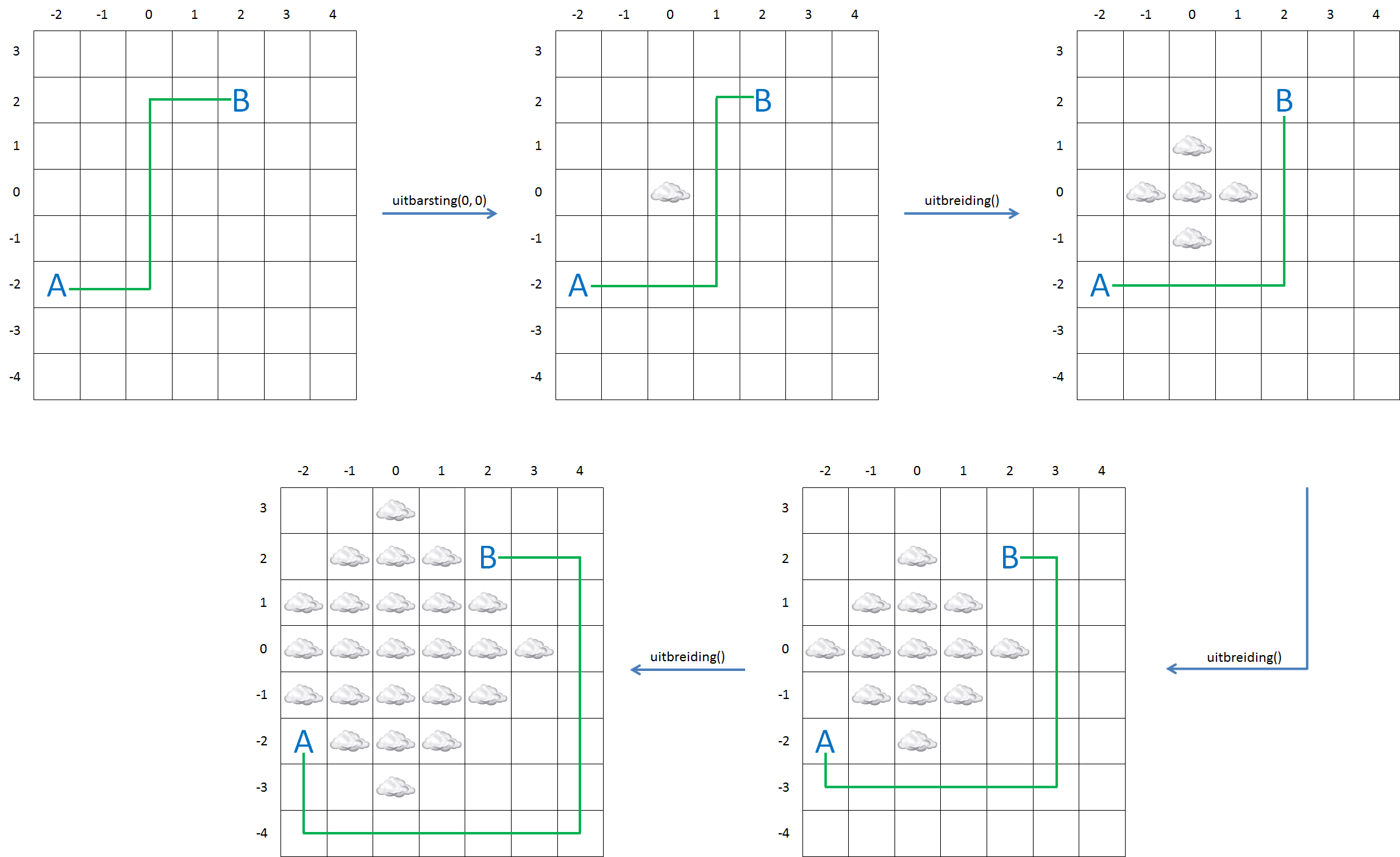
Om te adviseren of er nog vluchten kunnen georganiseerd worden tussen twee luchthavens, bepaal je de afstand van de kortste route die nog kan genomen worden om van de ene luchthaven naar de andere te vliegen zonder daarbij door een aswolk te vliegen. We zullen de procedure om deze afstand te bepalen, uitleggen aan de hand van onderstaande figuur. De vierkanten waarin de twee luchthavens gelegen zijn, worden aangeduid met de letters A en B. Een vliegroute kan geen vierkanten aandoen die met een wolk gemarkeerd zijn.

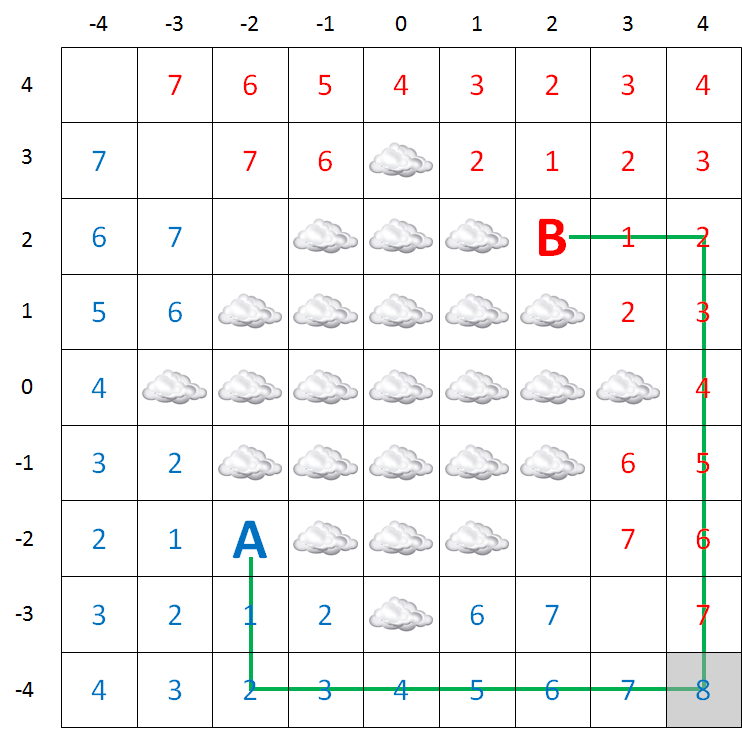
Als één van de luchthavens, of beide, zelf in een vierkant liggen die met een wolk gemarkeerd is, dan is het niet meer mogelijk om vanaf die luchthaven te vliegen. Anders kan de kortste route op de volgende manier bepaald worden:

markeer de vierkanten A en B met de waarde 0 (nul)
stel $$i$$ gelijk aan 0
markeer elk vierkant dat bovenaan, onderaan, links of rechts raakt aan een vierkant rondom A dat gemarkeerd is met de waarde $$i$$ en dat zelf nog niet gemarkeerd is (met een wolk of een getal) met de waarde $$i + 1$$; deze markeringen worden in bovenstaande afbeelding in het blauw weergegeven
markeer elk vierkant dat bovenaan, onderaan, links of rechts raakt aan een vierkant rondom B dat gemarkeerd is met de waarde $$i$$ en dat zelf nog niet gemarkeerd is (met een wolk of een getal) met de waarde $$i + 1$$; deze markeringen worden in bovenstaande afbeelding in het rood weergegeven
als er in stap 3 of in stap 4 geen bijkomende vierkanten konden genummerd worden, dan zijn de luchthavens volledig van elkaar afgesloten door de aswolk en kan er geen route gevonden worden
van zodra er tijdens stap 3 of 4 twee horizontaal of verticaal aangrenzende vierkanten zijn waarvan de ene met een blauw getal en de andere met een rood getal gemarkeerd is, dan heb je de kortste route gevonden en eindigt de procedure
verhoog $$i$$ met 1
spring terug naar stap 3

Het enige waarover je zelf nog even moet nadenken is hoe je de afstand van de kortste route bepaalt die je in stap 6 hebt gevonden. De afstand van een route wordt uitgedrukt als het aantal stappen naar naburige vierkanten (horizontaal of verticaal rakend aan het huidige vierkant) dat je moet nemen om van de ene luchthaven naar een andere luchthaven te gaan. In bovenstaand voorbeeld is de kortste route dus 16.

Opgave

Definieer een klasse Kaart waarmee de evolutie van aswolken boven een rechthoekig rooster kan opgevolgd worden, en waarmee de kortste route tussen twee luchthavens — die niet door een aswolk loopt — kan bepaald worden. De objecten van deze klasse moeten minstens over de volgende eigenschappen en methoden beschikken:

Elk object van de klasse Kaart moet gegarandeerd een eigenschap aswolk hebben, die verwijst naar een verzameling. Bij het aanmaken van een nieuw object is deze verzameling nog leeg, maar de volgende twee methoden worden gebruikt om de inhoud van de verzameling te wijzigen.
Een methode uitbarsting waaraan twee gehele getallen moeten doorgegeven worden. Deze getallen geven respectievelijk het kolomnummer $$k$$ en rijnummer $$r$$ aan van een vierkant in het rooster waarin zich een vulkaanuitbarsting voordoet. Het feit dat hierdoor boven dit vierkant gebied een aswolk ontstaat, wordt bijgehouden door het tuple $$(k, r)$$ toe te voegen aan de verzameling aswolk.
Een methode uitbreiding waaraan geen argumenten moeten doorgegeven worden. Door het aanroepen van deze methode worden de coördinaten van alle vierkanten aan de verzameling aswolk toegevoegd, die zelf links, rechts, bovenaan of onderaan raken aan een vierkant dat reeds met een aswolk gemarkeerd was.
Een methode kortsteRoute waaraan twee tuples met de coördinaten van twee luchthavens moeten doorgegeven worden. De methode moet de lengte van de kortste route tussen de twee luchthavens teruggegeven, die niet door een aswolk passeert. Indien één van beide luchthavens zelf onder een aswolk ligt, of indien de twee luchthavens volledig van elkaar zijn afgesloten, dan moet de waarde -1 als resultaat teruggegeven worden.

Voorbeeld

>>> kaart = Kaart()
>>> kaart.uitbarsting(0, 0)
>>> kaart.aswolk
{(0, 0)}
>>> kaart.uitbreiding()
>>> kaart.aswolk
{(0, 1), (0, -1), (1, 0), (0, 0), (-1, 0)}
>>> kaart.kortsteRoute((-2, -2), (2, 2))
8
>>> kaart.uitbreiding()
>>> kaart.aswolk
{(0, 1), (-1, 1), (0, 0), (-1, 0), (-1, -1), (1, 1), (2, 0), (0, -2), (0, -1), (1, 0), (1, -1), (0, 2), (-2, 0)}
>>> kaart.kortsteRoute((-2, -2), (2, 2))
12
>>> kaart.uitbreiding()
>>> kaart.kortsteRoute((-2, -2), (2, 2))
16
>>> kaart.uitbreiding()
>>> kaart.kortsteRoute((-2, -2), (2, 2))
-1