Teken een omgekeerde driehoek (punt naar beneden) van zeshoekige cellen.
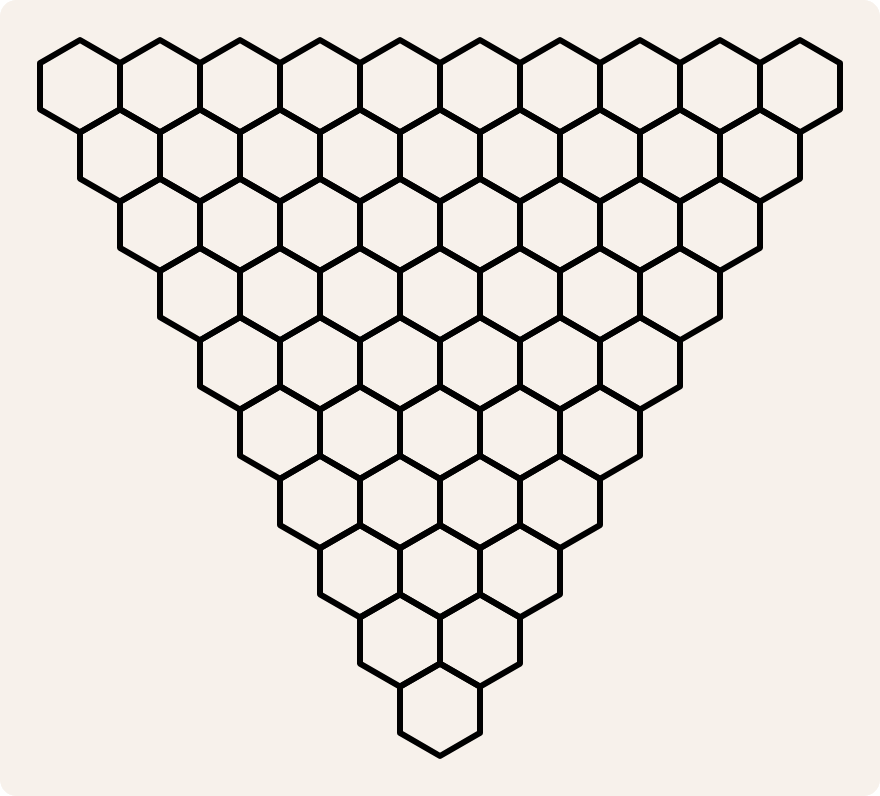
Kleur de cellen van de bovenste rij willekeurig in drie kleuren: rood, geel en blauw.
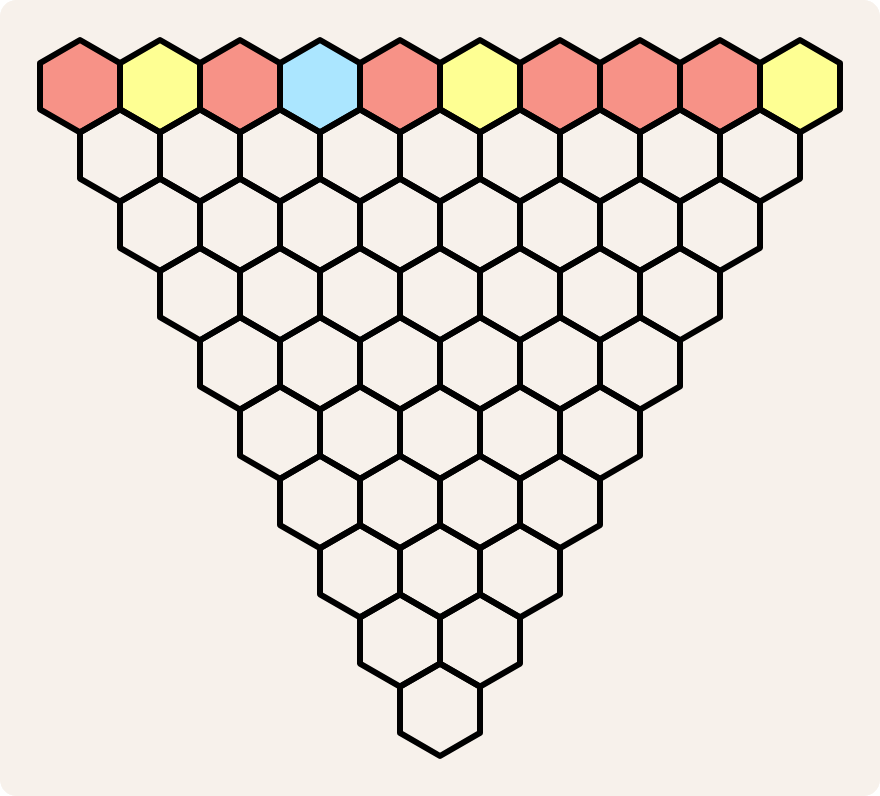
Kleur nu de cellen op de tweede rij volgens deze regels:
-
als de twee aangrenzende cellen direct erboven dezelfde kleur hebben, gebruik dan die kleur
-
als de twee aangrenzende cellen direct erboven een verschillende kleur hebben, gebruik dan de derde kleur
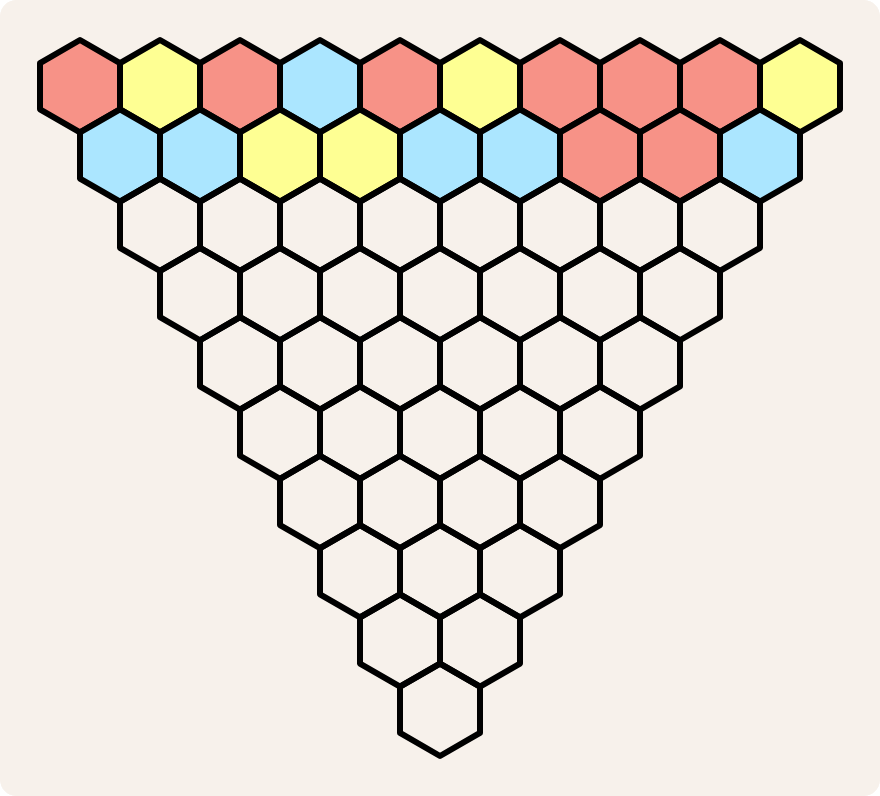
Als je klaar bent met de tweede rij, ga dan verder met de volgende rijen en pas dezelfde regels toe.
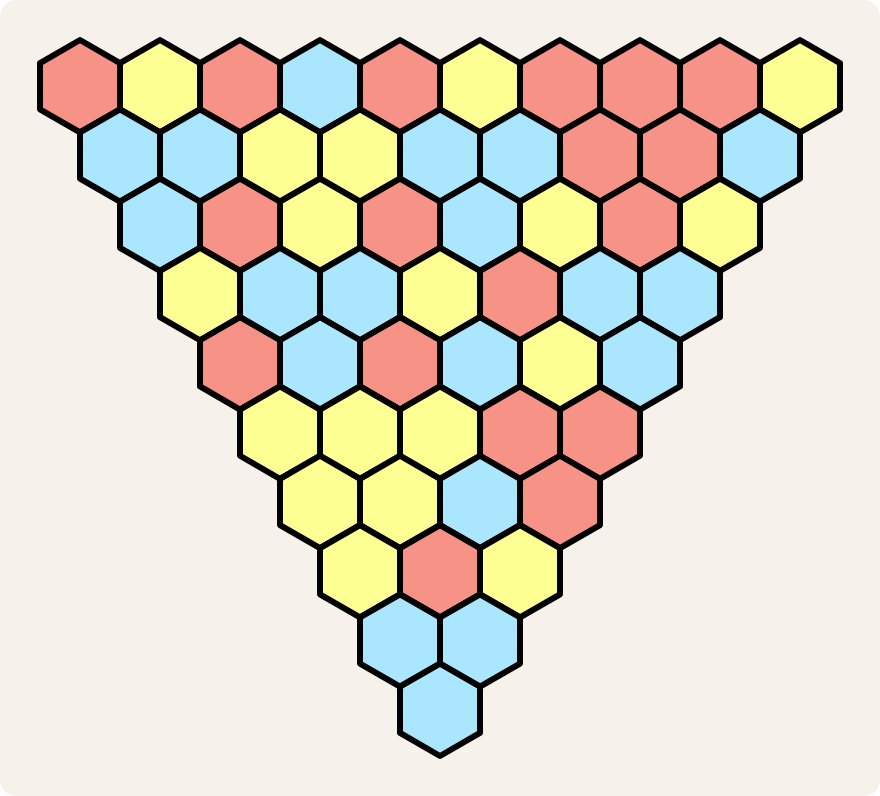
Als de bovenste rij van de driehoek bestaat uit $$3^n + 1$$ cellen (2, 4, 10, 28, …), dan is het mooie van deze procedure dat je meteen al de kleur van de onderste cel kan voorspellen: pas gewoon onze twee regels toe op de buitenste cellen van de bovenste rij. Als die twee cellen allebei rood zijn, dan zal de onderste cel ook rood zijn. Als één cel rood is en de andere geel (zoals in het voorbeeld hierboven), dan zal de onderste cel blauw zijn.
Opgave
Een gekleurde cel stellen we voor als het karakter (str) dat een vierkant in de corresponderende kleur voorstelt: '🟨' (geel), '🟥' (rood) of '🟦' (blauw).
Weergave van gekleurde vierkanten in PyCharm onder MS Windows
In PyCharm onder MS Windows zien de karakters voor gekleurde vierkanten eruit als monochrome vierkanten die per kleur een andere arcering hebben. Daardoor is het verschil tussen de drie karakters wat subtieler, maar voor de rest blijven het gewoon drie verschillende karakters.
Een rij gekleurde cellen stellen we voor als een string (str) met de voorstellingen van de gekleurde cellen, opgelijst van links naar rechts.
Een omgekeerde driehoek van gekleurde cellen stellen we voor als een lijst (list) van rijen gekleurde cellen (str), opgelijst van boven naar onder.
Gevraagd wordt:
-
Schrijf een functie kleur waaraan twee gekleurde cellen (str) moet doorgegeven worden die in een omgekeerde driehoek direct aangrenzen boven een derde gekleurde cel. De functie moet die derde gekleurde cel (str) teruggeven, waarbij de kleur bepaald wordt door onze twee regels toe te passen.
-
Schrijf een functie onderste_kleur waaraan een rij gekleurde cellen (str) moet doorgegeven worden. De functie moet de gekleurde cel (str) teruggeven die men bekomt door onze twee regels toe te passen op de buitenste cellen van de gegeven rij gekleurde cellen.
Opmerking
Anders dan de naam onderste_kleur misschien doet vermoeden, moet het resultaat van deze functie dus niet noodzakelijk een correcte voorspelling zijn voor de kleur van de onderste cel van een omgekeerde driehoek waarvan de cellen op de bovenste rij ingekleurd zijn volgens het patroon van de gegeven rij gekleurde cellen. Die voorspelling is enkel met zekerheid correct als de bovenste rij bestaat uit $$3^n + 1$$ cellen. Maar daar hoeft je implementatie van deze functie zich dus niets van aan te trekken.
-
Schrijf een functie volgende_rij waaraan een rij gekleurde cellen (str) moet doorgegeven worden. De functie moet de volgende rij gekleurde cellen (str) van een omgekeerde driehoek teruggeven, die men bekomt door onze twee regels toe te passen op de gegeven rij gekleurde cellen.
-
Schrijf een functie driekleurendriehoek waaraan een rij gekleurde cellen (str) moet doorgegeven worden. De functie moet de omgekeerde driehoek (list) van gekleurde cellen teruggeven, waarvan de cellen op de bovenste rij ingekleurd zijn volgens het patroon van de gegeven rij gekleurde cellen.
Voorbeeld
>>> kleur('🟥', '🟥')
'🟥'
>>> kleur('🟨', '🟥')
'🟦'
>>> onderste_kleur('🟥🟨🟥🟦🟥🟨🟥🟥🟥🟨')
'🟦'
>>> volgende_rij('🟥🟨🟥🟦🟥🟨🟥🟥🟥🟨')
'🟦🟦🟨🟨🟦🟦🟥🟥🟦'
>>> volgende_rij('🟦🟦🟨🟨🟦🟦🟥🟥🟦')
'🟦🟥🟨🟥🟦🟨🟥🟨'
>>> driekleurendriehoek('🟥🟨🟥🟦🟥🟨🟥🟥🟥🟨')
['🟥🟨🟥🟦🟥🟨🟥🟥🟥🟨', '🟦🟦🟨🟨🟦🟦🟥🟥🟦', '🟦🟥🟨🟥🟦🟨🟥🟨', '🟨🟦🟦🟨🟥🟦🟦', '🟥🟦🟥🟦🟨🟦', '🟨🟨🟨🟥🟥', '🟨🟨🟦🟥', '🟨🟥🟨', '🟦🟦', '🟦']
Epiloog
Dit principe werd in 2012 ontdekt door Steve Humbolt, die leerkrachten lager en secundair onderwijs opleidt aan de faculteit Onderwijs van de Newcastle University in het noordoosten van Engeland. Hij zei daarover:
Wat de ontdekking betreft: dat was precies wat het was — ik wilde het met gezinnen hebben over willekeurigheid en heb daarom dit kleurenspel bedacht. Het idee was om te laten zien hoe orde kan ontstaan uit wanorde. Net zoals in dit lappendeken van kleurvlakken.
Toen ik dit spel aan het uitwerken was, merkte ik dat de twee bovenste kleuren de onderste kleur opleverden. Ik schreef wat computercode en ontdekte dat niet alle gevallen werkten, maar ik kon geen volledig bewijs vinden. Ik beschreef het probleem in de zomer tijdens een conferentie in Murcia aan Ehrhard Behrends. Binnen een paar dagen kwam hij terug met een bewijs – en toen hebben we samen een artikel geschreven. Ehrhards genialiteit was om het probleem te veralgemenen naar $$n$$ kleuren en te kijken naar alle verschillende manieren waarop we de oorspronkelijke regels voor het creëren van het patroon konden opstellen.