Game of dots is een spel voor twee spelers dat met potlood en papier kan gespeeld worden. Het werd in de negentiende eeuw bedacht door de Franse wiskundige Édouard Lucas, die het la pipopipette noemde. Het spel wordt gespeeld op een rechthoekig raster van stippen, dat bij aanvang nog leeg is. Om de beurt trekken de spelers een lijn tussen twee aangrenzende stippen die nog niet met elkaar verbonden waren. Een speler die de vierde lijn van een $$1 \times 1$$-vakje aanvult, scoort één punt en blijft aan de beurt. Het spel eindigt als er geen lijnen meer kunnen getrokken worden. De winnaar is de speler die het meeste punten gescoord heeft.

Voorbeeld van het verloop van een spelletje game of dots dat gespeeld wordt op een vierkant raster van $$3 \times 3$$ stippen.

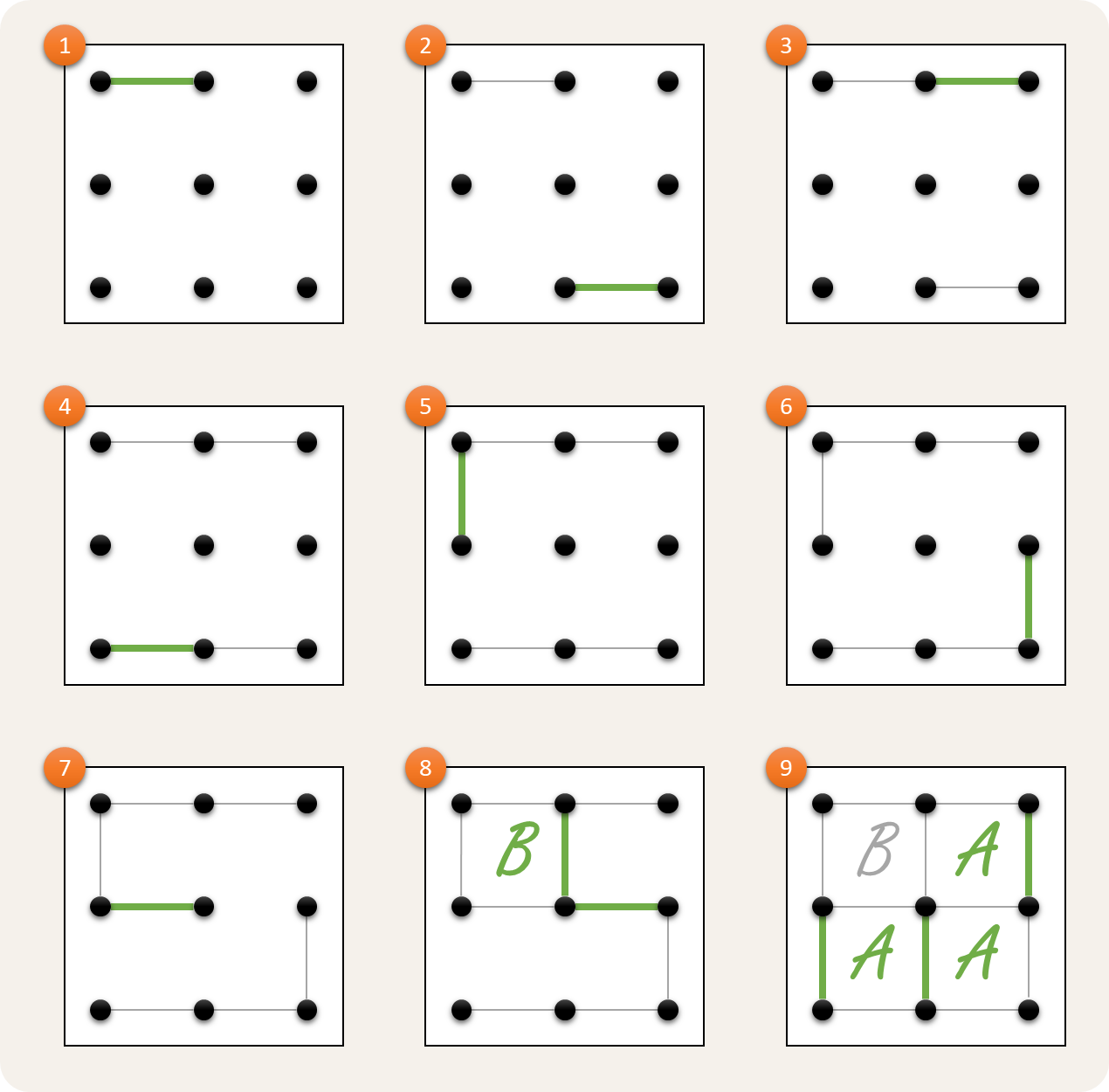
Bovenstaand schema toont het verloop van een spelletje game of dots dat gespeeld wordt op een raster met $$3 \times 3$$ stippen. De tweede speler (B) speelt een geroteerd spiegelbeeld van de lijnen die door de eerste speler (A) getrokken worden, in de hoop het raster in twee stukken te verdelen en zo een gelijkspel uit de wacht te slepen. In stap 7 lijkt speler A zich op te offeren. Speler B aanvaardt het offer en scoort daarmee een punt. Maar nu moet speler B nog een lijn trekken en dus verbindt hij de middenstip met de stip midden rechts. Dit zorgt er echter voor dat de overblijvende $$1 \times 1$$-vakjes een soort ketting vormen, zoals te zien is op het einde van stap 8. In de volgende beurt verovert speler A de drie overblijvende vakjes, waardoor het spel eindigt en speler A wint met 3–1.

Opgave

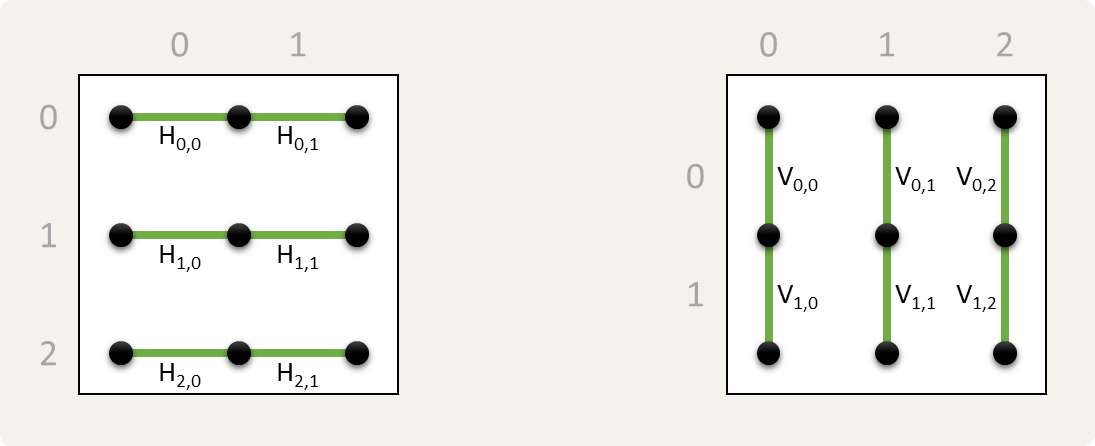
Een spelletje game of dots wordt gespeeld op een $$m \times n$$ raster waarin de stippen gerangschikt worden in $$m$$ rijen en $$n$$ kolommen. De horizontale lijnen die tussen twee aangrenzende stippen kunnen getrokken worden, vormen zelf een $$m \times (n - 1)$$ raster. Als we de rijen van dat raster van boven naar onder nummeren vanaf 0 en de kolommen op dezelfde manier nummeren van links naar rechts, dan kunnen we de positie van een horizontale lijn aanduiden met een string Hr,k. Daarbij stelt $$r \in \mathbb{N}$$ het rijnummer en $$k \in \mathbb{N}$$ het kolomnummer voor. Analoog vormen de verticale lijnen een $$(m - 1) \times n$$ raster en kunnen we de positie van een verticale lijn aanduiden met een string Vr,k.

Stringvoorstelling waarmee de posities van de horizontale en verticale lijnen aangeduid worden.

Ook de vakjes die moeten veroverd worden, vormen een $$(m - 1) \times (n - 1)$$ raster. Als we de rijen van dat raster van boven naar onder nummeren vanaf 0, en de kolommen van links naar rechts, dan gelden de volgende eigenschappen:

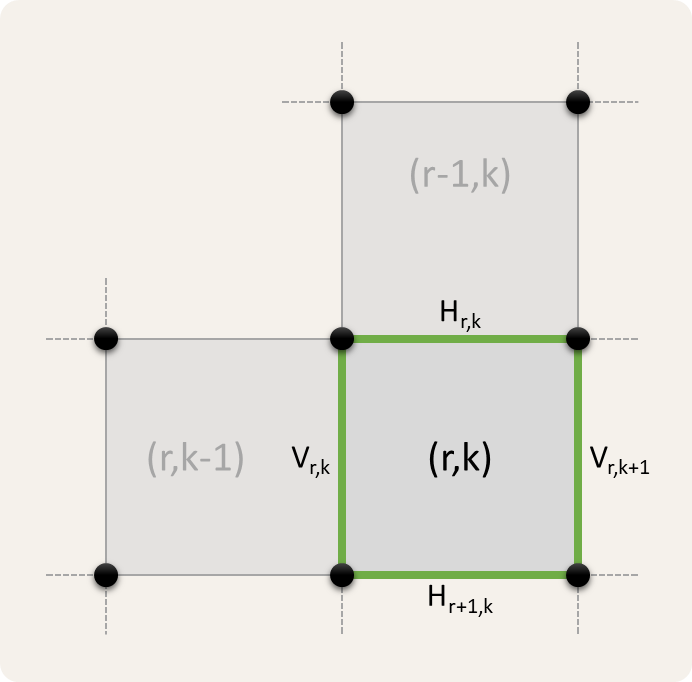
een vakje $$(r, k)$$ op rij $$r$$ en kolom $$k$$ wordt ingesloten door de lijnen $$H_{r, k}$$, $$V_{r, k+1}$$, $$H_{r+1, k}$$ en $$V_{r, k}$$
met een horizontale verbindingslijn $$H_{r,k}$$ kunnen de vakjes $$(r-1, k)$$ en $$(r, k)$$ veroverd worden (als ze bestaan)
met een verticale verbindingslijn $$V_{r,k}$$ kunnen de vakjes $$(r, k-1)$$ en $$(r, k)$$ veroverd worden (als ze bestaan)

Je kunt deze eigenschappen controleren op onderstaande figuur.

Verband tussen de coördinaten van de vakjes die kunnen veroverd worden en de coördinaten van de lijnen die aangrenzende stippen met elkaar verbinden.

Definieer een klasse Pipopipette waarmee een spelletje game of dots kan gespeeld worden tussen twee spelers. Bij het aanmaken van nieuw spelletje (Pipopipette) moeten twee getallen $$m, n \in \mathbb{N}$$ ($$m, n \geq 2$$; Number) doorgegeven worden, die aangeven dat het spelletje op een $$m \times n $$ raster van stippen gespeeld wordt. Als er bij het aanmaken van een spelletje (Pipopipette) slechts één getal $$m$$ wordt doorgegeven, dan wordt het spelletje op een vierkant $$m \times m$$ raster gespeeld.

Voorts moet je op een spelletje $$s$$ (Pipopipette) minstens de volgende methoden kunnen aanroepen:

Een methode score waaraan geen argumenten moeten doorgegeven worden. De methode moet een array (Array) met de huidige score (Number)van de eerste en de tweede speler in spelletje $$s$$ teruggeven.
Een methode toString waaraan geen argumenten moeten doorgeven worden. De methode moet een stringvoorstelling (String) van spelletje $$s$$ teruggeven, die aangeeft welke aangrenzende stippen reeds met elkaar verbonden werden en welke vakjes reeds veroverd werden. De opmaak van de stringvoorstelling kan afgeleid worden uit onderstaand voorbeeld. Hierbij worden de stippen voorgesteld door plus-tekens (+). Horizontale verbindingen tussen twee aangrenzende stippen worden aangeduid met een koppelteken (-), verticale verbindingen met een verticale streep (|) en stippen die nog niet verbonden werden, worden aangeduid met een punt (.). Vakjes die veroverd werden door de eerste speler worden aangeduid met de letter A, vakjes die veroverd werden door de tweede speler met de letter B en vakjes die nog niet veroverd werden met een vraagteken (?).
Een methode player waaraan geen argumenten moeten doorgeven worden. De methode moet een string (String) teruggeven die aangeeft welke speler de volgende lijn mag trekken in spelletje $$s$$: A voor de eerste speler en B voor de tweede speler.
Een methode claim waaraan de positie van een lijn tussen twee aangrenzende stippen (String) moet doorgegeven worden. Als het argument geen geldige positie van een lijn in spelletje $$s$$ voorstelt, dan moet een Error opgeworpen worden met de boodschap invalid position. Als het argument de positie aangeeft van een lijn tussen twee stippen die reeds met elkaar verbonden werden in spelletje $$s$$, dan moet een Error opgeworpen worden met de boodschap dots already connected. Anders moet de methode simuleren dat er op de aangegeven positie een lijn getrokken wordt in spelletje $$s$$. Hierbij moet ook bijgehouden worden welke speler aan de beurt is en welke vakjes de spelers veroverd hebben. De methode moet een verwijzing naar spelletje $$s$$ teruggeven.

Voorbeeld

        > const game = new Pipopipette(3)
> game.score()
[0, 0]
> console.log(game.toString())
+.+.+
.?.?.
+.+.+
.?.?.
+.+.+
> game.player()
"A"
> console.log(game.claim("H0,0").toString())
+-+.+
.?.?.
+.+.+
.?.?.
+.+.+
> game.player()
"B"
> console.log(game.claim("H2,1").toString())
+-+.+
.?.?.
+.+.+
.?.?.
+.+-+
> console.log(game.claim("H0,1").claim("H2,0").toString())
+-+-+
.?.?.
+.+.+
.?.?.
+-+-+
> console.log(game.claim("V0,0").claim("V1,2").claim("H1,0").toString())
+-+-+
|?.?.
+-+.+
.?.?|
+-+-+
> game.player()
"B"
> console.log(game.claim("V0,1").claim("H1,1").toString())
+-+-+
|B|?.
+-+-+
.?.?|
+-+-+
> game.score()
[0, 1]
> game.player()
"A"
> console.log(game.claim("V0,2").claim("V1,1").claim("V1,0").toString())
+-+-+
|B|A|
+-+-+
|A|A|
+-+-+
> game.score()
[3, 1]
> game.claim("ABCD")
Error: invalid position
> game.claim("H10,10")
Error: invalid position
> game.claim("H0,0")
Error: dots already connected