Voor deze uitdaging heb je enkel een kaartspel nodig. Daarmee leg je een willekeurige reeks kaarten voor je op tafel, waarbij sommige kaarten met hun beeldzijde naar boven liggen en de andere kaarten met hun beeldzijde naar onder. Je mag nu elke kaart die met de beeldzijde naar boven ligt verwijderen, maar dan moet je wel de aangrenzende kaarten omkeren (als die er zijn). Het doel is om op die manier alle kaarten te proberen verwijderen. Maar let goed op: als je de verkeerde kaart verwijdert dan zou je wel eens kunnen vastlopen.

We zullen dit eens demonstreren met de onderstaande reeks kaarten. Om alles makkelijker te kunnen uitleggen, nummeren we de kaarten van links naar rechts, te beginnen vanaf nul.

Leg een willekeurig aantal kaarten naast elkaar, waarbij sommige kaarten met hun beeldzijde naar boven liggen en de andere met hun beeldzijde naar onder.

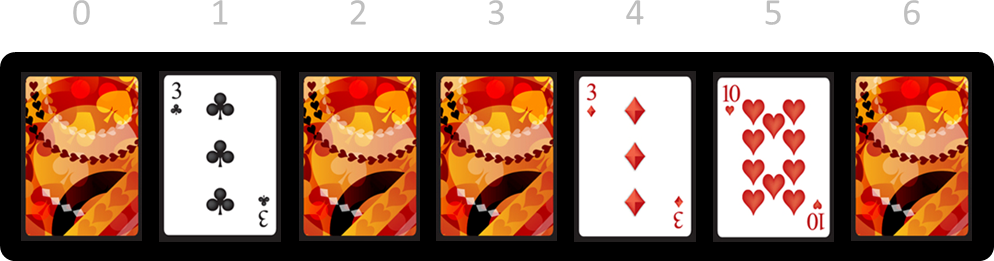
Je kan nu kiezen om kaarten 1, 4 of 5 te verwijderen, omdat die met hun beeldzijde naar boven liggen. Als je kaart 1 verwijdert, dan ziet de reeks kaarten er daarna als volgt uit (het rode kruisje geeft de positie van de kaart aan die we zopas verwijderd hebben).

Verwijder kaart 1 en keer de twee aangrenzende kaarten 0 en 2 om.

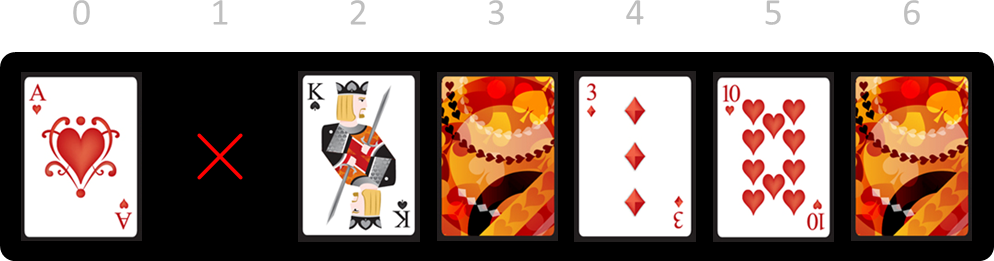
Daarbij moest je kaarten 0 en 2 omkeren omdat ze naast kaart 1 liggen. Vervolgens kan je kiezen om kaarten 0, 2, 4 of 5 te verwijderen. Stel dat je kaart 0 verwijdert.

Verwijder kaart 0. Omdat er naast die kaart geen andere kaarten liggen, moet je dus ook geen kaarten omkeren.

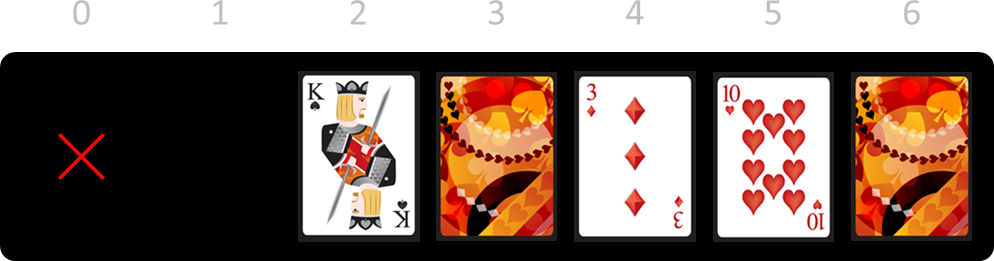
Omdat kaart 0 geen aangrenzende kaarten heeft, moet je in dit geval geen kaarten omkeren. Je kan het spel winnen door nu achtereenvolgens kaarten 2, 3, 5, 4 en 6 te verwijderen.

Je kan het spel winnen door nu achtereenvolgens kaarten 2, 3, 5, 4 en 6 te verwijderen.

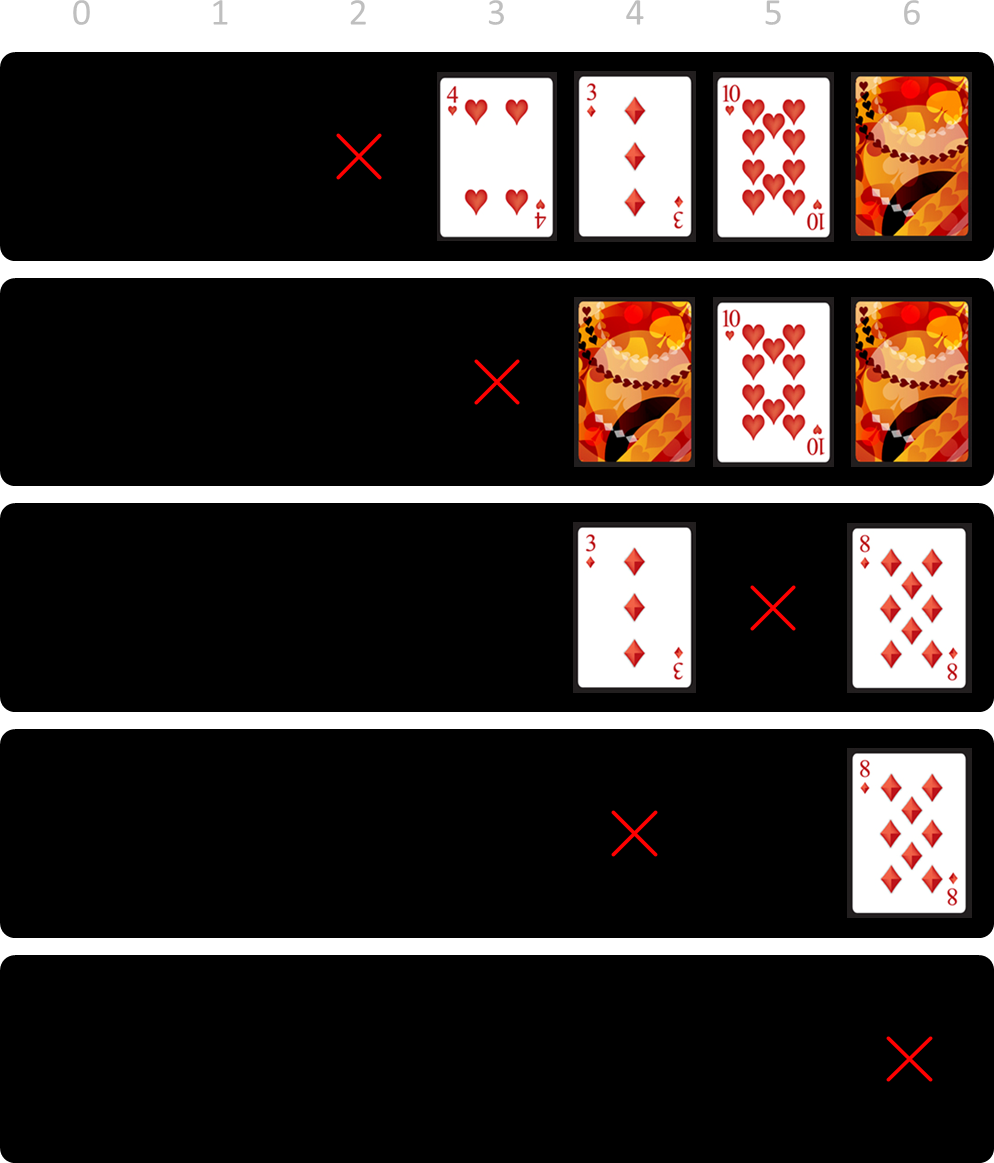
Dit lukt echter niet altijd. Stel dat je begonnen was met het verwijderen van kaart 4.

Verwijder kaart 4 en keer de twee aangrenzende kaarten 3 en 5 om.

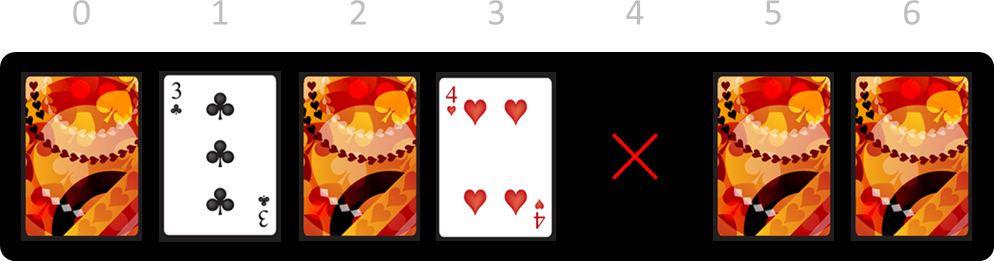
Met deze reeks kaarten kan je niet meer winnen, omdat er rechts een "eiland" van kaarten is ontstaan die allemaal met hun beeldzijde naar onder liggen. Kaarten op zo'n eiland kunnen nooit met hun beeldzijde naar boven gedraaid worden, waardoor ze ook niet kunnen verwijderd worden.

Opgave

Een standaard kaartspel bestaat uit 52 verschillende kaarten die onderverdeeld worden in vier kleuren van elk 13 kaarten: 13 klaveren (♣), 13 ruiten (♦), 13 harten (♥) en 13 schoppen (♠). Klaveren en schoppen zijn zwart, ruiten en harten zijn rood, maar het zijn niet deze fysieke kleuren, maar de soorten die met de term kleur aangeduid worden. Van elke kleur zijn er telkens kaarten met een rang van 2 tot en met 10, een boer, een vrouw, een heer en een aas. Daarnaast bevat een spel soms twee of drie jokers, maar die laten we hier even buiten beschouwing.

We stellen elk van de 52 kaarten van een standaard kaartspel voor als een string (str) die bestaat uit de rang van de kaart, gevolgd door de kleur van de kaart:

rangen: 2, 3, 4, 5, 6, 7, 8, 9, 10, J (boer), Q (vrouw), K (heer) en A (aas)
kleuren: C (klaveren; ♣), D (ruiten; ♦), H (harten; ♥) en S (schoppen; ♠)

Zo stelt AS bijvoorbeeld schoppenaas voor, 10H hartentien en KC klaverenheer. Bovendien leggen we vast dat de voorstelling van een kaart die met zijn beeldzijde naar boven ligt gebruik maakt van hoofdletters (bijvoorbeeld AS of 10H), en dat de voorstelling van een kaart die met zijn beeldzijde naar onder ligt gebruik maakt van kleine letters (bijvoorbeeld as of 10h). Merk op dat het laatste karakter van de voorstelling altijd een hoofdletter of een kleine letter is (geen cijfer) die de kleur van de kaart aanduidt.

Definieer een klasse Kaarten waarmee een reeks kaarten kan voorgesteld worden, waarbij sommige kaarten met hun beeldzijde naar boven en de andere met hun beeldzijde naar onder liggen. Een reeks kaarten hoeft niet noodzakelijk alle 52 kaarten van een kaartspel te bevatten, maar elke kaart mag hoogstens één keer voorkomen. Bij het aanmaken van een object van de klasse Kaarten moet een reeks (list of tuple) met stringvoorstellingen van kaarten doorgegeven worden. Indien geen geldige reeks kaarten wordt doorgegeven, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige kaarten.

Zorg ervoor dat de conversie van een object $$o$$ van de klasse Kaarten naar een string — bekomen met de ingebouwde functie str — een reeks kaarten voorstelt zoals aangegeven in onderstaande voorbeeldsessie. Dit bestaat uit de voorstellingen van de opeenvolgende kaarten van de reeks, telkens van elkaar gescheiden door een spatie. Hierbij wordt een kaart die met zijn beeldzijde naar boven ligt op de standaard manier voorgesteld. Een kaart die met zijn beeldzijde naar onder ligt wordt voorgesteld door twee sterretjes (**). Een verwijderde kaart wordt voorgesteld door een groter dan-teken, gevolgd door een kleiner dan-teken (><).

Voorts moet de klasse Kaarten minstens de volgende methoden ondersteunen:

Een methode verwijder waaraan ofwel het volgnummer (int) of de stringvoorstelling (str) moet doorgegeven worden van een kaart uit de reeks die met zijn beeldzijde naar boven ligt. Als het gegeven argument geen kaart aanduidt die met zijn beeldzijde naar boven ligt, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige kaart. Anders moet de kaart verwijderd worden, en moeten de twee aangrenzende kaarten omgekeerd worden (als die er zijn). De methode moet een verwijzing teruggeven naar het object waarop de methode werd aangeroepen.
Een methode eilanden waaraan geen argumenten moeten doorgegeven worden. De methode moet teruggeven hoeveel eilanden gevormd worden door de kaarten die nog niet verwijderd werden. Hierbij is een eiland de langst mogelijke reeks van naburige kaarten, zonder tussenliggende posities waar kaarten verwijderd werden.
Een methode isgewonnen waaraan geen argumenten moeten doorgegeven worden. De methode moet een Booleaanse waarde (bool) teruggeven, die aangeeft of het spel gewonnen werd. Dat is het geval als alle kaarten konden verwijderd worden.

Voorbeeld

        >>> kaarten = Kaarten(['ah', '3S', 'kc', '4h', '3D', '10H', '8d'])
>>> print(kaarten)
** 3S ** ** 3D 10H **
>>> kaarten.eilanden()
1
>>> kaarten.isgewonnen()
False
>>> print(kaarten.verwijder(1))
AH >< KC ** 3D 10H **
>>> kaarten.verwijder(1)
Traceback (most recent call last):
AssertionError: ongeldige kaart
>>> kaarten.verwijder(3)
Traceback (most recent call last):
AssertionError: ongeldige kaart
>>> kaarten.verwijder(-3)
Traceback (most recent call last):
AssertionError: ongeldige kaart
>>> kaarten.verwijder(42)
Traceback (most recent call last):
AssertionError: ongeldige kaart
>>> print(kaarten.verwijder('AH'))
>< >< KC ** 3D 10H **
>>> kaarten.eilanden()
1
>>> kaarten.isgewonnen()
False
>>> print(kaarten.verwijder('AH'))
Traceback (most recent call last):
AssertionError: ongeldige kaart
>>> print(kaarten.verwijder('QS'))
Traceback (most recent call last):
AssertionError: ongeldige kaart
>>> print(kaarten.verwijder(2).verwijder(3))
>< >< >< >< ** 10H **
>>> kaarten.eilanden()
1
>>> kaarten.isgewonnen()
False
>>> print(kaarten.verwijder('10h').verwijder('3d').verwijder('8d'))
>< >< >< >< >< >< ><
>>> kaarten.eilanden()
0
>>> kaarten.isgewonnen()
True

>>> Kaarten(['ah', '3S', 'kc', '4h', '3D', 'AH', '8d'])
Traceback (most recent call last):
AssertionError: ongeldige kaarten
>>> Kaarten(['ah', '3S', 'kc', '4h', '3D', 42, '8d'])
Traceback (most recent call last):
AssertionError: ongeldige kaarten
>>> Kaarten(['ah', '3S', 'kc', '4h', '3D', 'XD', '8d'])
Traceback (most recent call last):
AssertionError: ongeldige kaarten
>>> Kaarten(['ah', '3S', 'kc', '4h', '3D', 'AY', '8d'])
Traceback (most recent call last):
AssertionError: ongeldige kaarten
>>> Kaarten({'ah', '3S', 'kc', '4h', '3D', '10H', '8d'})
Traceback (most recent call last):
AssertionError: ongeldige kaarten