Permutatie test

Onder \(H_0\) zijn de bloeddrukmetingen voor en na toediening van captopril twee “base line” bloeddrukmetingen voor een patiënt
Onder \(H_0\) kunnen we de bloeddrukmetingen voor iedere patiënt in willekeurige volgorde plaatsen (permuteren).

set.seed(35)
captoprilSamp <- captopril
perm <- sample(c(FALSE, TRUE), 15, replace = TRUE)
captoprilSamp$SBPa[perm] <- captopril$SBPb[perm]
captoprilSamp$SBPb[perm] <- captopril$SBPa[perm]
captoprilSamp$deltaSBP <- captoprilSamp$SBPa-captoprilSamp$SBPb
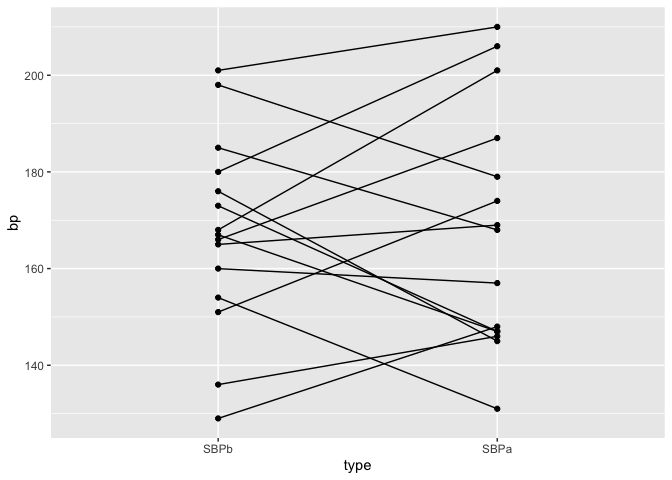
captoprilSamp %>%
  gather(type, bp, -id) %>%
  filter(type %in% c("SBPa","SBPb")) %>%
  mutate(type = factor(type, levels = c("SBPb", "SBPa")))%>%
  ggplot(aes(x = type,y = bp)) +
  geom_line(aes(group = id)) +
  geom_point()

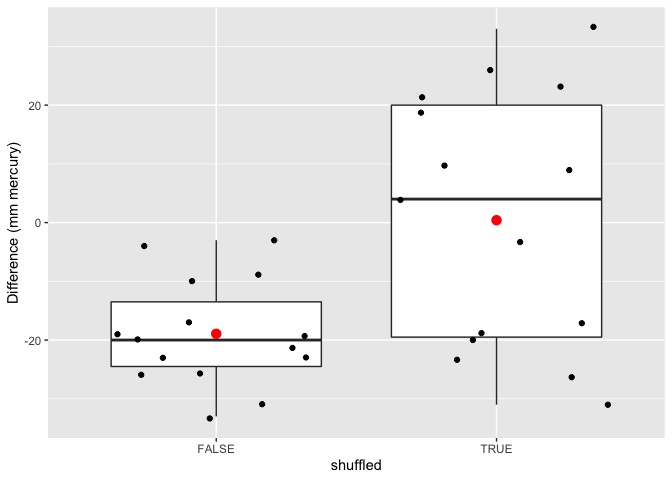
data.frame(
  deltaSBP = c(captopril$deltaSBP,captoprilSamp$deltaSBP),
  shuffled=rep(c(FALSE,TRUE),each=15)
  ) %>%
  ggplot(aes(x = shuffled, y = deltaSBP)) +
  geom_boxplot(outlier.shape = NA) +
  geom_point(position = "jitter")+
  stat_summary(
    fun.y = mean,
    geom = "point",
    shape = 19,
    size = 3,
    color = "red",
    fill = "red") +
  ylab("Difference (mm mercury)")

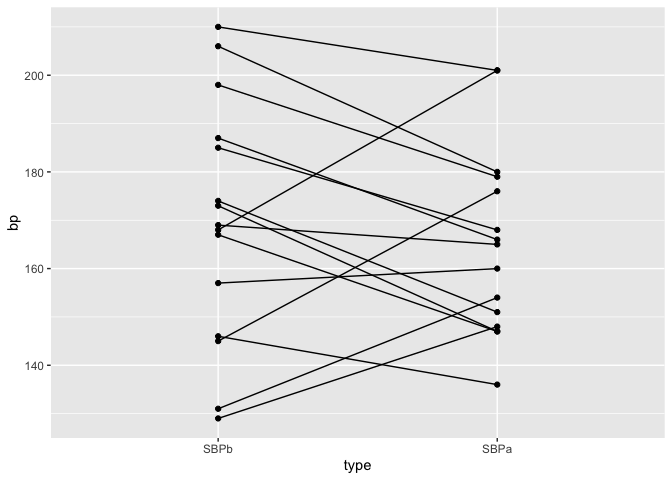
We permuteren opnieuw

captoprilSamp <- captopril
perm <- sample(c(FALSE,TRUE), 15, replace = TRUE)
captoprilSamp$SBPa[perm] <- captopril$SBPb[perm]
captoprilSamp$SBPb[perm] <- captopril$SBPa[perm]
captoprilSamp$deltaSBP <- captoprilSamp$SBPa-captoprilSamp$SBPb
captoprilSamp %>%
  gather(type, bp, -id) %>%
  filter(type %in% c("SBPa","SBPb")) %>%
  mutate(type = factor(type, levels = c("SBPb", "SBPa")))%>%
  ggplot(aes(x = type,y = bp)) +
  geom_line(aes(group = id)) +
  geom_point()

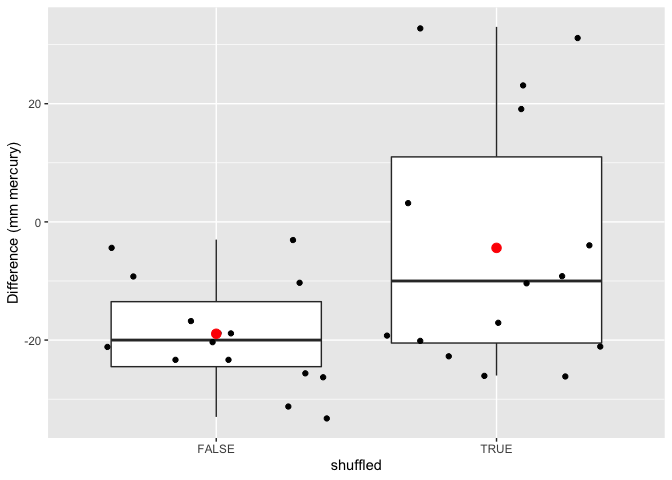
data.frame(
  deltaSBP = c(captopril$deltaSBP,captoprilSamp$deltaSBP),
  shuffled=rep(c(FALSE,TRUE),each=15)
  ) %>%
  ggplot(aes(x = shuffled, y = deltaSBP)) +
  geom_boxplot(outlier.shape = NA) +
  geom_point(position = "jitter")+
  stat_summary(
    fun.y = mean,
    geom = "point",
    shape = 19,
    size = 3,
    color = "red",
    fill = "red") +
  ylab("Difference (mm mercury)")

Er zijn \(2^{15}\) = 32768 mogelijke permutaties!
We hoeven in principe alleen de tekens van de waargenomen bloeddrukverschillen \(x\) te wisselen als we permuteren.

permH <- expand.grid(
  replicate(
    15,
    c(-1,1),
    simplify=FALSE)
  ) %>%
  t

permH[,1:5]

##       [,1] [,2] [,3] [,4] [,5]
## Var1    -1    1   -1    1   -1
## Var2    -1   -1    1    1   -1
## Var3    -1   -1   -1   -1    1
## Var4    -1   -1   -1   -1   -1
## Var5    -1   -1   -1   -1   -1
## Var6    -1   -1   -1   -1   -1
## Var7    -1   -1   -1   -1   -1
## Var8    -1   -1   -1   -1   -1
## Var9    -1   -1   -1   -1   -1
## Var10   -1   -1   -1   -1   -1
## Var11   -1   -1   -1   -1   -1
## Var12   -1   -1   -1   -1   -1
## Var13   -1   -1   -1   -1   -1
## Var14   -1   -1   -1   -1   -1
## Var15   -1   -1   -1   -1   -1

We zullen dit voor alle mogelijke permutaties doen en we zullen het gemiddelde bijhouden.

#calculate the means for the permuted data
muPerm <- colMeans(permH*captopril$deltaSBP)
muPerm %>%
  as.data.frame %>%
  ggplot(aes(x=.)) +
  geom_histogram() +
  geom_vline(
    xintercept = mean(captopril$deltaSBP),
    col = "blue")

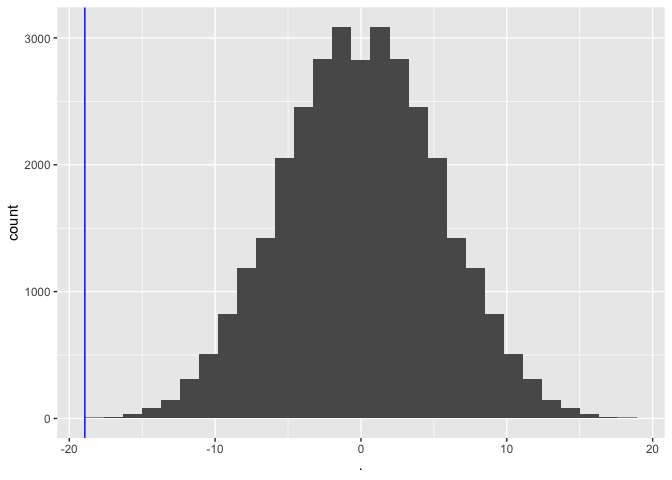
sum(muPerm <= mean(captopril$deltaSBP))

## [1] 1

mean(muPerm <= mean(captopril$deltaSBP))

## [1] 3.051758e-05

We zien dat maar 1 van de gemiddelden die werden verkregen onder \(H_0\) (door permutatie) zo extreem was als het steekproefgemiddelde dat we in de captopril-studie hebben waargenomen.
Dus de kans om een bloeddrukdaling waar te nemen die groter of gelijk is dan die in de captopril-studie in een willekeurige steekproef onder de nulhypothese, is 1 op de 32768.

We hebben dus sterk bewijs dat \(H_0\) onjuist is en daarom verwerpen we \(H_0\) en concluderen \(H_1\): het toedienen van captopril heeft een effect op de bloeddruk van patiënten met hypertensie.

Pivot

In de praktijk gebruiken we altijd statistieken die de effectgrootte (gemiddeld verschil) afwegen tegen ruis (standaard error)
Als we de nulhypothese ontkrachten, standaardiseren we het gemiddelde rond \(\mu_0 = 0\) het gemiddelde onder \(H_0\)

\[t=\frac{\bar X-\mu_0}{se_{\bar X}}\]

Voor het Captopril voorbeeld wordt dit:

\[\frac{-18.93-0}{2.33}=-8.12\]

We bepalen nu de nulverdeling van teststatistiek t met permutatie.

deltaPerms <- permH*captopril$deltaSBP
tPerm <- colMeans(deltaPerms)/(apply(deltaPerms,2,sd)/sqrt(15))
tOrig <- mean(captopril$deltaSBP)/sd(captopril$deltaSBP)*sqrt(15)

tPermPlot <- tPerm %>%
  as.data.frame %>%
  ggplot(aes(x = .)) +
  geom_histogram(aes(y = ..density.., fill = ..count..)) +
  geom_vline(xintercept = tOrig,col = "blue")
tPermPlot

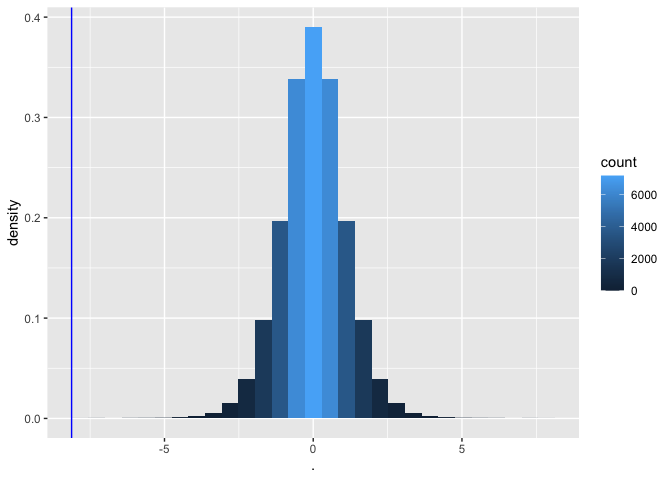
Opnieuw heeft slechts 1 van de permutaties een t-statistiek die zo extreem is als de statistiek die wordt waargenomen in de captopril-studie.

Wanneer er geen effect is van captopril, is het bijna onmogelijk om een teststatistiek te verkrijgen die zo extreem is als degene die werd waargenomen in de steekproef (t=-8.12).

De kans om een grotere bloeddrukdaling waar te nemen dan degene die we in onze steekproef hebben waargenomen in een willekeurige steekproef onder \(H_0\) is 1/32768.
We noemen deze kans de p-waarde.
Het meet de sterkte van het bewijs tegen de nulwaarde: hoe kleiner de p-waarde, hoe meer bewijs we hebben dat de nulwaarde niet waar is.
De verdeling heeft een mooie klokvorm.

Hoe beslissen we?

Wanneer is de p-waarde klein genoeg om te concluderen dat er sterk bewijs is tegen de nulhypothese?

We werken doorgaans met een significantieniveau van \(\alpha = 0,05\)
We stellen dat we de test hebben uitgevoerd op het significantieniveau van 5%

Permutatietests zijn computationeel veeleisend

Kunnen we beoordelen hoe extreem de bloeddrukdaling was zonder permutatie?
We weten dat de bloeddrukverschillen ongeveer normaal verdeeld zijn, dus

\[t=\frac{\bar X - \mu}{se_{\bar X}}\]

volgt een t-verdeling (met 14 vrijheidsgraden voor het Captopril voorbeeld).

Onder \(H_0\) \(\mu=0\) en

\[t=\frac{\bar X-0}{se_{\bar X}}\sim f_{T,14}\]

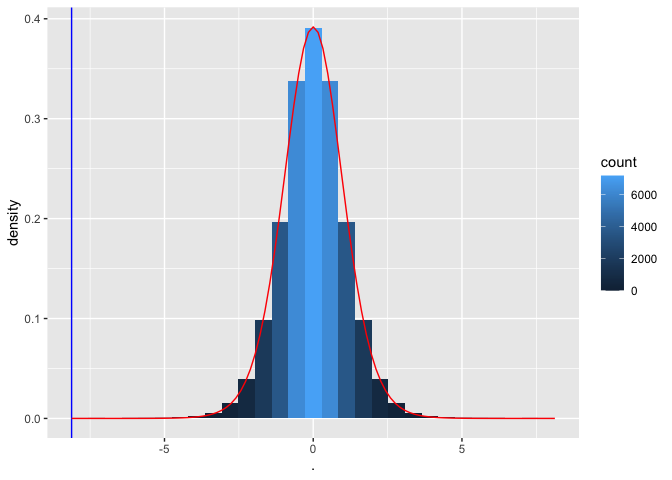
tPermPlot +
  stat_function(
    fun = dt,
    color = "red",
    args = list(df=14))

Merk op dat de permutatie-nulverdeling inderdaad overeenkomt met een t-verdeling met 14 vrijheidsgraden.
Zodat we de statistische test kunnen uitvoeren met behulp van statistische modellen van de gegevens.
Hiervoor moeten we assumpties maken, die we verifiëren in de data exploratie.

We overlopen nu alle componenten van een hypothese test waarbij we gebruik maken van veronderstellingen over de distributie van de gegevens.