Calculating the validation errors manually was a little tedious, partly because there is no predict() method for regsubsets(). Since we will be using this function again, we can capture our steps above and write our own predict method.

predict.regsubsets <- function(object, newdata, id, ...) {
  mat <- model.matrix(Salary ~ ., data = newdata) # change the dependent variable for other data
  coefi <- coef(object, id = id)
  xvars <- names(coefi)
  mat[, xvars] %*% coefi
}

Our function pretty much mimics what we did in the previous exercise. The only complex part is how we extracted the formula used in the call to regsubsets(). We demonstrate how we use this function below, when we do cross-validation.

Finally, we perform best subset selection on the full data set, and select the best ten-variable model. It is important that we make use of the full data set in order to obtain more accurate coefficient estimates. Note that we perform best subset selection on the full data set and select the best ten-variable model, rather than simply using the variables that were obtained from the training set, because the best ten-variable model on the full data set may differ from the corresponding model on the training set.

> regfit.best <- regsubsets(Salary ~ ., data = Hitters, nvmax = 19)
> coef(regfit.best, 10)
 (Intercept)        AtBat         Hits        Walks 
 162.5354420   -2.1686501    6.9180175    5.7732246 
      CAtBat        CRuns         CRBI       CWalks 
  -0.1300798    1.4082490    0.7743122   -0.8308264 
   DivisionW      PutOuts      Assists 
-112.3800575    0.2973726    0.2831680

In fact, we see that the best ten-variable model on the full data set has a different set of variables than the best ten-variable model on the training set.

We now try to choose among the models of different sizes using cross-validation. This approach is somewhat involved, as we must perform best subset selection within each of the \(k\) training sets. Despite this, we see that with its clever subsetting syntax, R makes this job quite easy. First, we create a vector that allocates each observation to one of \(k = 10\) folds, and we create a matrix in which we will store the results.

k <- 10
set.seed(1)
folds <- sample(1:k, nrow(Hitters), replace = TRUE)
cv.errors <- matrix(NA, k, 19, dimnames = list(NULL, paste(1:19)))

Now we write a for loop that performs cross-validation. In the \(j\)th fold, the elements of folds that equal \(j\) are in the test set, and the remainder are in the training set. We make our predictions for each model size (using our new predict() method), compute the test errors on the appropriate subset, and store them in the appropriate slot in the matrix cv.errors.

for (j in 1:k) {
  best.fit <- regsubsets(Salary ~ ., data = Hitters[folds != j,], nvmax = 19)
  for (i in 1:19) {
    pred <- predict(best.fit, Hitters[folds == j,], id = i)
    cv.errors[j, i] <- mean((Hitters$Salary[folds == j] - pred)^2)
  }
}

This has given us a 10×19 matrix, of which the \((i, j)\)th element corresponds to the test \(MSE\) for the \(i\)th cross-validation fold for the best \(j\)-variable model. We use the apply() function to average over the columns of this matrix in order to obtain a vector for which the \(j\)th element is the cross-validation error for the \(j\)-variable model.

> mean.cv.errors <- apply(cv.errors, 2, mean)
> mean.cv.errors
       1        2        3        4        5        6 
149821.1 130922.0 139127.0 131028.8 131050.2 119538.6 
       7        8        9       10       11       12 
124286.1 113580.0 115556.5 112216.7 113251.2 115755.9 
      13       14       15       16       17       18 
117820.8 119481.2 120121.6 120074.3 120084.8 120085.8 
      19 
120403.5 
> par(mfrow = c(1, 1))
> plot(mean.cv.errors, type = 'b')

plot

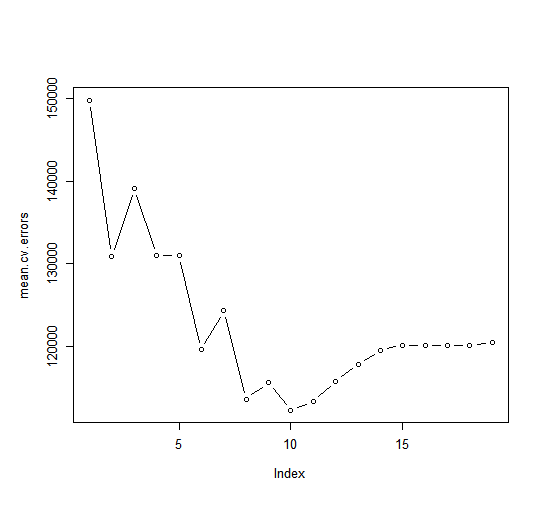
We see that cross-validation selects an 10-variable model. We now perform best subset selection on the full data set in order to obtain the 10-variable model.

> reg.best <- regsubsets(Salary ~ ., data = Hitters, nvmax = 19)
> coef(reg.best, 10)
 (Intercept)        AtBat         Hits        Walks       CAtBat        CRuns    
 162.5354420   -2.1686501    6.9180175    5.7732246   -0.1300798    1.4082490     
        CRBI       CWalks    DivisionW      PutOuts      Assists 
   0.7743122   -0.8308264 -112.3800575    0.2973726    0.2831680

Questions

Note: The Hitters dataset has 19 predictors, the Boston dataset has only 13.

Assume that: