Er is iets heel bijzonder aan deze drie reeksen van tien cijfers.

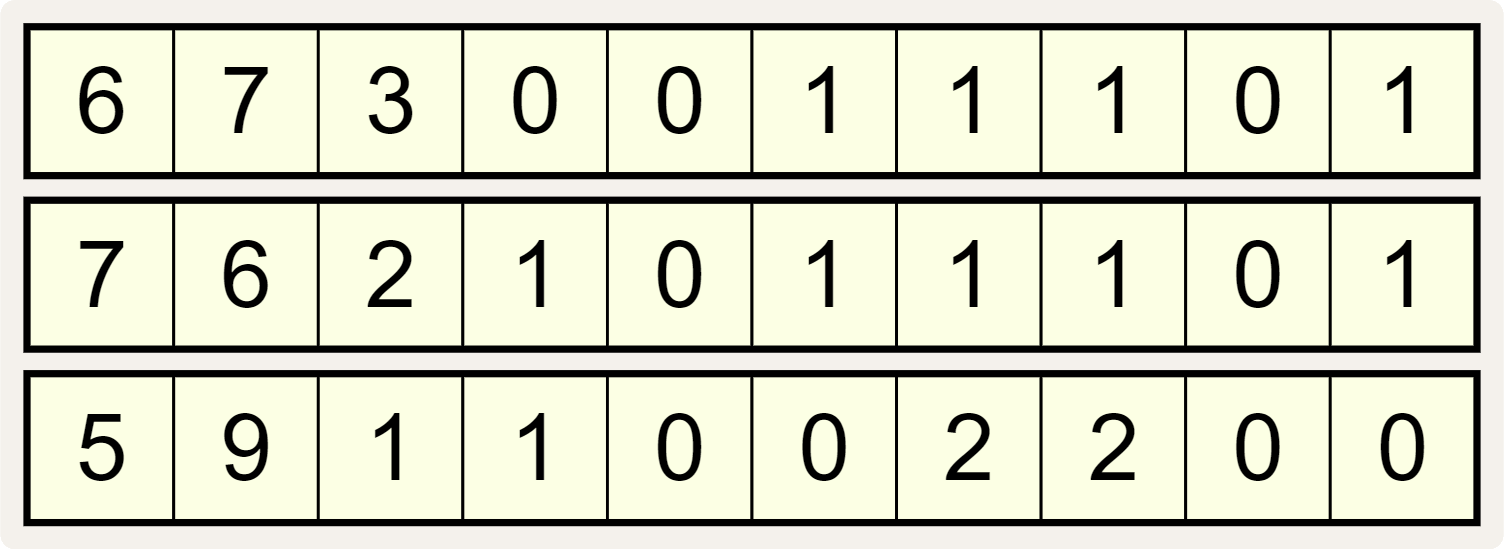
Als we de posities van de cijfers in elke reeks van links naar rechts nummeren vanaf 0 — zoals aangegeven met de grijze cijfers in de hoofding van onderstaande voorstelling van de drie cijferreeksen — dan geeft elk cijfer in kolom $$i$$ ($$i = 0, 1, \ldots, 9)$$ van een cijferreeks aan hoeveel keer het cijfer $$i$$ voorkomt in de twee andere reeksen.

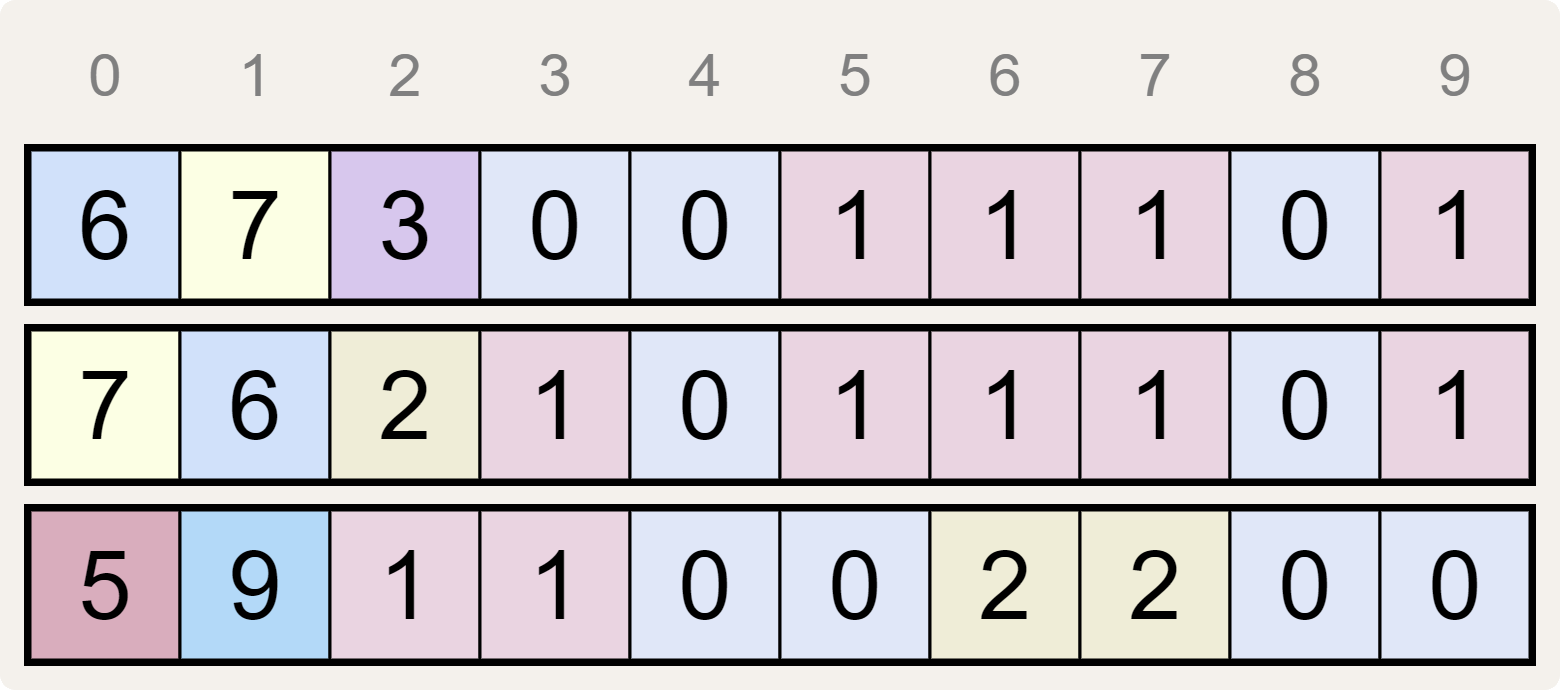
Zo geeft het cijfer 6 aan de linkerkant van de bovenste cijferreeks bijvoorbeeld aan dat het cijfer 0 in totaal 6 keer voorkomt in de onderste twee cijferreeksen. Deze elegante eigenschap geldt ook voor alle andere cijfers in elk van de drie cijferreeksen.

De elegante eigenschap geldt echter niet zomaar voor elke combinatie van drie reeksen met tien cijfers. Als we bijvoorbeeld deze drie cijferreeksen nemen

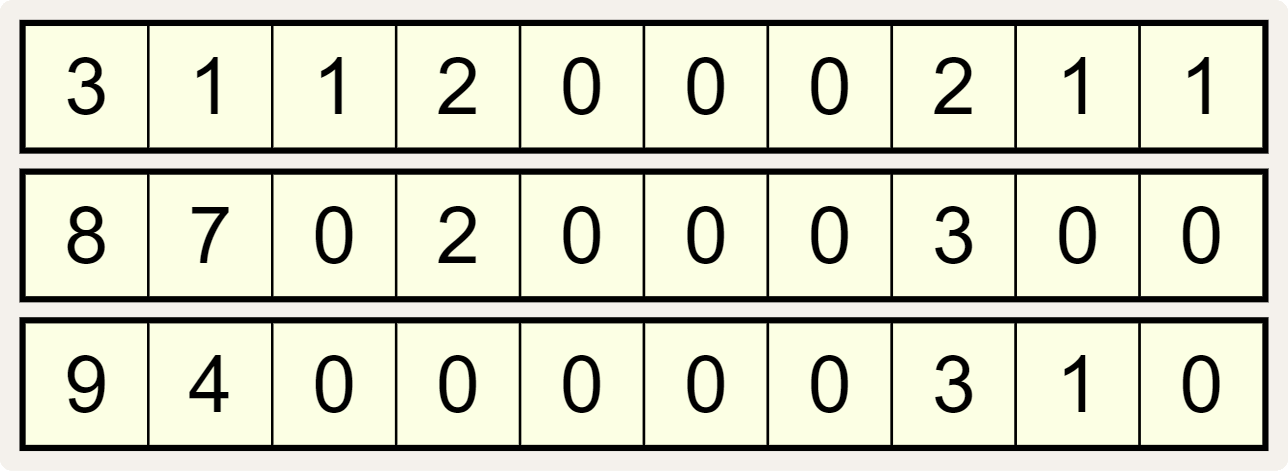
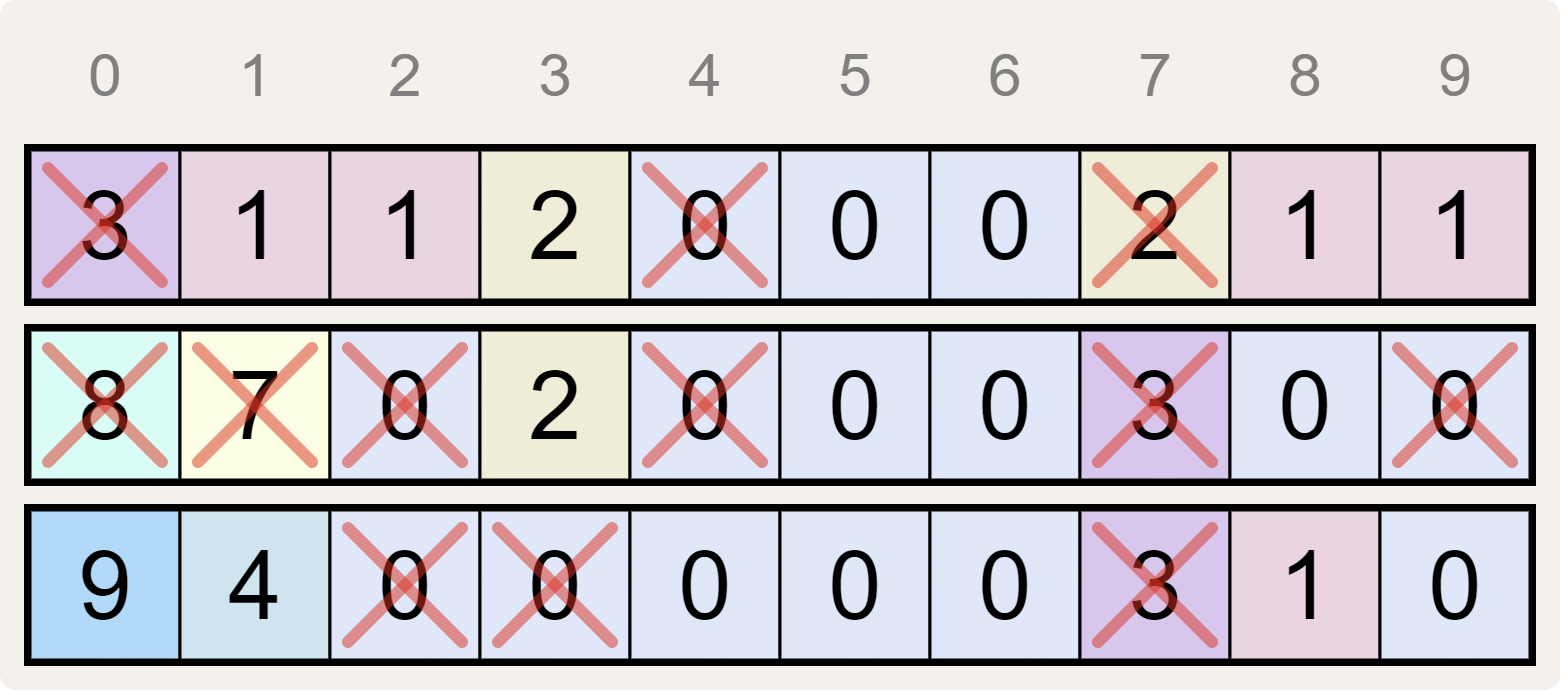
dan hebben we hieronder een rood kruis getrokken door elk cijfer dat niet overeenkomt met het aantal keer dat het cijfer $$i$$ ($$i = 0, 1, \ldots, 9$$) van de corresponderende kolom voorkomt in de andere twee cijferreeksen.

Opgave

Het Unix commando dat we hieronder reeds gedeeltelijk opgesteld hebben, schrijft voorlopig twee reeksen van 10 cijfers naar stdout.

$ echo "7621011101" "5911002200" | …

Vul het commando verder aan zodat het in plaats daarvan een regel uitschrijft naar stdout met een derde reeks van 10 cijfers, waarvan elk cijfer aangeeft hoeveel keer het cijfer $$i$$ ($$i = 0, 1, \ldots, 9$$) van de corresponderende kolom voorkomt in de twee gegeven cijferreeksen. Zorg ervoor dat je aanvulling ook het gevraagde resultaat blijft weergeven als de twee gegeven reeksen van 10 cijfers wijzigen. Je mag ervan uitgaan dat elk cijfer hoogstens 9 keer in de twee gegeven cijferreeksen voorkomt.

Voorbeeld

$ echo "7621011101" "5911002200" | …
6730011101
$ echo "6730011101" "7621011101" | …
5911002200
$ echo "6730011101" "5911002200" | …
7621011101

Oplossingsstrategie

Dit is een mogelijke strategie dit je kunt gebruiken om deze opgave op te lossen. We gebruiken het voorbeeld uit de opgave als illustratie.

1. Bepaal hoeveel keer elk cijfer (0–9) voorkomt in de twee gegeven cijferreeksen van 10 cijfers en in de extra cijferreeks 0123456789 die elk cijfer juist één keer bevat. Die extra cijferreeks zorgt ervoor dat elk cijfer minstens één keer voorkomt in de drie reeksen. Dit is het histogram dat we bekomen voor de twee voorbeeldreeksen (en de extra reeks):

   cijfer	# voorkomens
   0	7
   1	8
   2	4
   3	1
   4	1
   5	2
   6	2
   7	2
   8	1
   9	2

2. Zorg ervoor dat het histogram (zoals hierboven) het aantal voorkomens oplijst in oplopende volgorde van de cijferwaarden (0–9). Behoud uit het histogram enkel de kolom met het aantal voorkomens.

   # voorkomens
   7
   8
   4
   1
   1
   2
   2
   2
   1
   2

3. Verminder het aantal voorkomens met 1. Dit doet de inbreng van de extra cijferreeks 0123456789 teniet, maar die reeks zorgt er wel voor dat we voor elk cijfer (0–9) het aantal voorkomens bepaald hebben — ook voor de cijfers die niet in de twee gegeven cijferreeksen voorkomen.

   # voorkomens
   6
   7
   3
   0
   0
   1
   1
   1
   0
   1

4. Zet het aantal voorkomens (van boven naar onder) achter elkaar. Dit levert de reeks van 10 cijfers op die we zoeken: 6730011101.

Richtlijnen bij het indienen

Dien enkel het stuk van het commando in dat moet ingevuld worden op de plaats van de drie puntjes (…).