Het vermoeden van Collatz is afkomstig uit de getaltheorie. Het is gebaseerd op een specifieke reeks — een hagelsteen-reeks¹ genoemd — die als volgt geconstrueerd wordt:

• Neem een willekeurig natuurlijk getal $$n$$.
• Als $$n$$ even is, dan wordt het gedeeld door 2.
• Als $$n$$ oneven is, dan wordt het vermenigvuldigd met 3 en wordt daar nog 1 bij opgeteld.

Het vermoeden van Collatz zegt nu dat voor elk natuurlijk getal $$n$$ ($$n ≥ 1$$) de corresponderende hagelsteen-reeks altijd eindigt bij 1, als je het beschreven proces maar lang genoeg herhaalt. Dit vermoeden werd voor het eerst geformuleerd door Lothar Collatz in 1937. Tot op heden is het vermoeden nog niet bevestigd of weerlegd.

Stel dat we bijvoorbeeld vertrekken van het getal $$n=12$$, dan ziet de corresponderende hagelsteen-reeks er als volgt uit:

12, 6, 3, 10, 5, 16, 8, 4, 2, 1

Men zegt dat de cyclelengte voor $$n=12$$ gelijk is aan 10, omdat de lengte van de bijhorende hagelsteen-reeks (inclusief de laatste waarde 1) gelijk is aan 10. Als we echter vertrekken van het getal $$n=15$$, dan ontstaat een veel langere reeks met cyclelengte 18:

15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1

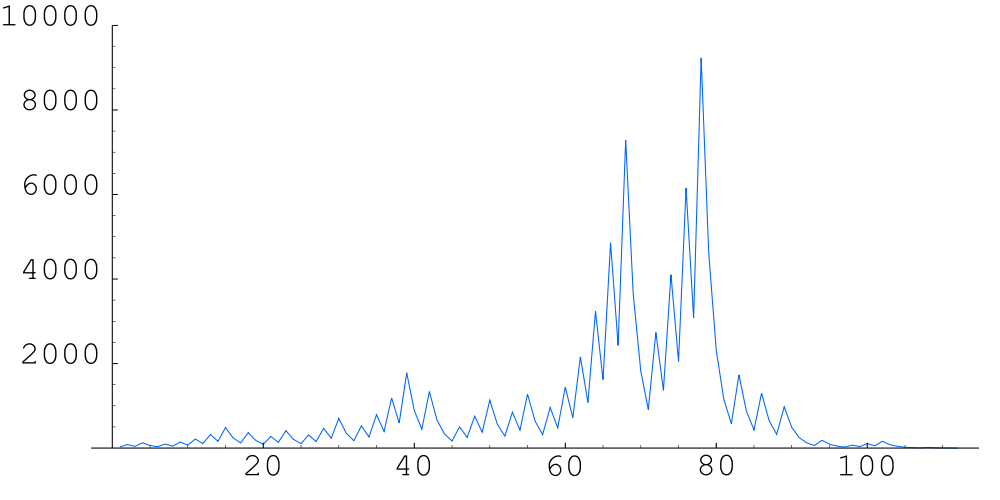
Voor $$n=27$$ loopt de cyclelengte op tot 112, waarbij een maximale waarde bereikt wordt die al eens stuk boven de 9000 ligt:

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1

Onderstaande grafiek illustreert het verloop van de hagelsteen-reeks voor $$n=27$$.

Opgave

In deze opgave gaan we de cyclelengte van een hagelsteen-reeks berekenen voor $$n \in \mathbb{N}_{0}$$

• Schrijf een functie volgend_collatz_getal die gegeven een getal $$n$$ het volgende getal in de hagelsteen-reeks berekent.
• Schrijf een functie collatz die gegeven een getal $$n$$ de cyclelengte van de hagelsteenreeks berekent. Maak in deze functie gebruik van de functie volgend_collatz_getal.

Voorbeeld

>>> volgend_collatz_getal(12)
6
>>> volgend_collatz_getal(27)
82
>>> volgend_collatz_getal(321)
964

>>> collatz(12)
10
>>> collatz(27)
112
>>> collatz(321)
25