Binomiale test

Om een toets te kunnen construeren van de nulhypothese dat

\[H_0: \pi=1/2 \text{ versus } H_1: \pi\neq 1/2,\]

moeten we de verdeling van de gegevens \(X\) en van de schatter voor de proportie, \(\hat \pi = \bar X\) (of equivalent de som \(S=n\bar X\)) kennen.

Stel dat het voorkomen van jongens en meisjes in de populatie even waarschijnlijk zijn; m.a.w. stel dat de nulhypothese waar is. Bij lukrake trekking van één individu uit de populatie is de kans dat men een jongen observeert dan gelijk aan \(P(X=1) = \pi = 1/2.\) Als twee kinderen onafhankelijk van elkaar getrokken worden (en de populatie is bij benadering oneindig groot) dan heeft zowel het eerste als het tweede kind kans 1/2 om mannelijk te zijn (onafhankelijk van elkaar). De uitkomsten \((x_1, x_2)\) voor beide kinderen hebben dan 4 mogelijke waarden: \((0,0), (0,1),(1,0)\) en \((1,1).\) Deze komen elk voor met kans \(1/4 = 1/2 \times 1/2\). Bijgevolg kan de toevalsveranderlijke \(S\) die de som van de uitkomsten weergeeft, de volgende waarden aannemen:

$$(x_1,x_2)$$ $$s$$ $$P(S=s)$$
(0,0) 0 1/4
(0,1),(1,0) 1 1/2
(1,1) 2 1/4

In het algemeen, als men \(n\) onafhankelijke observaties trekt telkens met kans \(\pi\) op “succes” (uitkomst 1), dan kan het totaal aantal successen \(S\) (of de som van alle 1-en), \(n+1\) mogelijke waarden hebben. Men kan aantonen dat elke waarde \(k\) tussen 0 en \(n\) dan de volgende kans op voorkomen heeft:

\[\begin{equation} P(S=k) = \left ( \begin{array}{c} n \\ k \\ \end{array} \right ) \pi^k (1-\pi)^{n-k} \qquad(5) \end{equation}\]

waarbij \(1-\pi\) de kans is op mislukking in 1 enkele trekking (uitkomst met 0 genoteerd) en \(\left(\begin{array}{c} n \\ k \\ \end{array}\right)\) de binomiaalcoëfficient

\[\begin{equation*} \left ( \begin{array}{c} n \\ k \\ \end{array} \right ) = \frac{n \times (n-1) \times ...\times (n-k+1) }{ k!} = \frac{ n!}{ k!(n-k)! } \end{equation*}\]

is, waarbij \(0!=1!=1\).

In R kan je die kansen opvragen met behulp van het commando dbinom(k,n,p).

Een toevalsveranderlijke \(S\) met een kansverdeling zoals in Model (5) noemt men een Binomiaal verdeelde toevalsveranderlijke. De bijhorende kansverdeling is de Binomiale kansverdeling met parameters \(n\) (d.i. het aantal trekkingen of, equivalent, de maximale uitkomstwaarde) en \(\pi\) (de kans op een `succes’ bij elke trekking). Ze kan gebruikt worden om te berekenen wat de kans is dat er zich op een vast totaal van \(n\) onafhankelijke experimenten \(k\) gebeurtenissen van een bepaald type voordoen, als je weet dat de kans dat zich 1 zo’n gebeurtenis voordoet op 1 experiment, \(\pi\) bedraagt. De Binomiale kansverdeling wordt vooral gebruikt voor de analyse van gegevens die slechts 2 mogelijke waarden kunnen aannemen. Dergelijke gegevens komen vaak voor in wetenschappelijk onderzoek (bijvoorbeeld: al dan niet besmet met HIV, wild type van een gen vs een mutant,…). Kennis van de Binomiale verdeling kan dan helpen om proporties of risico’s op een gebeurtenis van een bepaald type te vergelijken tussen verschillende groepen. Een grafische weergave van enkele Binomiale kansverdelingen is gegeven in Figuur 55.

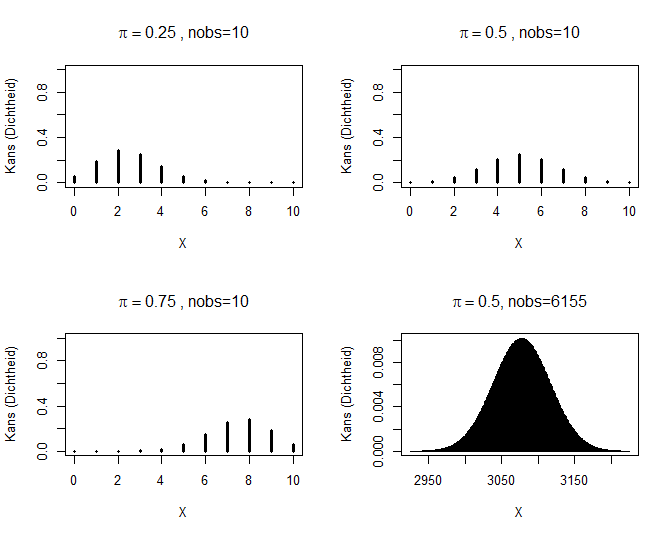
Figuur 55: Binomiale verdelingen.

Om nu te toetsen of \(\pi=1/2\) versus het alternatief dat \(\pi\neq 1/2\), is een voor de hand liggende toetsstatistiek \(\bar X-1/2\) of, equivalent, \(\Delta=n(\bar X-\pi_0)=S-s_0\). De verdeling van deze laatste toetsstatistiek volgt rechtstreeks uit de Binomiale verdeling.

We observeren \(s=\) 3175 en dus \(\delta=s-s_0=\) 3175 \(-\) 6155 \(\times 0.5=\) 97.5. In de onderstelling dat jongens en meisjes even waarschijnlijk zijn (d.i. onder de nulhypothese \(H_0:\pi=1/2\)), kunnen we de bijhorende tweezijdige p-waarde berekenen als de kans dat de uitkomst

\[p=\text{P}_0\left[S-s_0\geq \vert \delta\vert \right] + \text{P}_0\left[S-s_0\leq - \vert \delta\vert \right].\]

Merk op dat we dit kunnen herschrijven in termen van S.

\[p=\text{P}_0\left[S\geq s_0+ \vert \delta\vert \right] + \text{P}_0\left[S \leq s_0 - \vert \delta\vert \right].\]

Voor ons voorbeeld kunnen we deze kansen als volgt berekenen:

\[\begin{eqnarray*} \text{P}_0\left[S\geq s_0+ \vert \delta\vert \right] &=& P(S \geq 6155 \times 0.5 + \vert 3175 - 6155 \times 0.5\vert ) = P(S \geq 3175)\\ &= &P(S= 3175) + P(S=3176) + ... + P(S=6155)\\ & =& 0.0067\\\\ \text{P}_0\left[S \leq s_0 - \vert \delta\vert \right] &=& P(S \leq 6155 \times 0.5 - \vert 3175- 6155 \times 0.5\vert) = P(S \leq 2980)\\ &= &P(S=0) + ... + P(S=2980) \\ &=&0.0067 \end{eqnarray*}\]

Gezien \(\pi=0.5\) zijn deze kansen gelijk omdat de binomiale distributie dan symmetrisch is. Dat is niet langer het geval wanneer \(\pi\) afwijkt van 0.5.

In R kan men de kansen berekenen via de commando’s:

pi0 <- 0.5
s0 <- pi0 *n
delta <- abs(boys- s0)
delta

## [1] 97.5

sUp <- s0 + delta
sDown <- s0 -delta
c(sDown,sUp)

## [1] 2980 3175

#Merk op dat we voor de berekening naar rechts
#pbinom(sUp-1,n,pi) gebruiken omdat we met
#pbinom de kans berekenen in de linkse staart
#anders wordt s=3175 er niet bij geteld!
pUp <- 1 - pbinom(sUp-1, n, pi0)
pUp

## [1] 0.006699883

pDown <- pbinom(sDown, n, pi0)
pDown

## [1] 0.006699883

p <- pUp+pDown
p

## [1] 0.01339977

waarbij pbinom(sUp-1,n,pi0) de kans op een resultaat kleiner of gelijk aan \(s_0+\vert \delta\vert -1 =\) 3174 berekent. Als \(\pi= 1/2\), dan zou de kans om door toeval minstens \(\delta=\) 97.5 jongens meer of minder te observeren dan het gemiddelde onder \(H_0: s_0=\) 3077.5 , slechts 1.34% is, de \(p\)-waarde van de binomiale test.
Dit geeft aan dat het heel onwaarschijnlijk is om een dergelijk groot aantal jongens te observeren als in realiteit jongens en meisjes even waarschijnlijk zijn. Het drukt met andere woorden uit dat de onderstelling dat jongens en meisjes even waarschijnlijk zijn, weinig gesteund wordt door de data. Dit blijkt ook uit Figuur 56.

Figuur 56: Binomiale verdeling van het aantal jongens S onder $$H_0: \pi=0.5 (n=6155)$$.

De test kan eveneens worden uitgevoerd a.d.h.v. de binomial.test functie in R.

binom.test(x = boys, n = n, p = pi0)

## 
## 	Exact binomial test
## 
## data:  boys and n
## number of successes = 3175, number of trials = 6155, p-value = 0.0134
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.5032696 0.5283969
## sample estimates:
## probability of success 
##              0.5158408

Op het 5% significantie-niveau besluiten we dat er gemiddeld meer kans is dat een ongeboren kind mannelijk dan vrouwelijk is.

Voor de Saksen-studie ligt het BI op basis van de CLT heel dicht bij het exacte BI omdat de studie is gebaseerd op een grote steekproef (\(n=\) 6155).

Merk op dat het testen voor een proportie kan gezien worden als het equivalent van een one-sample t-test voor binaire data.

Conclusie

Voor de Saksen populatie besluiten we op het 5% significantieniveau dat er meer kans is dat een ongeboren kind mannelijk dan vrouwelijk is (\(p=\) 0.013). De kans dat een ongeboren kind mannelijk is, bedraagt 51.6% (95% BI \(50.3,52.8\)%).