De Amerikaan Harlan Ellison heeft meer dan 1.700 kortverhalen, novellen, scenario's, stripboeken, essays en een breed scala aan kritieken op literatuur, film, televisie en gedrukte media bij elkaar geschreven. Ondanks het feit dat hij van elke hand slechts één vinger gebruikte om te typen, deed hij dat naar verluidt ook nog eens ontzettend snel.

We vragen ons nu het volgende af: welke woorden waren voor Harlan Ellison het makkelijkst om te typen? Alhoewel deze vraag op verschillende manieren kan gemodelleerd worden, staat vast dat de karakters van de woorden afwisselend met de linker- en de rechterhand moeten getypt worden en dat de afstand in vogelvlucht waarover de vingers zich daarbij verplaatsen zo klein mogelijk moet zijn.
Omdat er geen vaste standaard lijkt te zijn voor de kleine verschuiving tussen de rijen van een toetsenbord, nemen we hier voor de eenvoud aan dat de toetsen op een rechthoekig rooster met eenheidsafstand geplaatst zijn. Een toetsenbord met QWERTY-indeling ziet er dan bijvoorbeeld als volgt uit:
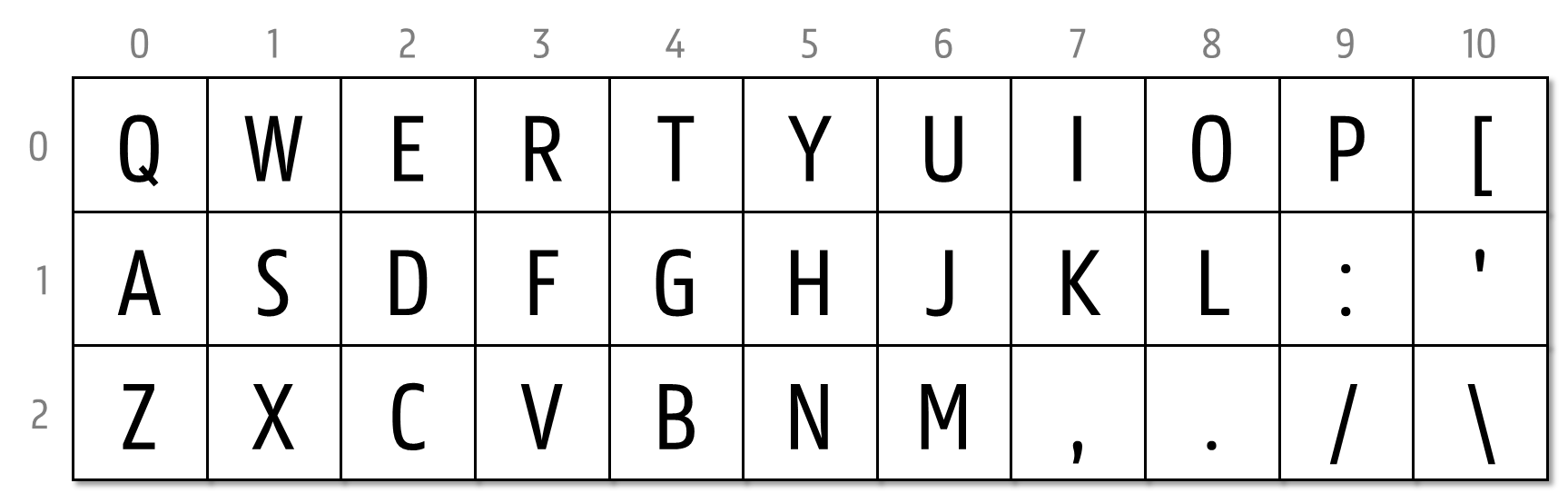
Bij het typen mogen de twee vingers over het hele toetsenbord lopen (zo hoeft bijvoorbeeld de rechterhand dus niet boven de rechterhelft van het toetsenbord te blijven), maar de twee handen mogen elkaar nooit kruisen. We leggen dus de volgende voorwaarde op: elk karakter dat met de rechterhand getypt wordt, staat in een kolom die rechts ligt van de kolom waarin het voorgaande karakter en het volgende karakter staan die met de linkerhand getypt wordt. Het is dus ook niet toegelaten dat twee opeenvolgende karakters op dezelfde kolom staan. Woorden die aan deze voorwaarde voldoen, noemen we Ellisonwoorden.
Als we de rijen van een rechthoekig toetsenbord zoals in bovenstaande afbeelding van boven naar onder nummeren vanaf nul, en de kolommen van links naar rechts, dan kan de positie van elke toets aangeduid worden door een tuple $$(r, k)$$. Daarbij geven $$r$$ en $$k$$ het nummer aan van de rij en de kolom waarop de toets gelegen is. We definiëren de afstand $$d(a_1, a_2)$$ tussen twee toetsen $$a_1$$ en $$a_2$$ op posities $$(r_1, k_1)$$ en $$(r_2, k_2)$$ als \[ d(a_1, a_2) = \sqrt{(r_1 - r_2)^2 + (k_1 - k_2)^2} \] Voor een Ellisonwoord $$w$$ dat bestaat uit de $$n$$ karakters $$a_1a_2\ldots a_n$$ berekenen we de score \[ s(w) = \frac{1}{n-2}\displaystyle\sum_{i=1}^{n-2}d(a_{i}, a_{i+2})\] Deze score is gelijk aan de gemiddelde afstand die de vingers moeten afleggen bij elke verplaatsing naar het volgende karakter dat ze moeten typen. Hoe lager deze score, hoe minder inspanning het vraagt op het woord te typen. Op basis van deze score zijn dit de eenvoudigste Engelstalige Ellisonwoorden van 4 tot en met 13 letters die we gevonden hebben:
| # letters | woorden | score |
|---|---|---|
| 4 | dodo, papa, tutu | 0.00 |
| 5 | dodos, ninon | 0.33 |
| 6 | banana | 0.25 |
| 7 | austere | 1.08 |
| 8 | terebene | 0.71 |
| # letters | woorden | score |
|---|---|---|
| 9 | abatement | 1.44 |
| 10 | maharajas | 1.10 |
| 11 | prohibitory | 1.40 |
| 12 | monotonicity | 1.43 |
| 13 | mononucleus | 1.24 |
Ellison had deze woorden kunnen gebruiken in een verhaal over een uitbraak van besmettelijke ziekten in India, maar men zou dat waarschijnlijk als een teken van luiheid gezien hebben.
Opgave
Een toetsenbordindeling waarbij de toetsen gerangschikt worden op een rechthoekig rooster, stellen we voor als een string (str) waarin elke toets wordt voorgesteld door het karakter dat erop staat. Daarbij worden de toetsen op elke rij van links naar rechts opgelijst, en worden de rijen van boven naar onder opgelijst en van elkaar gescheiden door een verticale streep (|). Hierbij gaan we er dus van uit dat de verticale streep zelf niet voorkomt als karakter op een toets. Voorts moet een geldige toetsenbordindeling aan de volgende voorwaarden voldoen:
-
alle rijen bevatten evenveel toetsen
-
hetzelfde karakter komt nooit voor op twee verschillende toetsen (hierbij maken we geen onderscheid tussen hoofdletters en kleine letters)
Gevraagd wordt:
-
Schrijf een functie is_toetsenbord waaraan een toetsenbordindeling (str) moet doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of de gegeven toetsenbordindeling geldig is.
-
Schrijf een functie vingerpositie waaraan een karakter $$c$$ (str) moet doorgegeven worden. Als $$c$$ niet voorkomt op het toetsenbord, dan moet een AssertionError opgeworpen worden met de boodschap onbekend karakter. Anders moet de positie van toets $$c$$ teruggegeven worden.
-
Schrijf een functie vingerposities waaraan een woord $$w$$ (str) moet doorgegeven worden. De functie moet een lijst (list) teruggeven met de posities van de opeenvolgende karakters in $$w$$.
-
Schrijf een functie verplaatsingen waaraan een woord $$w$$ (str) moet doorgegeven worden. De functie moet een string (str) teruggeven waarvan de letters corresponderen met de kolomverplaatsingen tussen de opeenvolgende karakters van $$w$$: R als het volgende karakter in een kolom naar rechts staat, L als het volgende karakter in een kolom naar links staat en S als het volgende karakter in dezelfde kolom staat.
-
Schrijf een functie is_ellisonwoord waaraan een woord $$w$$ (str) moet doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of $$w$$ een Ellisonwoord is.
-
Schrijf een functie score waaraan een woord $$w$$ (str) moet doorgegeven worden. Als $$w$$ geen Ellisonwoord is dan moet de functie een AssertionError opwerpen met de boodschap geen Ellisonwoord. Anders moet de functie de score $$s(w)$$ teruggeven.
Deze functies mogen geen onderscheid maken tussen hoofdletters en kleine letters. Behalve de functie is_toetsenbord hebben alle andere functies ook nog een optionele parameter toetsenbord waaraan een toetsenbordindeling (str) kan doorgegeven worden die de posities van de toetsen op het toetsenbord vastlegt. De functies gebruiken de QWERTY-toetsenbordindeling uit de inleiding als er niet expliciet een argument wordt doorgegeven aan de parameter toetsenbord. Als het gegeven toetsenbord niet geldig is dan moet een AssertionError opgeworpen worden met de boodschap ongeldig toetsenbord.
Voorbeeld
>>> QWERTY = "QWERTYUIOP[|ASDFGHJKL:'|ZXCVBNM,.\\/"
>>> AZERTY = 'AZERTYUIOP^|QSDFGHJKLM%|WXCVBN?./+='
>>> is_toetsenbord(QWERTY)
True
>>> is_toetsenbord(AZERTY)
True
>>> is_toetsenbord(42)
False
>>> is_toetsenbord('ABC|DEF|ABC')
False
>>> is_toetsenbord('ABC|DEF|GHIJ')
False
>>> vingerpositie('W')
(0, 1)
>>> vingerpositie('w', toetsenbord=AZERTY)
(2, 0)
>>> vingerpositie('ß')
Traceback (most recent call last):
AssertionError: onbekend karakter
>>> vingerposities('abatement')
[(1, 0), (2, 4), (1, 0), (0, 4), (0, 2), (2, 6), (0, 2), (2, 5), (0, 4)]
>>> vingerposities('monotonicity')
[(2, 6), (0, 8), (2, 5), (0, 8), (0, 4), (0, 8), (2, 5), (0, 7), (2, 2), (0, 7), (0, 4), (0, 5)]
>>> vingerposities('monotonicity', toetsenbord=AZERTY)
[(1, 9), (0, 8), (2, 5), (0, 8), (0, 4), (0, 8), (2, 5), (0, 7), (2, 2), (0, 7), (0, 4), (0, 5)]
>>> vingerposities('Ellison')
[(0, 2), (1, 8), (1, 8), (0, 7), (1, 1), (0, 8), (2, 5)]
>>> verplaatsingen('abatement')
'RLRLRLRL'
>>> verplaatsingen('monotonicity')
'RLRLRLRLRLR'
>>> verplaatsingen('monotonicity', toetsenbord=AZERTY)
'LLRLRLRLRLR'
>>> verplaatsingen('Ellison')
'RSLLRL'
>>> is_ellisonwoord('abatement')
True
>>> is_ellisonwoord('monotonicity')
True
>>> is_ellisonwoord('monotonicity', toetsenbord=AZERTY)
False
>>> is_ellisonwoord('Ellison')
False
>>> score('dodo')
0.0
>>> score('dodos')
0.3333333333333333
>>> score('banana')
0.25
>>> score('austere')
1.082842712474619
>>> score('terebene')
0.7060113295832983
>>> score('abatement')
1.4377850146065685
>>> score('maharajahs')
1.101569900005158
>>> score('prohibitory', toetsenbord=AZERTY)
1.405586837763654
>>> score('monotonicity')
1.430056307974577
>>> score('mononucleosis')
1.2409346854429897