Een kleuring van een graaf \(G\) is een toekenning van kleuren (elementen van een bepaalde verzameling) aan de toppen van \(G\), één kleur per top, zodanig dat adjacente toppen een verschillende kleur krijgen. Wanneer \(k\) kleuren worden gebruikt, wordt dit een \(k\)-kleuring genoemd. Indien er een \(k\)-kleuring voor een graaf \(G\) bestaat, dan noemt men de graaf \(G\) \(k\)-kleurbaar.

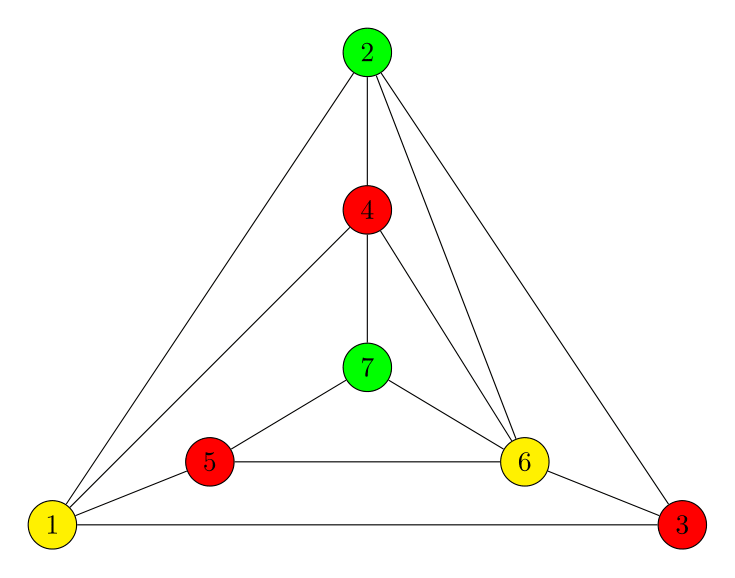
Gegeven is de graaf in bovenstaande afbeelding. Deze graaf is 3-kleurbaar, de kleuren van de toppen zijn weergegeven in de figuur. Merk op dat er geen twee adjacente toppen zijn die dezelfde kleur hebben.

Opgave

Schrijf een Python-functie kleuring_mogelijk(graph, aantal_kleuren) die een graaf \(G\) en het aantal te gebruiken kleuren \(k\) als parameters mee krijgt. Deze functie moet True teruggeven als het mogelijk is om \(G\) te kleuren met \(k\) kleuren, en anders False.

We maken bij deze oefening gebruik van een eenvoudige grafenbibliotheek graphlib. De API van de deze bibliotheek vind je hier¹. Neem eerst en vooral eens de API en de bibliotheek zelf door en stel eventueel vragen hierover voor je begint te programmeren.

Belangrijke opmerking: om met de grafenbibliotheek te kunnen werken in PyCharm moet je het bestand graph_library.py² toevoegen aan dezelfde directory als waarin je ze gebruikt. Dan kun je ze gebruiken door ze te importeren met

from graph_library import *

Dit import statement mag wel niet mee ingediend worden op dodona.

Voorbeelden

>>> graph = undirected_graph_from_dict({'Alice': ['Bob', 'Carol'], 'Bob': ['Alice', 'Carol', 'Dan'], 'Carol': ['Alice', 'Dan', 'Bob'], 'Dan': ['Bob', 'Carol']})
>>> kleuring_mogelijk(graph, 2)
False
>>> kleuring_mogelijk(graph, 3)
True