Een koppelbureau wil $$n$$ mannen $$m_0, m_1, \ldots, m_{n-1}$$ koppelen aan $$n$$ vrouwen $$v_0, v_1, \ldots, v_{n-1}$$. Aan elke man en elke vrouw werd gevraagd om alle kandidaten van het andere geslacht te rangschikken naar persoonlijke voorkeur. Deze voorkeuren van de mannen en de vrouwen kunnen voorgesteld worden in twee $$n \times n$$ tabellen. Hierbij geeft de eerste rij van de tabel met de voorkeur van de mannen bijvoorbeeld de rangschikking van man $$m_0$$ aan, waarbij een waarde $$i$$ ($$0 \leq i < n$$) in de eerste kolom aangeeft dat de eerste keuze van man $$m_0$$ uitgaat naar vrouw $$v_i$$. Een waarde $$j$$ ($$0 \leq j < n$$) in de tweede kolom geeft analoog aan dat de tweede keuze van man $$m_0$$ uitgaat naar vrouw $$v_j$$. Op dezelfde manier geeft de tweede rij de rangschikking van de vrouwen zoals die werd opgesteld door man $$m_1$$. De tabel met de voorkeur van de vrouwen is op dezelfde manier opgebouwd.
Hieronder staan bijvoorbeeld de tabellen met de voorkeuren voor 4 mannen en 4 vrouwen, waarbij de kandidaten van beide groepen gelabeld worden met de getallen 0, 1, 2, en 3.
| voorkeur mannen | ||||
|---|---|---|---|---|
| 0 | 1 | 0 | 2 | 3 |
| 1 | 3 | 0 | 1 | 2 |
| 2 | 0 | 2 | 1 | 3 |
| 3 | 1 | 2 | 0 | 3 |
| voorkeur vrouwen | ||||
|---|---|---|---|---|
| 0 | 0 | 2 | 1 | 3 |
| 1 | 2 | 3 | 0 | 1 |
| 2 | 3 | 1 | 2 | 0 |
| 3 | 2 | 1 | 0 | 3 |
Uit voorgaande tabellen leiden we bijvoorbeeld af dat de eerste keuze van man $$m_0$$ uitgaat naar vrouw $$v_1$$, terwijl man $$m_0$$ zelf slechts de derde keuze is van vrouw $$v_1$$.
Rekening houdend met de persoonlijke voorkeuren wil het koppelbureau de mannen en de vrouwen paarsgewijs aan elkaar koppelen. Ze willen dit echter op zo'n manier doen dat geen enkele man en geen enkele vrouw liever elkaar zouden hebben dan de partner waaraan ze gekoppeld werden. Indien dit lukt, dan is de kans immers zeer groot dat dit zal leiden tot stabiele huwelijken. Voor een zeer welsprekende uiteenzetting van het stable marriage problem en bijkomende achtergrondinformatie verwijzen we naar dit artikel.
Algoritme
In 1962 bewezen David Gale en Lloyd Shapley dat het voor een gelijk aantal mannen en vrouwen altijd mogelijk is om een stabiele oplossing te vinden voor het bovenstaande probleem. Ze gaven daarbij ook een algoritme om de oplossing te vinden. Dit Gale-Shapley algoritme kan als volgt omschreven worden:
initieel zijn alle mannen en vrouwen nog vrij (niet gekoppeld)
zolang er nog een man m is die niet aan een vrouw gekoppeld is
zoek eerst gerangschikte vrouw v die man m nog niet heeft aangezocht (*)
als vrouw v nog niet gekoppeld is aan een man
koppel dan man m aan vrouw v
anders is vrouw v reeds gekoppeld aan mannelijke concurrent c
als vrouw v man m verkiest boven man c
koppel dan man m aan vrouw v
man c is terug een vrij man
anders blijft vrouw v aan man c gekoppeld Gale en Shapley toonden ook aan dat er op punt (*) van het algoritme gegarandeerd steeds een vrouw $$v$$ is waaraan de vrije man $$m$$ nog geen aanzoek gedaan heeft.
Voor de bovenstaande voorkeurstabellen doorloopt het algoritme de volgende stappen:
-
iteratie 1: man 0 kiest vrouw 1 (zijn eerste keuze)
-
iteratie 2: man 1 kiest vrouw 3 (zijn eerste keuze)
-
iteratie 3: man 2 kiest vrouw 0 (zijn eerste keuze)
-
iteratie 4: man 3 kiest vrouw 1 (zijn eerste keuze), want vrouw 1 verkiest man 3 boven man 0; man 0 is terug vrij
-
iteratie 5: man 0 kiest vrouw 0 (zijn tweede keuze), want vrouw 0 verkiest man 0 boven man 2; man 2 is terug vrij
-
iteratie 6: man 2 kiest vrouw 2 (zijn tweede keuze)
-
alle vrouwen zijn nu aan mannen gekoppeld
-
man 0 $$\rightarrow$$ vrouw 0
-
man 1 $$\rightarrow$$ vrouw 3
-
man 2 $$\rightarrow$$ vrouw 2
-
man 3 $$\rightarrow$$ vrouw 1
-
Opgave
Implementeer de interface DatingService in een klasse genaamd StableDatingService.
Hiervoor schrijf je een functie public int[] match(int[][] men, int[][] women) die, gegeven respectievelijk de $$n \times n$$
tabel met voorkeuren van de mannen en van de vrouwen, stabiele koppels vormt volgens het Gale-Shapley algoritme.
Als resultaat geef je een array terug met als i-de element het identificatienummer van de vrouw die aan de i-de man gekoppeld werd.
In het hierboven beschreven voorbeeld is de uitvoer de array [0, 3, 2, 1]. De oplossing voor dit voorbeeld
wordt hieronder grafisch weergegeven.
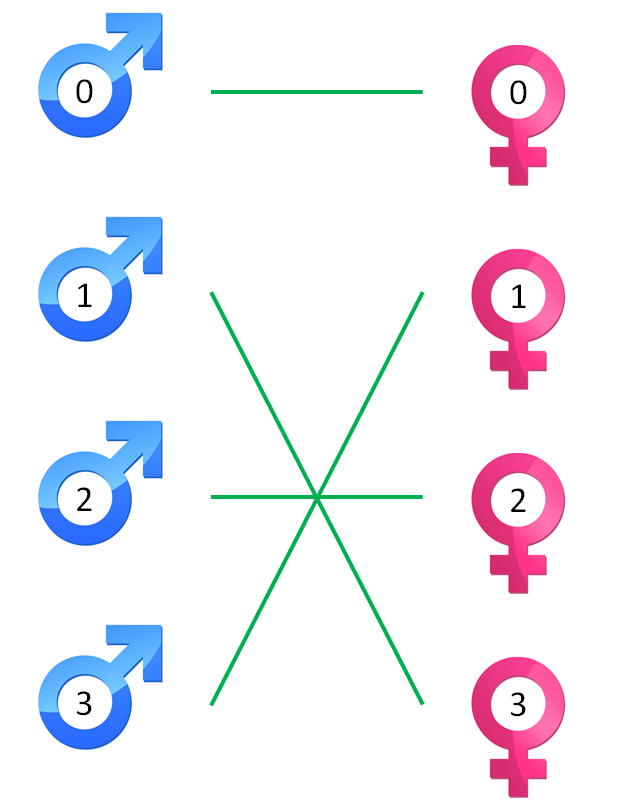
Gebruik eventueel de testklasse SimpleTest om je oplossing lokaal te testen. Je kan hierin eenvoudig extra testgevallen toevoegen.