Een aantal munten liggen verspreid over de cellen van een \(n\times m\)-rooster, waarbij elke cel hoogstens 1 munt bevat, zoals getoond in bijgaande figuur.

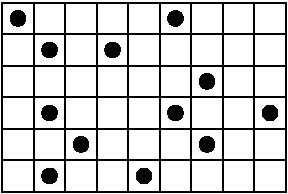
Een robot start in de cel links boven van het rooster en verplaatst zich naar de cel rechts onder van het rooster. In elke stap kan de robot zich ofwel naar de cel rechts van zijn huidige locatie verplaatsen, ofwel naar de cel onder zijn huidige locatie. Wanneer de robot een cel met een munt bezoekt, dan neemt hij die munt mee. Het is de bedoeling dat de robot zoveel mogelijk munten verzamelt.

Ontwerp en implementeer een algoritme dat bepaalt wat het maximum aantal munten is dat de robot kan verzamelen, evenals een pad dat de robot moet hiervoor moet volgen.

Opgave

Schrijf een Python-functie verzamel(matrix: list) die een matrix van nullen en enen binnenkrijgt en een pad teruggeeft dat op de linkerbovenhoek start en in de rechteronderhoek eindigt. Dat pad moet als string teruggegeven worden, bestaande uit de karakters \(→\) en \(↓\). (Indien deze nog niet op je toetsenbord staan kun je deze gewoon uit de opgave kopieren).

Voorbeeld

>>> verzamel([[0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 1, 0], [0, 0, 0, 1, 0, 1], [1, 1, 0, 0, 0, 1], [0, 1, 0, 0, 1, 0], [0, 0, 0, 1, 1, 0]])
"→→↓→→→↓↓↓↓"