Geschiedenis

Darts (of darten) is een eeuwenoud spel dat zou ontstaan zijn toen soldaten wedstrijden begonnen te houden als tijdverdrijf tussen veldslagen door. Daarbij werden korte speren gegooid op omgekeerde bodems van wijntonnen en later op doorgezaagde boomstamschijven. Op de schijven werd een puntentelling aangebracht. In de wintermaanden werd de sport noodgedwongen binnen gehouden, wat tot gevolg had dat men de kleine speren moest vervangen door darts en er een nieuwe regelgeving voor het beoefenen van de binnensport werd bedacht. Naarmate het spel zich verder ontwikkelde, begonnen de rijkere lagen van de bevolking ook interesse te tonen in darts. Zo staat er geschreven dat Hendrik VIII in 1530 van zijn tweede vrouw Anne Boleyn een kostbaar versierde Biscayan-dartset geschonken kreeg.

Een oude Nederlandse en in de Vlaamse spreektaal nog gebruikelijke naam van het spel is vogelpik. Deze term is afkomstig van een soortgelijk spel dat vroeger gespeeld werd in cafés. Dit spel bestond uit een roos met ringen, niet zoals het actueel dartbord dus, en een nagemaakte vogel met een scherpe snavel. De vogel werd met een koord aan het plafond opgehangen en de spelers probeerden de snavel van de vogel in de roos te zwieren.

Dartbord

Het wedstrijdbord dat tegenwoordig gebruikt wordt, komt uit Londen. Het bord bestaat uit een ronde vezelplaat van 18 millimeter dik, waarop sisalvezelborsteltjes onder grote druk gelijmd en geperst worden. Het geheel wordt omlijst door een metalen band. Het bord wordt voorzien van een vakindeling door middel van verschillende kleuren. Vervolgens wordt er een metalen web op bevestigd dat diezelfde vakindeling heeft. De functie van dit web is ervoor te zorgen dat altijd duidelijk is in welk vak een dart gegooid is. Op de buitenzijde wordt een metalen ring aangebracht waarop volgens de vakindeling bepaalde cijfers zijn bevestigd. Deze ring is los te maken, zodat de cijfers ten opzichte van het bord verschoven kunnen worden.

Het is de bedoeling dat het vak (bed) 20 middenboven zit. Op deze 20 wordt normaal gesproken het meest gegooid. Hierdoor zal de bodemplaat in dit vak dan ook het eerste kapot gaan. Elke dart die gegooid wordt tast immers de vezeltjes van het bord aan. Door de lijmlaag valt het bord niet uit elkaar, maar na verloop van tijd wordt op bepaalde plaatsen een opeenhoping van vezeltjes zichtbaar, in de vorm van bulten. Om dit te voorkomen, dient het bord om de zoveel tijd gedraaid te worden, zodat het cijfer twintig weer boven een nieuw, minder gehavend deel van het bord staat. De 20 staat wel altijd boven een zwart deel. Moderne sisalvezelborden moeten beslist niet worden natgemaakt zoals nog wel eens wordt gedacht.

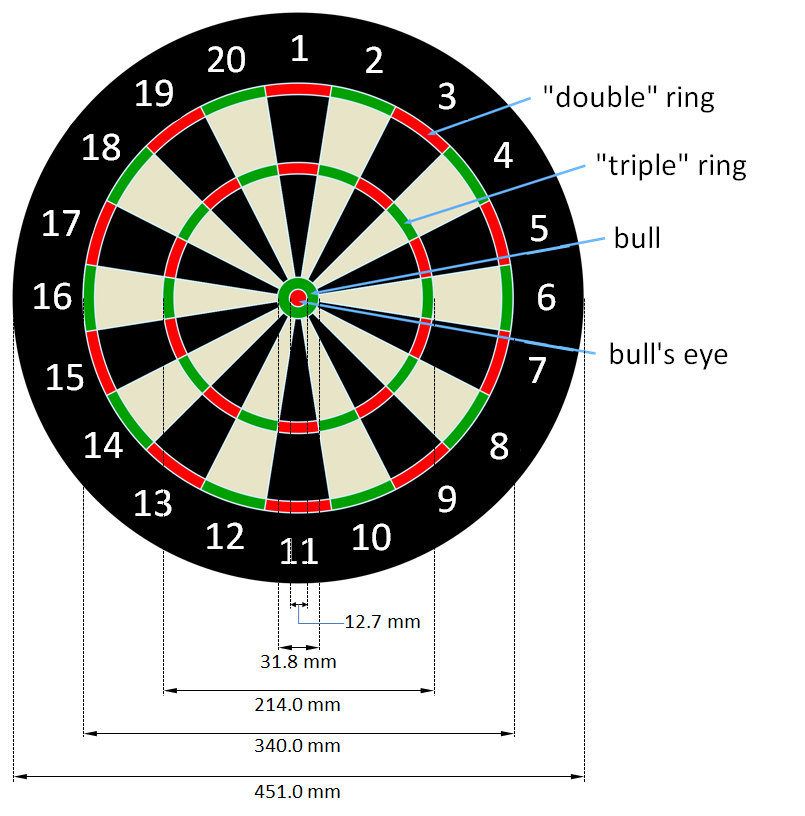
De afmetingen van het dartbord worden aangegeven in bovenstaande figuur. De double ring en triple ring zijn telkens 9.6 mm breed.

Puntentelling

Het dartbord is verdeeld in ringen en sectoren. De getallen langs de rand geven het aantal punten aan voor een pijltje in de desbetreffende sector. Voor deze opgave zijn de sectoren in wijzerzin genummerd vanaf 1 en dit vanaf de bovenste sector. De sectoren zijn onderverdeeld in nog een aantal kleinere vakken.

• in het midden is de double bull of bull's eye (rood), 50 punten

• daaromheen de single bull (groen), 25 punten

• daaromheen een brede ring, het bed (zwart en wit), waarvoor het aantal punten geldt dat op de rand van het bord staat

• daaromheen een smalle ring, de triple (of treble) ring (rood en groen); deze levert drie maal het puntenaantal op

• daaromheen weer een bed

• daaromheen de double ring (rood en groen) met twee keer het aantal punten dat bij het betreffende vak staat

Een dart in de buitenste zwarte rand (waar de cijfers staan) of naast het bord levert geen punten op. Een bouncer — een dart die van het bord terugkaatst — heeft ook geen score tot gevolg. Daarnaast is er ook geen score wanneer een dart na geworpen te zijn plots uit het bord valt voordat de speler in de gelegenheid was alle drie zijn pijlen uit het bord te halen (let wel, dit wordt officieel geen bouncer genoemd). Als een speler een dart in één van zijn eerder gegooide darts gooit (een Robin Hood), wordt de laatste van die twee darts wel gezien als zijnde 'geworpen', maar wordt er geen score aan die dart toegekend.

Opgave

We beschouwen een carthesisch coördinatenstelsel¹ met oorsprong in het centrum van de bull's eye van een dartboard. Een speler werpt een pijltje naar het dartbord dat belandt op de coördinaten $$(x, y)$$, waarbij beide coördinaten worden uitgedrukt in millimeter. Bepaal het aantal punten dat met dit pijltje behaald wordt. Hiervoor kan je best eerst de carthesische coördinaten $$(x, y)$$ van de positie waar het pijltje belandt omzetten naar poolcoördinaten $$(r, \theta)$$, om daarna op basis van de hoek $$\theta$$ de score van de corresponderende sector te bepalen.

Van carthesische coördinaten naar poolcoördinaten

De eerste stap naar de oplossing bestaat erin de positie $$P$$ waar het pijltje beland is op het dartbord om zetten van coördinaten $$(x, y)$$ in het carthesisch coördinatenstelsel naar poolcoördinaten² $$(r, \theta)$$. Het koppel reële getallen $$(r, \theta)$$ drukt dus de positie van het punt $$P$$ uit in poolcoördinaten, waarbij de pool $$O$$ samenvalt met het centrum van de bull's eye, en de poolas samenvalt met de $$X$$-as. De coördinaat $$r$$ van het punt $$P$$ is de afstand $$OP$$. De coördinaat $$\theta$$ geeft de georiënteerde hoek aan tussen de positieve $$X$$-as en de halfrechte van O door P. Deze hoek wordt uitgedrukt in radialen, en er moet gelden dat $$-\pi < \theta \leq \pi$$.

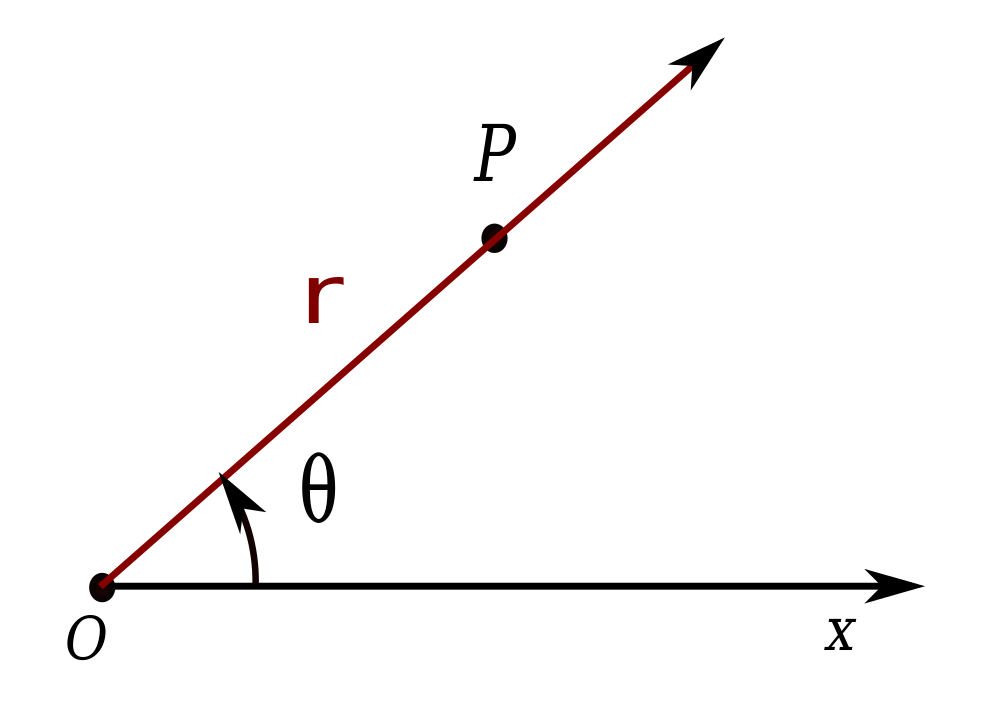
Het verband tussen de carthesische coördinaten $$(x, y)$$ en de poolcoördinaten $$(r, \theta)$$ wordt dan gegeven door \[\begin{cases} r = & \sqrt{x^2+y^2} \\ \\ \theta = & \arctan\left(\frac{y}{x}\right) \end{cases}\]

Van hoek naar sector

Onderstaande schets maakt duidelijk hoe je een hoek in poolcoördinaten ($$\theta$$; de groene hoek) kunt omzetten naar een hoek ($$\beta$$; de rode hoek) die je kunt gebruiken om de index van de overeenkomstige sector te bepalen, en dus ook rechtstreeks de score (die een eenheid hoger is dan de index van de sector).

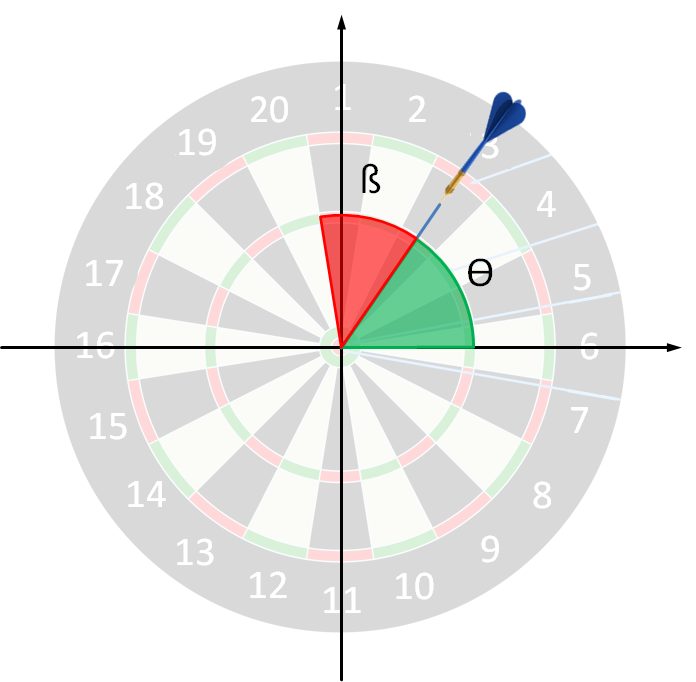
Met een beetje goniometrie is het makkelijk in te zien dat \[ \beta + \theta = \frac{\pi}{2} + \frac{\pi}{20}\,, \] met andere woorden \[ \beta = \frac{\pi}{2} + \frac{\pi}{20} - \theta\,. \] Als je eenmaal $$\beta$$ bepaald hebt, en je weet dat elke sector een hoek van $$\frac{\pi}{10}$$ beslaat, dan kan je de hoek $$\beta$$ omzetten naar de index van de sector. De eerste sector (deze bovenaan de $$Y$$-as) heeft dan index 0, die rechts ervan index 1, enzoverder in wijzerzin.

Invoer

Twee getallen $$x, y \in \mathbb{R}$$, elk op een afzonderlijke regel. Deze getallen stellen de positie $$(x, y)$$ voor van een punt $$P$$ in het carthesisch coördinatenstelsel met oorsprong in het centrum van de bull's eye van een dartboard. De eenheden van het coördinatenstelsel zijn uitgedrukt in millimeter.

Uitvoer

De score die behaald wordt met een pijltje dat gegooid wordt in punt $$P$$ op het dartbord.

Voorbeeld

Invoer:

-30.0
22.0

Uitvoer:

18