In 1917 vroeg Henry Dudeney zich af hoeveel punten er maximaal op een $$n \times n$$ rooster kunnen geplaatst worden als er geen drie verschillende punten op dezelfde rechte mogen liggen. Het is duidelijk dat het antwoord nooit groter kan zijn dan $$2n$$. Als er meer dan $$2n$$ punten op een $$n \times n$$ rooster geplaatst worden, dan volgt immers uit het duivenhokprincipe1 dat er minstens drie punten op dezelfde rij of dezelfde kolom moeten liggen.
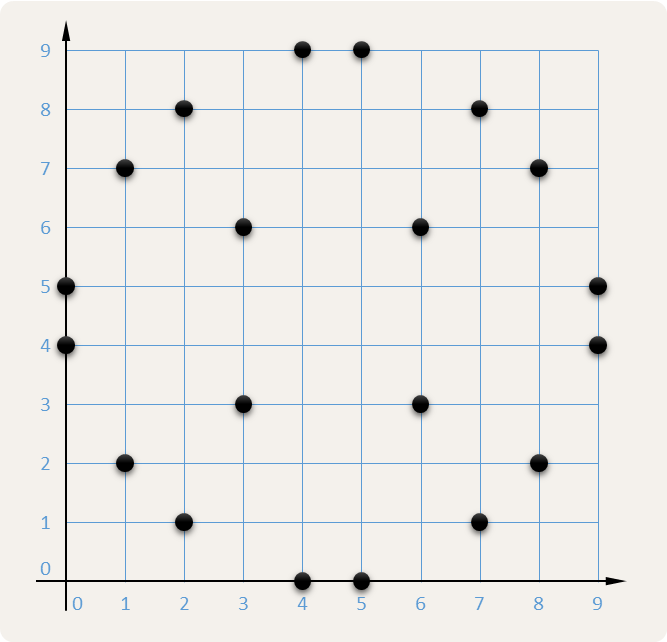
Voor $$n = 10$$ geeft bovenstaande rooster aan dat het mogelijk is om $$2n = 20$$ punten te plaatsen zonder dat er drie verschillende punten op dezelfde rechte liggen. Er werden al oplossingen gevonden om $$2n$$ punten te plaatsen voor elke vierkant rooster tot en met $$n = 52$$. Voor grotere roosters bestaat het vermoeden dat het niet altijd mogelijk is om $$2n$$ punten te plaatsen zonder dat er drie punten op dezelfde rechte liggen, maar op vandaag — meer dan een eeuw nadat Dudeney de vraag stelde — moet het definitieve antwoord nog altijd gevonden worden.
Opgave
Beschouw een $$n \times n$$ rooster voor een gegeven $$n \in \mathbb{N}_0$$. Een punt in het rooster wordt voorgesteld door een tuple $$(x, y)$$ waarbij $$x, y \in \mathbb{N}$$ (int) en $$0 \leq x, y < n$$.
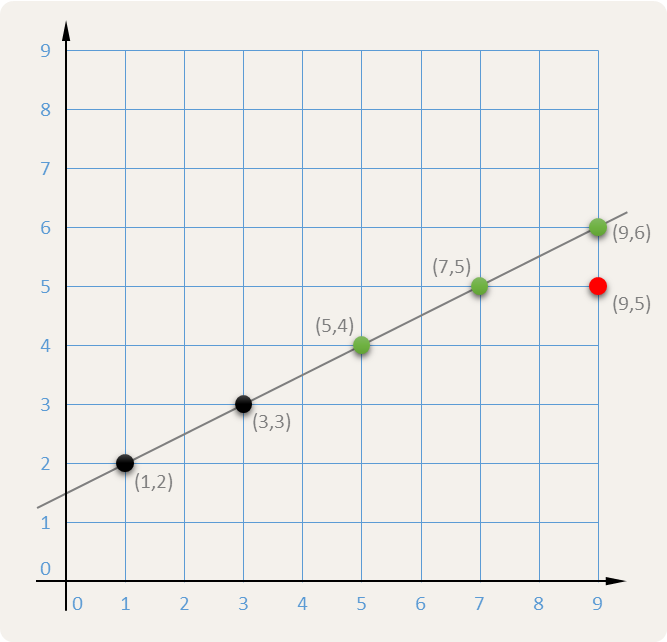
We zeggen dat drie punten $$(x_1, y_1)$$, $$(x_2, y_2)$$ en $$(x_3, y_3)$$ collineair zijn als ze op dezelfde rechte gelegen zijn. Dat is het geval als \[ (x_1 - x_2)(y_1 - y_3) = (x_1 - x_3)(y_1 - y_2) \] Deze formule werkt ook als er twee of drie punten gelijk zijn, want in die gevallen zijn de drie punten altijd collineair. Elk van de drie groene punten in onderstaand rooster is collineair met de twee zwarte punten. Het rode punt is niet collineair met de twee zwarte punten.
Gevraagd wordt:
-
Schrijf een functie zijn_collineair waaraan drie punten $$p_1$$, $$p_2$$ en $$p_3$$ moeten doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of $$p_1$$, $$p_2$$ en $$p_3$$ collineair zijn.
-
Schrijf een functie collineaire_punten waaraan drie argumenten moeten doorgegeven worden: een getal $$n \in \mathbb{N}_0$$ (int) en twee punten $$p_1$$ en $$p_2$$. De functie moet de verzameling (set) met alle punten van een $$n \times n$$ rooster teruggeven die collineair zijn met $$p_1$$ en $$p_2$$.
-
Schrijf een functie geen_drie_op_een_rij waaraan een collectie (list, tuple of set) met punten moet doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of er geen drie verschillende punten in de gegeven collectie collineair zijn.
-
Schrijf een functie niet_collineaire_punten waaraan twee argumenten moeten doorgegeven worden: een getal $$n \in \mathbb{N}_0$$ (int) en een collectie (list, tuple of set) met punten. De functie moet de verzameling (set) met alle punten van een $$n \times n$$ rooster teruggeven die niet collineair zijn met elk paar verschillende punten uit de gegeven collectie.
Voorbeeld
>>> zijn_collineair((1, 2), (3, 3), (7, 5))
True
>>> zijn_collineair((1, 2), (3, 3), (9, 4))
False
>>> collineaire_punten(10, (1, 2), (3, 3))
{(1, 2), (3, 3), (5, 4), (7, 5), (9, 6)}
>>> collineaire_punten(10, (2, 2), (8, 8))
{(0, 0), (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (7, 7), (8, 8), (9, 9)}
>>> punten = [(0, 4), (0, 5), (1, 2), (1, 7), (2, 1), (2, 8), (3, 3), (3, 6), (4, 0), (4, 9), (5, 0), (5, 9), (6, 3), (6, 6), (7, 1), (7, 8), (8, 2), (8, 7), (9, 4), (9, 5)]
>>> geen_drie_op_een_rij(punten)
True
>>> niet_collineaire_punten(10, punten)
set()
>>> punten = {(0, 4), (1, 2), (1, 7), (2, 8), (3, 6), (4, 9), (5, 0), (6, 3), (7, 1), (7, 8), (8, 2), (8, 7), (9, 5)}
>>> niet_collineaire_punten(10, punten)
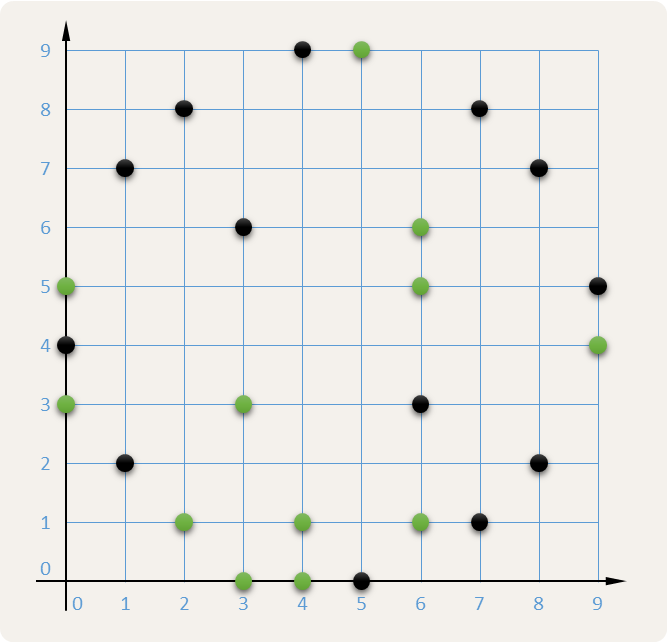
{(4, 0), (2, 1), (9, 4), (4, 1), (0, 5), (6, 1), (3, 0), (6, 5), (5, 9), (6, 6), (0, 3), (3, 3)}De punten die in het groen aangeduid worden in onderstaand rooster zijn alle punten die niet collineair zijn met elk paar zwarte punten. Ze corresponderen met de verzameling die wordt teruggegeven door de laatste functie-aanroep uit het voorbeeld.