Nagaan van modelveronderstellingen

Voor de statistische besluitvorming hebben we volgende aannames gedaan

1. Lineariteit
2. Onafhankelijkheid
3. Homoscedasticiteit
4. Normaliteit

Onafhankelijkheid is moeilijk te verifiëren op basis van de data, dat zou gegarandeerd moeten zijn door het design van de studie. Als we afwijkingen zien van lineariteit dan heeft besluitvorming geen zin gezien het de primaire veronderstelling is. In dat geval moeten we het conditioneel gemiddelde eerst beter modelleren. In geval van lineariteit maar schendingen van homoscedasticiteit of normaliteit dan weten we dat de besluitvorming mogelijks incorrect is omdat de teststatistieken dan niet langer een t-verdeling volgen.

Lineariteit

De primaire veronderstelling in meervoudige lineaire regressie-analyse is de aanname dat de uitkomst (afhankelijke variabele) lineair varieert in functie van de verklarende variabelen.

Afwijkingen van lineariteit kunnen opnieuw worden opgespoord d.m.v. een residuplot. Deze wordt weergegeven in Figuur 62 links boven. Als de veronderstelling van lineariteit opgaat, krijgt men in een residuplot geen patroon te zien. De residuen zijn immers gemiddeld nul voor elke waarde van de predictoren en zouden dus mooi rond nul moeten variëren. Dat is inderdaad het geval voor het meervoudig lineaire regressiemodel dat we hebben gefit o.b.v. de prostaat dataset.

par(mfrow=c(2,2))
plot(lmVWS)

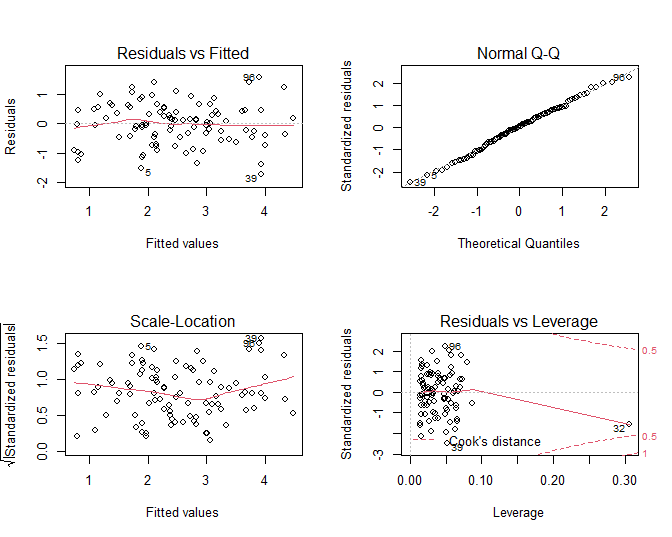
Figuur 62: Diagnostische plots voor het nagaan van de veronderstellingen van het lineair regressiemodel waarbij lpsa gemodelleerd wordt a.d.h.v. de predictoren lcavol, lweight en svi.

Homoscedasticiteit

De residu-plot kan opnieuw worden gebruikt om de veronderstelling na te gaan van homoscedasticiteit of gelijkheid van variantie. De residu-plot voor het prostaatkanker voorbeeld Figuur 62 links boven geeft geen afwijkingen weer van homoscedasiticiteit. Alle residuen zijn mooi gespreid binnen dezelfde grenzen voor elke gefitte waarde \(\hat y_i\). De plot van de vierkantswortel van de absolute waarde van de gestandardiseerde error \(\sqrt{|e_i|/\sqrt{MSE}}\) in functie van de predicties (Figuur 62 links onder) geeft ook geen afwijkingen van homoscedasticiteit weer.

Normaliteit

Opnieuw kunnen we de veronderstelling van normaliteit nagaan door gebruik te maken van QQ-plots. Figuur 62 rechts boven geeft de QQ-plot weer van de residuen voor het prostaatkanker voorbeeld. We zien in de plot geen aanwijzing voor afwijkingen van normaliteit.