Toets voor associatie tussen 2 kwalitatieve variabelen
Gepaarde gegevens
Net zoals bij het vergelijken van gemiddelden (uitkomsten op 2 continue veranderlijken) is het ook hier in principe mogelijk dezelfde individuen 2 keer te meten (bijvoorbeeld, vóór en na blootstelling aan de experimentele stof) en telkens de uitkomst te observeren. In dat geval hebben we te maken met gepaarde binaire uitkomsten en moeten we in de statistische analyse rekening houden met de paring.
Voorbeeld
Rogovin et al. (2017) onderzochten de partnerkeuze van seksueel mature vrouwelijke Campbelli dwerghamster. Hiervoor bekeken ze verschillende karakteristieken van de mannetjes, waaronder seksgerelateerde morfologische kenmerken (lichaamsmassa, externe testikel diameter), testosteron niveau, immunocompetentie kenmerken (de concentratie aan T-cel en B-cel immuuncellen in het bloed), maar ook gedragskenmerken zoals agressiviteit en seksuele dominantie van het mannetje.
De experimentele set-up betreft een rechthoekige doos van plexiglas met drie compartimenten, waarin het vrouwtje zich in het middenste gedeelte bevindt (zie Figuur 57).
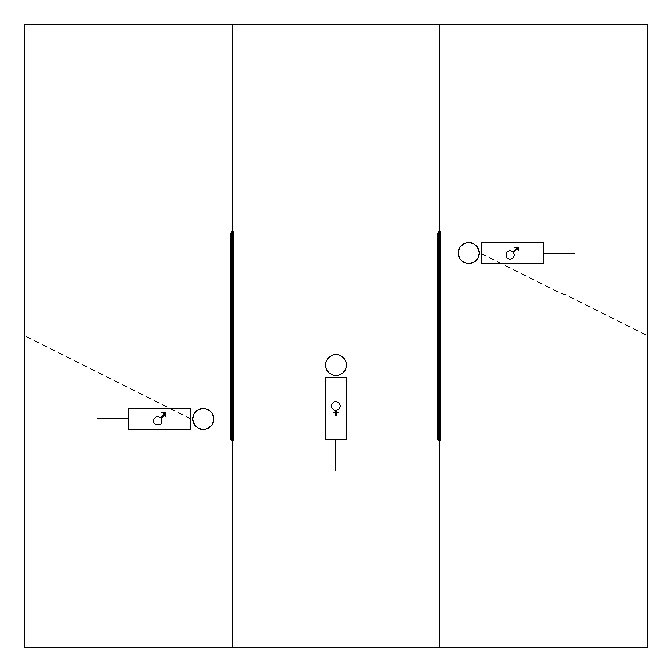
Figuur 57: Experimentele opstelling voor het bepalen van de partnerkeuze bij dwerghamsters
De mannetjes, die overigens broers zijn, hangen vast aan de doos waardoor ze zich slechts over drie vierden van de ruimte van hun compartiment vrij kunnen bewegen. Na alle dieren enkele minuten te laten acclimatiseren worden niet-doorzichtige wanden die de compartimenten scheidden, opgetrokken waardoor het vrouwtje zich via de aangegeven deurtjes naar de mannetjes kan begeven. Aangezien de mannetjes zich niet buiten hun compartiment kunnen begeven, ligt de keuze volledig in de handen van het vrouwtje. Het wordt aangenomen dat het vrouwtje een partnerkeuze maakt indien ze meer dan twee derden van de tijd met één mannetje doorbrengt, relatief ten opzichte van de totale tijd die ze met mannetjes doorbrengt.
Elk vrouwtje onderging tweemaal de test, waarbij ze telkens kon kiezen tussen één agressief en één niet-agressief mannetje. Om te onderzoeken of de partnerkeuze van het vrouwtje beïnvloed wordt door de omgeving, kwam het vrouwtje in één van de testen uit een vijandige omgeving (hoge populatie, weinig voedsel, veel concurrentie) en in een andere test uit een vriendelijkere omgeving.
De resultaten van de studie zijn samengevat in de onderstaande kruistabel (Tabel 12).
hamster <- matrix(c(3,17,1,13),ncol=2,byrow=TRUE)
rownames(hamster) <- c("vijandig-agressief", "vijandig-niet-agressief")
colnames(hamster) <- c("vriendelijk-agressief","vriendelijk-niet-agressief")
| vriendelijk-agressief | vriendelijk-niet-agressief | totaal | |
|---|---|---|---|
| vijandig-agressief | 3 (e) | 17 (f) | 20 |
| vijandig-niet-agressief | 1 (g) | 13 (h) | 14 |
| totaal | 4 | 30 | 34 |
De kans op de keuze voor een agressief mannetje na verblijf in een vijandige omgeving noteren we als \(\pi_1\) en kunnen we schatten als \((e+f)/n\), waarbij \(n=e+f+g+h\). De kans op de keuze voor een agressief mannetje na een vriendelijke omgeving noteren we met \(\pi_0\) en kunnen we schatten als \((e+g)/n\). Het verschil tussen beide kansen, het absoluut riscoverschil (ARV), schatten we als
\[\begin{equation*} \widehat{\text{ARV}}=\hat\pi_1-\hat\pi_0=\frac{e+f}{n}-\frac{e+g}{n}=\frac{f-g}{n} \end{equation*}\]en wordt enkel beïnvloed door de aantallen discordante paren \(f\) en \(g\). Men kan aantonen dat de standaard error van dit verschil gelijk is aan
\[\begin{equation*} \text{SE}_{\widehat{\text{ARV}}}=\frac{1}{n}\sqrt{f+g-\frac{(f-g)^2}{n}} \end{equation*}\]Als er voldoende gegevens zijn, kan men een \((1-\alpha)100\%\) betrouwbaarheidsinterval voor het absolute risicoverschil op de keuze voor een agressief mannetje t.g.v. de omgeving schatten als
\[\left[\widehat{\text{ARV}}-z_{\alpha/2}\text{SE}_{\widehat{\text{ARV}}},\widehat{\text{ARV}}+z_{\alpha/2}\text{SE}_{\widehat{\text{ARV}}}\right]\]of
\[\left[\frac{f-g}{n}-\frac{z_{\alpha/2}}{n}\sqrt{f+g-\frac{(f-g)^2}{n}},\frac{f-g}{n}+\frac{z_{\alpha/2}}{n}\sqrt{f+g-\frac{(f-g)^2}{n}}\right]\]f <- hamster[1,2]
g <- hamster[2,1]
n <- sum(hamster)
riskdiff <- (f-g)/n
riskdiff
## [1] 0.4705882
se <- sqrt(f+g-(f-g)^2/n)/n
se
## [1] 0.09517144
bi <- riskdiff + c(-1,1)*qnorm(0.975)*se
bi
## [1] 0.2840556 0.6571208
Het absolute risicoverschil op de keuze van een agressief mannetje tussen een verblijf in een vijandige en vriendelijke omgeving bedraagt
\[\begin{equation*} \widehat{\text{ARV}}=\frac{17-1}{34}=0.471 \end{equation*}\]of 47.1%. De standaard error van dit verschil is
\[\begin{equation*} \text{SE}_{\widehat{\text{ARV}}}=\frac{1}{34}\sqrt{17+1-\frac{(17-1)^2}{34}}=0.0952 \end{equation*}\]Een 95% betrouwbaarheidsinterval absolute risicoverschil op de keuze van een agressief mannetje tussen een verblijf in een vijandige en vriendelijke omgeving is bijgevolg
\[\begin{equation*} \left[0.471-1.96\times 0.0952,0.471+1.96\times 0.0952\right]=[0.284,0.658] \end{equation*}\]We hebben dus geschat dat het absolute risico met 95% kans in het interval \(28.4,65.8\)% ligt.