Determining an organism's complete genome (called genome sequencing) is one of the cornerstones of bioinformatics. Unfortunately, we still don't possess the microscope technology to zoom in to the nucleotide level and determine the sequence of a genome's nucleotides, one at a time. However, researchers can apply chemical methods to generate and identify much smaller snippets of DNA, called reads. After obtaining a large collection of reads from multiple copies of the same genome, the remaining challenge is to reconstruct the desired genome from these small pieces of DNA. This process is called genome assembly.

Even though genome sequencing now has become a multi-billion dollar enterprise, the sequencing machines that identify the reads still produce errors a substantial percentage of the time. To make matters worse, these errors are unpredictable. It is difficult to determine if the machine has made an error, let alone where in the read the error has occurred. For this reason, error correction in reads is typically a vital first step in genome assembly. As is the case with point mutations, the most common type of sequencing error occurs when a single nucleotide from a read is interpreted incorrectly.

Assignment

You are given a collection of reads of equal length. For each read $$r$$ in the data set, one of the following applies:

• $$r$$ was correctly sequenced and appears in the data set at least twice (possibly as a reverse complement¹)

• $$r$$ is incorrect (it appears in the data set exactly once) and its Hamming distance² is 1 with respect to exactly one correct read in the data set (or the reverse complement of that read); in this case, the correct read (or its reverse complement) can be used as the error correction for the incorrect read

• $$r$$ is incorrect (it appears in the data set exactly once) and has Hamming distance at least 2 with respect to all correct reads and the reverse complement of all correct reads in the data set; in that case, the incorrect read is called an orphan for which no error correction can be suggested

Your task is to determine the orphan reads and to determine the error corrections for the other incorrect reads. In order to do so, you proceed as follows:

• Write a function hamming that takes two strings. The function must throw an AssertionError with the message strings should have equal length in case both strings have a different length. Otherwise, the function must return the Hamming distance between both strings.

• Write a function complement that takes a DNA sequence (this is a string that only contains the uppercase letters A, C, G and T) as an argument. The function must return the reverse complement of the given DNA sequence.

• Write a function normalform that takes a DNA sequence as an argument. The function must either return the given sequence itself, or its reverse complement, depending on which one comes first lexicographically. We call this the normal form of the DNA sequence.

• Write a function occurrences that takes a collection (a list, tuple, …) of reads as an argument. The function must return a dictionary that maps the normal form of each read in the given collection onto the number of reads with that normal form in the given collection.

• Write a function errors that takes a collection (a list, tuple, …) of reads as an argument. The function may assume that all reads have equal length. The function must return a tuple containing two elements. The first element is the set containing all orphan reads from the given collection. The second element is the lexicographically sorted list of all other incorrect reads. Each incorrect read in that list is represented as a tuple that — apart from the incorrect read itself — also contains the corrected version of the read as a second element. Sorting only depends on the incorrect reads.

Reverse complement

The reverse complement of a DNA string is formed by reversing the string and taking the complement of each base symbol (A and T are complementary base symbols, as are C and G). We must reverse the string in addition to taking complements because of the directionality of DNA. DNA replication and transcription occurs from the 5' end to the 3' end, and the 3' end of one strand is opposite from the 5' end of the complementary strand. Thus, if we were to simply take complements, then we would be reading the second strand in the wrong direction.

Hamming distance

The Hamming distance between two strings having the same length is the minimum number of symbol substitutions required to transform one string into the other. If the strings are given by $$s_1$$ and $$s_2$$, then we write the Hamming distance between them as $$d_H(s_1,s_2)$$.

We can compute the Hamming distance by visual inspection: the Hamming distance between two strings is simply the number of positions in the strings at which corresponding symbols differ. For example, the Hamming distance between the two strings in the figure below is equal to 7.

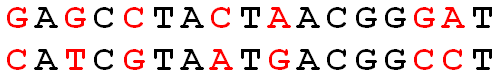
Example

>>> hamming('TTCAT', 'TTCAT')
0
>>> hamming('TTCAT', 'TTGAT')
1
>>> hamming('TTCAT', 'GAGGA')
5
>>> hamming('TTCAT', 'TTT')
Traceback (most recent call last):
AssertionError: strings should have equal length

>>> complement('TTCAT')
'ATGAA'
>>> complement('TTGAT')
'ATCAA'
>>> complement('GAGGA')
'TCCTC'

>>> normalform('TTCAT')
'ATGAA'
>>> normalform('TTGAT')
'ATCAA'
>>> normalform('GAGGA')
'GAGGA'

>>> reads = ['TCATC', 'TTCAT', 'TCATC', 'TGAAA', 'GAGGA', 'TTTCA', 'ATCAA', 'TTGAT', 'AGGCT']
>>> occurrences(reads)
{'GAGGA': 1, 'ATGAA': 1, 'TGAAA': 2, 'GATGA': 2, 'AGCCT': 1, 'ATCAA': 2}
>>> errors(reads)
({'AGGCT'}, [('GAGGA', 'GATGA'), ('TTCAT', 'TTGAT')])

>>> reads = ['GATTA', 'GATTA', 'TAATC', 'GAATC', 'GATTA', 'TAAGC', 'TAATA']
>>> occurrences(reads)
{'GATTA': 4, 'TAATA': 1, 'GCTTA': 1, 'GAATC': 1}
>>> errors(reads)
(set(), [('GAATC', 'TAATC'), ('TAAGC', 'TAATC'), ('TAATA', 'TAATC')])