Piet Mondriaan was een Nederlandse schilder die beschouwd wordt als een van de grote kunstenaars van de 20e eeuw. Sommige van Mondriaans kunstwerken hebben een unieke, geometrische stijl.

Piet Mondriaan was een Nederlandse schilder die beschouwd wordt als een van de grote kunstenaars van de 20e eeuw. Sommige van Mondriaans kunstwerken hadden een unieke, geometrische stijl.

Bij een Mondriaanse kunstpuzzel moet je een vierkant $$n \times n$$ rooster ($$n$$ rijen en $$n$$ kolommen) betegelen met niet-overlappende rechthoeken die elk een aantal vakjes van het rooster bedekken.

De afmetingen van een $$h \times b$$ rechthoek worden beschreven met twee natuurlijke getallen: het aantal rijen $$h$$ en het aantal kolommen $$b$$ van het rooster die door de rechthoek bedekt worden. De oppervlakte van een $$h \times b$$ rechthoek is gelijk aan het aantal bedekte vakjes: $$h \times b$$. Het is niet toegelaten om twee rechthoeken met dezelfde afmetingen te gebruiken: als je een deel van het rooster bedekt met een $$h \times b$$ rechthoek, dan mag de betegeling geen andere $$h \times b$$ of $$b \times h$$ rechthoeken meer gebruiken. Een betegeling mag wel twee rechthoeken met dezelfde oppervlakte hebben.

De score van een betegeling is gelijk aan de oppervlakte van de grootste rechthoek min de oppervlakte van de kleinste rechthoek. Het doel is om een betegeling te vinden met een zo klein mogelijke score.

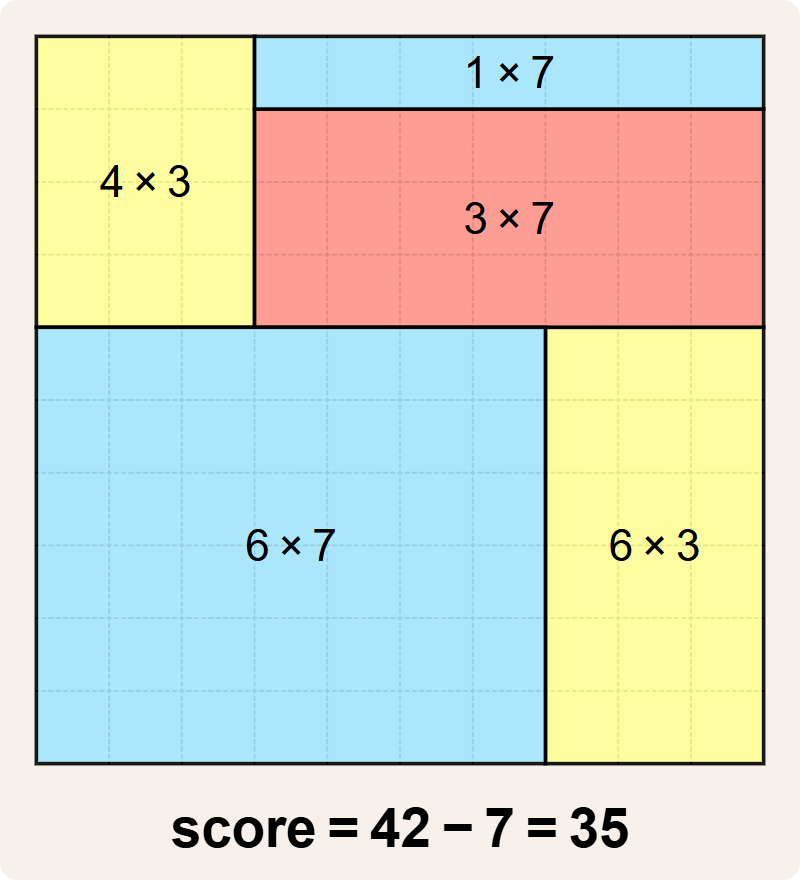
Dit is bijvoorbeeld een betegeling van een $$10 \times 10$$ rooster met score $$42 - 7 = 35$$.

Betegeling van een $$10 \times 10$$ rooster met score $$42 - 7 = 35$$.

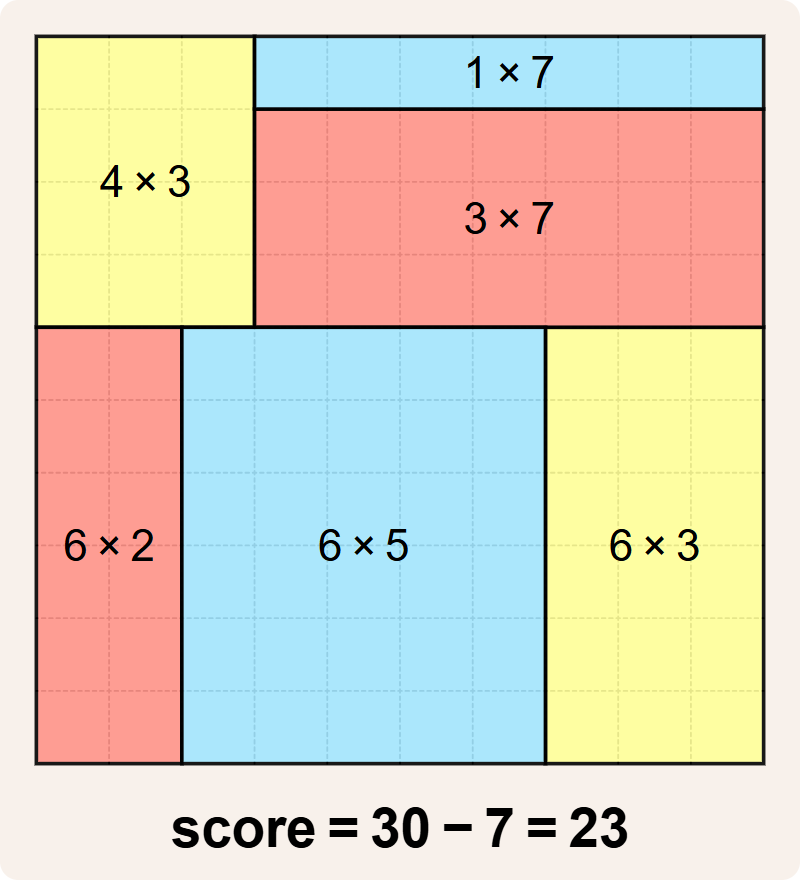
Er zijn echter betere betegelingen mogelijk. Dit is bijvoorbeeld een betegeling met score $$30 - 7 = 23$$. Dat is nog steeds suboptimaal, maar al beter dan wat we hadden.

Betegeling van een $$10 \times 10$$ rooster met score $$30 - 7 = 23$$.

Merk op dat de $$4 \times 3$$ rechthoek en de $$6 \times 2$$ rechthoek weliswaar dezelfde oppervlakte hebben ($$12$$), maar dit is een geldige betegeling omdat ze verschillende afmetingen hebben. Er is echter nog een betere betegeling met score $$25 - 7 = 18$$.

Betegeling van een $$10 \times 10$$ rooster met score $$25 - 7 = 18$$.

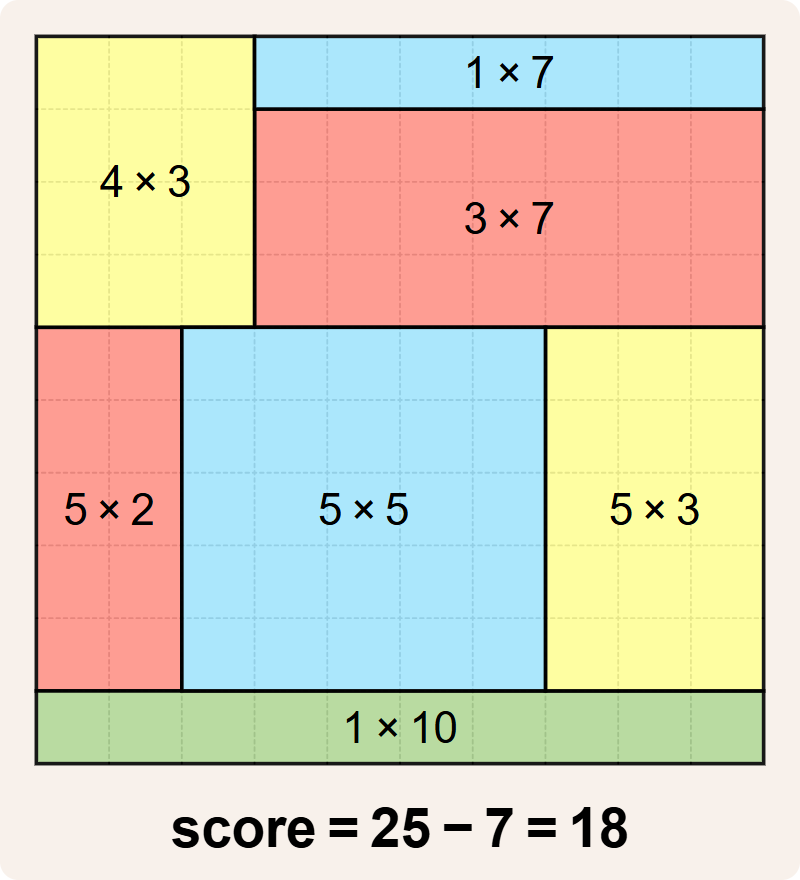
Onderstaande betegeling lijkt de beste die we tot nu toe gevonden hebben, maar dat is ze niet. Ze voldoet immers niet aan de regel dat een betegeling geen rechthoeken met dezelfde afmetingen mag hebben. De betegeling heeft een $$4 \times 3$$ rechthoek en een $$3 \times 4$$ rechthoek, en dat is niet toegelaten. De $$5 \times 2$$ rechthoek en de $$1 \times 10$$ rechthoek hebben dezelfde oppervlakte ($$10$$), maar omdat ze verschillende afmetingen hebben is dat geen inbreuk tegen de regels voor betegelingen.

Ongeldige betegeling van een $$10 \times 10$$ rooster: ze voldoet niet aan de regel dat een betegeling geen rechthoeken met dezelfde afmetingen mag hebben. De betegeling heeft een $$4 \times 3$$ rechthoek en een $$3 \times 4$$ rechthoek, en dat is niet toegelaten. De $$5 \times 2$$ rechthoek en de $$1 \times 10$$ rechthoek hebben dezelfde oppervlakte (10), maar omdat ze verschillende afmetingen hebben is dat geen inbreuk tegen de regels voor betegelingen.

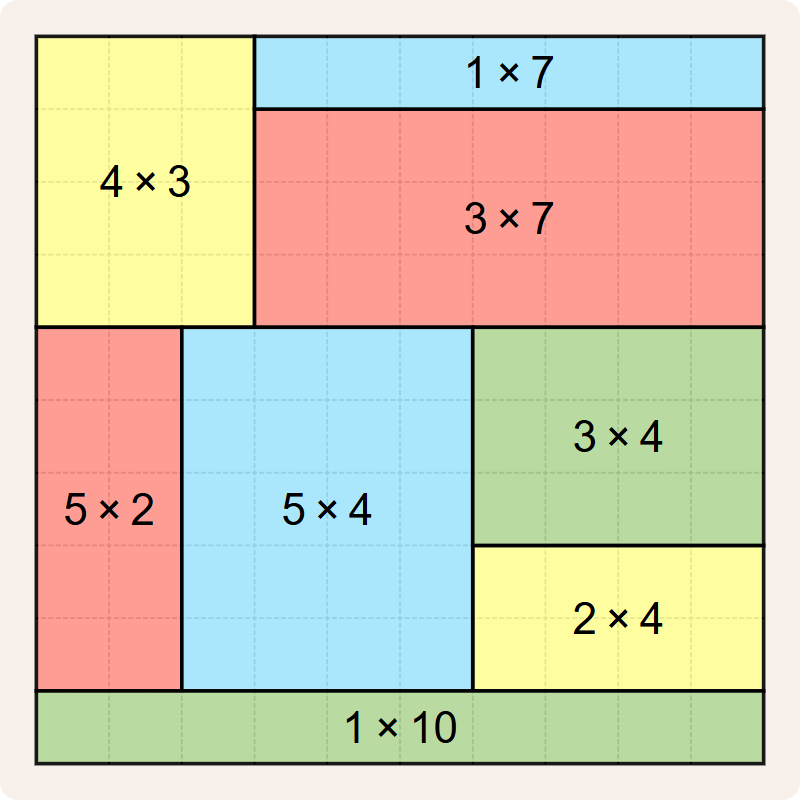
Als bonus hebben we alle rechthoeken ingekleurd met zo weinig mogelijk kleuren, zodat twee rechthoeken met dezelfde kleur nooit een gemeenschappelijk zijde of een gemeenschappelijk hoekpunt hebben.

Opgave

Schrijf een bash shell script mondrian waarmee een grafische voorstelling (SVG) van de betegeling van een vierkant $$n \times n$$ rooster ($$n$$ rijen en $$n$$ kolommen) kan uitgeschreven worden naar standaard uitvoer (stdout). Aan het script moet je de padnaam doorgeven van een configuratiebestand dat een geldige betegeling beschrijft volgens de regels van de Mondriaanse kunstpuzzels. Het script mag ervan uitgaan dat er een leesbaar tekstbestand wordt doorgegeven dat een geldige betegeling beschrijft, zonder dat dit expliciet moet gecontroleerd worden. Verderop¹ bespreken we stap voor stap hoe deze SVG-afbeelding opgebouwd wordt. Het script moet bijvoorbeeld kunnen gebruikt worden om de afbeeldingen uit de inleiding van deze opgave te genereren. Deze afbeelding

Betegeling van een $$8 \times 8$$ rooster met score $$12 - 6 = 6$$.

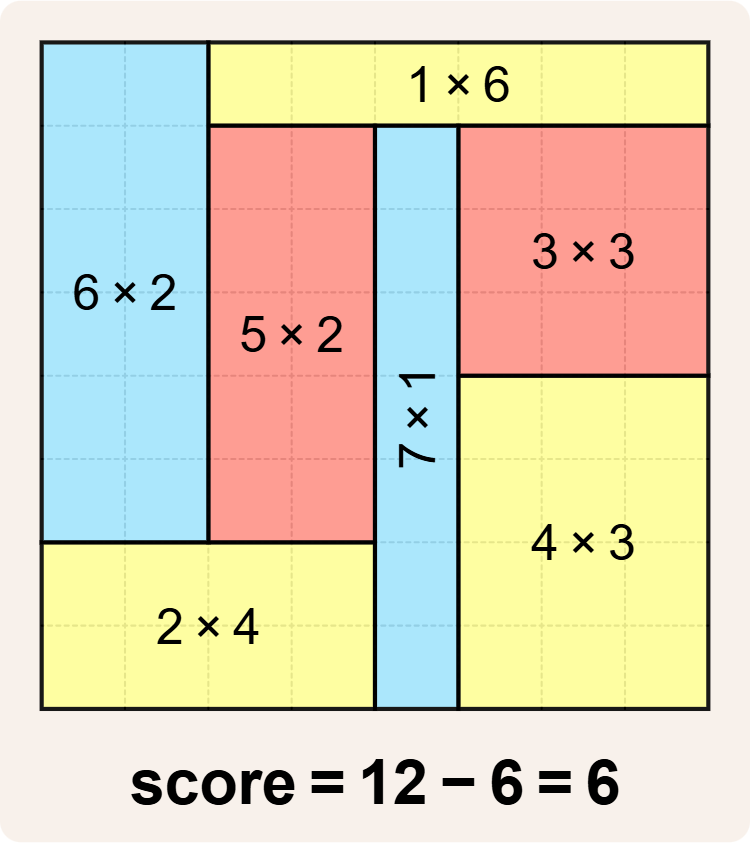
kan bijvoorbeeld gegenereerd worden op basis van dit configuratiebestand (puzzle_8_score_6.png²):

8
# yellow rectangles
0 2 1 6 #FFFF99
6 0 2 4 #FFFF99
4 5 4 3 #FFFF99
# red rectangles
1 2 5 2 #FF9389
1 5 3 3 #FF9389
# blue rectangles
0 0 6 2 #A3E6FE
1 4 7 1 #A3E6FE

De eerste regel bevat de dimensie $$n \in \mathbb{N}_0$$ van het vierkant rooster (in dit geval een $$8 \times 8$$ rooster). Om naar de vakjes in het rooster te kunnen verwijzen, nummeren we de rijen van het rooster van boven naar onder en de kolommen van links naar rechts, telkens vanaf nul. Op die manier kunnen we de positie van een vakje aanduiden met nummer van de rij $$r$$ ($$0 \leq r < n$$) en het nummer van de kolom $$k$$ ($$0 \leq k < n$$) waarop het vakje gelegen is in het rooster.

Daarna volgen een aantal regels die één rechthoek uit de betegeling beschrijven aan de hand van vijf informatievelden die door spaties van elkaar gescheiden worden:

het rijnummer $$r$$ van het vakje in het rooster dat bedekt wordt door de linkerbovenhoek van de rechthoek
het kolomnummer $$k$$ van het vakje in het rooster dat bedekt wordt door de linkerbovenhoek van de rechthoek
het aantal rijen $$h$$ van het rooster die door de rechthoek bedekt worden
het aantal kolommen $$b$$ van het rooster die door de rechthoek bedekt worden
de kleur van de rechthoek (een geldige HTML-kleur³)

Regels die starten met een hekje beschrijven geen rechthoek en moeten genegeerd worden. Voor het voorbeeld configuratiebestand moet het script deze SVG-afbeelding uitschrijven:

        <svg xmlns="http://www.w3.org/2000/svg" width="450" height="500" viewBox="-0.5 -0.5 9 10">
<style type="text/css">
text{font-family:consolas;text-anchor:middle;dominant-baseline:middle;fill:black}
.grid{stroke:black;stroke-width:0.025;stroke-linecap:round;stroke-dasharray:0.05;stroke-dashoffset:0.025}
.rectangle{stroke:black;stroke-width:0.05;opacity:0.9}
</style>
<rect x="-0.5" y="-0.5" width="9" height="10" fill="#F8F1EB" rx="0.2" />
<path class="grid" d="M0,1H8M0,2H8M0,3H8M0,4H8M0,5H8M0,6H8M0,7H8" />
<path class="grid" d="M1,0V8M2,0V8M3,0V8M4,0V8M5,0V8M6,0V8M7,0V8" />
<rect class="rectangle" x="2" y="0" width="6" height="1" fill="#FFFF99" />
<text x="5.0" y=".5" font-size="0.6">1 × 6</text>
<rect class="rectangle" x="0" y="6" width="4" height="2" fill="#FFFF99" />
<text x="2.0" y="7.0" font-size="0.6">2 × 4</text>
<rect class="rectangle" x="5" y="4" width="3" height="4" fill="#FFFF99" />
<text x="6.5" y="6.0" font-size="0.6">4 × 3</text>
<rect class="rectangle" x="2" y="1" width="2" height="5" fill="#FF9389" />
<text x="3.0" y="3.5" font-size="0.6">5 × 2</text>
<rect class="rectangle" x="5" y="1" width="3" height="3" fill="#FF9389" />
<text x="6.5" y="2.5" font-size="0.6">3 × 3</text>
<rect class="rectangle" x="0" y="0" width="2" height="6" fill="#A3E6FE" />
<text x="1.0" y="3.0" font-size="0.6">6 × 2</text>
<rect class="rectangle" x="4" y="1" width="1" height="7" fill="#A3E6FE" />
<text x="4.5" y="4.5" font-size="0.6" transform="rotate(-90 4.5 4.5)">7 × 1</text>
<text x="4.0" y="8.75" font-size="0.6" font-weight="bold">score = 12 - 6 = 6</text>
</svg>

Opbouw van de SVG-afbeelding

Scalable Vector Graphics (SVG⁴) is een op XML⁵ gebaseerd bestandsformaat dat vectorafbeeldingen⁶ tekstueel beschrijft aan de hand van eenvoudige meetkundige bouwstenen zoals punten, lijnen, cirkels en veelhoeken.

Je moet geen SVG of XML kennen om deze opgave op te lossen. We bespreken stap voor stap hoe de grafische voorstelling van de schaakbordopstelling in SVG-formaat opgebouwd wordt aan de hand van vijf sjablonen: hoofding⁷, rooster⁸, rechthoek⁹, score¹⁰ en voettekst¹¹. Daarbij zullen we de variabele onderdelen van elk sjabloon in het groen weergeven. Daar moet het script de juiste waarden invullen. Het is belangrijk dat elk sjabloon exact overgenomen wordt zodat het resultaat dat het script uitschrijft precies overeenkomt met de beschreven specificatie.

Hoofding

<svg xmlns="http://www.w3.org/2000/svg" width="450" height="500" viewBox="-0.5 -0.5 9 10">
<style type="text/css">
text{font-family:consolas;text-anchor:middle;dominant-baseline:middle;fill:black}
.grid{stroke:black;stroke-width:0.025;stroke-linecap:round;stroke-dasharray:0.05;stroke-dashoffset:0.025}
.rectangle{stroke:black;stroke-width:0.05;opacity:0.9}
</style>
<rect x="-0.5" y="-0.5" width="9" height="10" fill="#F8F1EB" rx="0.2" />

Dit sjabloon voor de hoofding bevat de SVG start-tag (svg) en algemene opmaak van de afbeelding (style). Het tekent ook een rechthoek (rect) als achtergrond. De breedte van de afbeelding is gelijk aan $$n + 1$$ en moet in het sjabloon zowel ingevuld worden als derde waarde van de viewBox en als waarde voor het width-attribuut van het rect-element. De hoogte van de afbeelding is gelijk aan $$n + 2$$ en moet in het sjabloon zowel ingevuld worden als vierde waarde van de viewBox en als waarde voor het height-attribuut van het rect-element. Het width-attribuut en het height-attribuut van de SVG start-tag (svg) moeten respectievelijk ingevuld worden met 50 keer de breedte en 50 keer de hoogte van de afbeelding.

Rooster

<path class="grid" d="M0,1H8M0,2H8M0,3H8M0,4H8M0,5H8M0,6H8M0,7H8" />
<path class="grid" d="M1,0V8M2,0V8M3,0V8M4,0V8M5,0V8M6,0V8M7,0V8" />

De eerste regel van het sjabloon tekent de horizontale roosterlijnen. De waarde van het d-attribuut moet ingevuld worden met een aaneenschakeling van het patroon M0,yHn waarbij y loopt van $$1$$ tot $$n$$ en n gelijk is aan de dimensie $$n$$ van het rooster.

De tweede regel van het sjabloon tekent de verticale roosterlijnen. De waarde van het d-attribuut moet ingevuld worden met een aaneenschakeling van het patroon Mx,0Vn waarbij x loopt van $$1$$ tot $$n$$ en n gelijk is aan de dimensie $$n$$ van het rooster.

Rechthoek

<rect class="rectangle" x="2" y="0" width="6" height="1" fill="#FFFF99" />
<text x="5.0" y=".5" font-size="0.6">1 × 6</text>

De eerste regel van het sjabloon tekent een gekleurde rechthoek (rect). Het rijnummer $$r$$ (y), het kolomnummer $$k$$ (x), het aantal rijen $$h$$ (height), het aantal kolommen $$b$$ (width) en de kleur van de rechthoek (fill) kunnen rechtstreeks overgenomen worden uit het configuratiebestand en ingevuld worden als waarden voor de corresponderende attributen van het rect-element.

De tweede regel van het sjabloon plaatst een tekstuele beschrijving (text) van de afmetingen van de rechthoek in het zwaartepunt¹² van de rechthoek. De inhoud van het text-element gebruikt het patroon h × b, waarbij h ingevuld wordt met de het aantal rijen $$h$$ en b ingevuld wordt met het aantal kolommen $$b$$ van de rechthoek. Voor de positionering van het text-element wordt de waarde van het x-attribuut berekend als \[ k + \frac{b}{2} \] en wordt de waarde van het y-attribuut berekend als \[ r + \frac{h}{2} \] Dit zijn reële getallen die altijd moeten uitgeschreven worden met één decimaal cijfer. Als het deel voor het decimale punt van een reeël getal gelijk is aan nul, dan gebruiken we een verkorte notatie waarbij er niets voor het decimale punt staat (dus bijvoorbeeld .5 in plaats van 0.5).

Als de breedte van de rechthoek maar één kolom beslaat, dan krijgt het text-element een extra transform-attribuut om ervoor te zorgen dat de tekst 90° in tegenwijzerzin gedraaid wordt rond het punt waar de tekst geplaatst wordt. De tweede regel van het sjabloon wordt dan

<text x="4.5" y="4.5" font-size="0.6" transform="rotate(-90 4.5 4.5)">7 × 1</text>

Het transform-attribuut roept de rotate-functie aan met drie argumenten: de waarde -90 (90° in tegenwijzerin) en twee argumenten waarvan de waarde gelijk is aan de waarden die toegekend worden aan het x-attribuut en het y-attribuut van het text-element (met dezelfde formattering voor reële getallen).

Voor elke rechthoek in het configuratiebestand moeten twee regels toegevoegd worden aan de SVG-afbeelding, die wordt opgemaakt volgens het sjabloon. In de SVG-afbeelding moeten de rechthoeken in dezelfde volgorde opgelijst worden als in het configuratiebestand.

Score

<text x="4.0" y="8.75" font-size="0.6" font-weight="bold">score = 12 - 6 = 6</text>

Dit sjabloon plaatst een tekstuele beschrijving (text) van de score van de betegeling onder het rooster. De inhoud van het text-element gebruikt het patroon grootste - kleinste = score, waarbij de cursieve fragmenten respectievelijk ingevuld worden met i) de oppervlakte van de grootste rechthoek in de betegeling, ii) de oppervlakte van de kleinste rechthoek in de betegeling en iii) de score van de betegeling. Voor de positionering van het text-element wordt de waarde van het x-attribuut berekend als \[ \frac{n}{2} \] en wordt de waarde van het y-attribuut berekend als \[ n + 0.75 \] Dit zijn reële getallen die altijd moeten uitgeschreven worden met één decimaal cijfer. Als het deel voor het decimale punt van een reeël getal gelijk is aan nul, dan gebruiken we een verkorte notatie waarbij er niets voor het decimale punt staat (dus bijvoorbeeld .5 in plaats van 0.5).

Voettekst

</svg>

Dit laatste sjabloon sluit de SVG-afbeelding af met een SVG stop-tag.

Voorbeeld

        $ mondrian puzzle_8_score_6.txt
<svg xmlns="http://www.w3.org/2000/svg" width="450" height="500" viewBox="-0.5 -0.5 9 10">
<style type="text/css">
text{font-family:consolas;text-anchor:middle;dominant-baseline:middle;fill:black}
.grid{stroke:black;stroke-width:0.025;stroke-linecap:round;stroke-dasharray:0.05;stroke-dashoffset:0.025}
.rectangle{stroke:black;stroke-width:0.05;opacity:0.9}
</style>
<rect x="-0.5" y="-0.5" width="9" height="10" fill="#F8F1EB" rx="0.2" />
<path class="grid" d="M0,1H8M0,2H8M0,3H8M0,4H8M0,5H8M0,6H8M0,7H8" />
<path class="grid" d="M1,0V8M2,0V8M3,0V8M4,0V8M5,0V8M6,0V8M7,0V8" />
<rect class="rectangle" x="2" y="0" width="6" height="1" fill="#FFFF99" />
<text x="5.0" y=".5" font-size="0.6">1 × 6</text>
<rect class="rectangle" x="0" y="6" width="4" height="2" fill="#FFFF99" />
<text x="2.0" y="7.0" font-size="0.6">2 × 4</text>
<rect class="rectangle" x="5" y="4" width="3" height="4" fill="#FFFF99" />
<text x="6.5" y="6.0" font-size="0.6">4 × 3</text>
<rect class="rectangle" x="2" y="1" width="2" height="5" fill="#FF9389" />
<text x="3.0" y="3.5" font-size="0.6">5 × 2</text>
<rect class="rectangle" x="5" y="1" width="3" height="3" fill="#FF9389" />
<text x="6.5" y="2.5" font-size="0.6">3 × 3</text>
<rect class="rectangle" x="0" y="0" width="2" height="6" fill="#A3E6FE" />
<text x="1.0" y="3.0" font-size="0.6">6 × 2</text>
<rect class="rectangle" x="4" y="1" width="1" height="7" fill="#A3E6FE" />
<text x="4.5" y="4.5" font-size="0.6" transform="rotate(-90 4.5 4.5)">7 × 1</text>
<text x="4.0" y="8.75" font-size="0.6" font-weight="bold">score = 12 - 6 = 6</text>
</svg>