An example of a recursive definition is the definition of the factorial, which was already introduced in the previous two chapters. In those chapters I gave the following definition of the factorial: The factorial of a positive integer is that integer, multiplied by all positive integers that are lower (excluding zero).

Mathematicians prefer the recursive definition: The factorial \(n!\) of any positive integer \(n\) is calculated as follows: \(1! = 1\), and \(n! = n * (n-1)!\) for \(n > 1\).

This definition is recursive as it refers to the factorial of \(n-1\) to define the factorial of \(n\). This is not leading to an endless recursion, however, as at some point \(n\) will be \(1\), and the factorial of \(1\) is defined separately.

You can implement the factorial as a recursive function as follows:

def factorial( n ):
    if n <= 1:
        return 1
    return n * factorial( n-1 )

print( factorial( 5 ) )

Notice how this function describes the recursive definition of the factorial exactly: if n is 1, it returns 1, and otherwise it returns n times the factorial of n-1. (Note that I wrote if n <= 1 instead of n == 1 to avoid problems with the user calling the function with, for instance, a negative n.)

In case you have troubles understanding what happens in this function, let’s describe the details of the calls it makes. I have indented calls that are made while a “high level” call is still active. A return statement which is indented one level deeper than a call statement is given in that call and returns from it with the specified value.

call factorial( 5 )
    call factorial( 4 )
        call factorial( 3 )
            call factorial( 2 )
                call factorial( 1 )
                    return 1
                return 2 * 1
            return 3 * 2
        return 4 * 6
    return 5 * 24
print( 120 )

When to use recursive implementations

Once you understand the recursive implementation of the factorial, it might look appealing. It is simple, elegant, and has a certain coolness factor. However, the iterative implementation of the factorial is highly preferable over the recursive one.

The reason is clear from the call descriptions above. You see that before the call to factorial( 1 ) is made, four other calls to factorial() already reside in memory. Should you wish to calculate the factorial of 100, no less than 100 calls to the function will reside in memory before it can start returning values. This is not a good idea, and, in fact, Python may easily run out of (stack) memory in such a case, or become really, really slow.

Contrariwise, an iterative implementation of the factorial only needs to keep two variables in memory. It is fast and there is no danger of crashing.

So you should only use recursive implementations if:

• recursion is the most natural way to implement the solution; and

• the recursive process is guaranteed not to go too deep.

Any recursive process can also be implemented as an iterative process. However, occasionally you can encounter problems for which the recursive solution is much more elegant, readable, and maintainable than the iterative one. In that case, consider reverting to the recursive solution.

Searching a maze

At this point in the book it is hard to give a good demonstration of recursion, as it needs particular data structures to show its power. But to still show something non-trivial, I have created a module called pcmaze. You can find it in Appendix 32, and you need to either create it or download it from the same place where you got pcinput.py to be able to run the code in this subsection.

pcmaze implements a simple maze, which connects some numbered cells. You can ask for the maze’s entrance using the function entrance(). The maze’s exit is given by the function exit() (not to be confused with the exit() function from sys). The module also has a function connected() that gets two numeric arguments: it returns True if there is a direct connection between the cells with those numbers, and False otherwise. The entrance is guaranteed to be the lowest-numbered cell, while the exit is guaranteed to be the highest-numbered cell.

The goal is to write some code that finds the way from the entrance to the exit (if there is such a way). The maze is visualized in Figure 10.1¹. Entrance is 1, exit is 16.

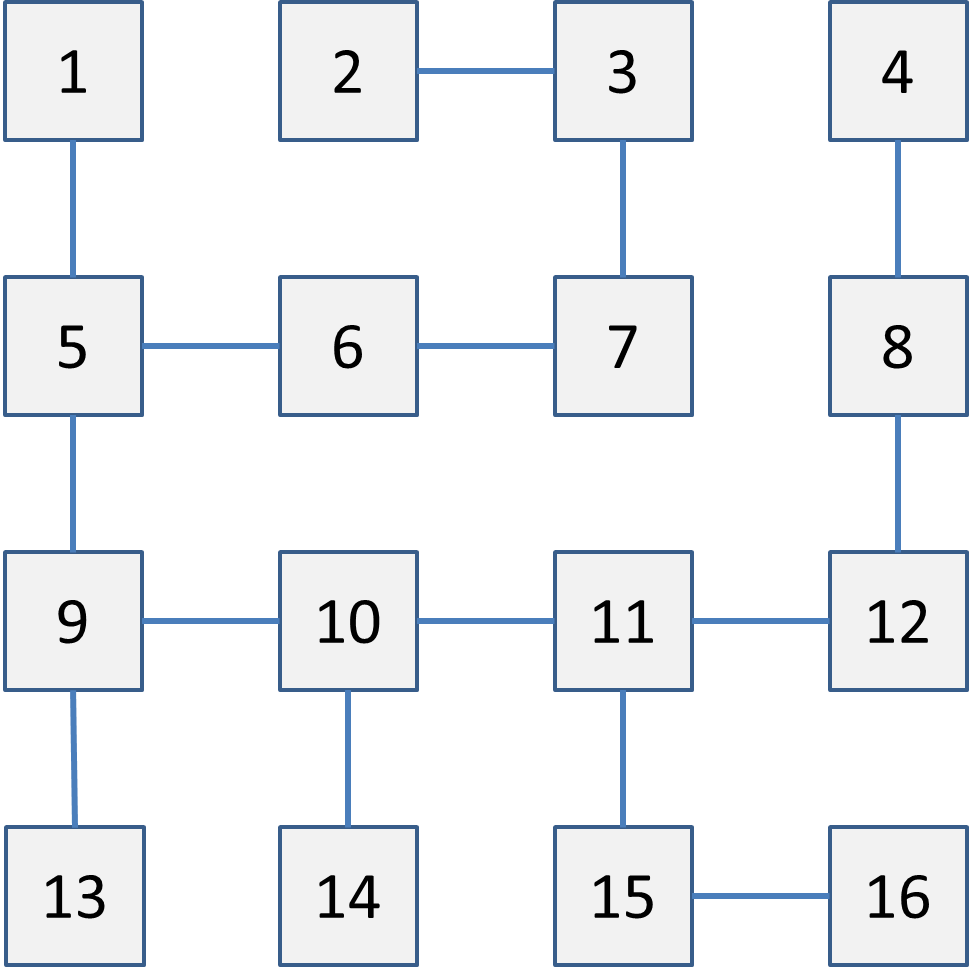
So how do you find a way through such a maze (without knowing the exact layout)? Recursively, you can do it as follows: You define a function leads_to_exit() that returns a path to the exit if the cell that it is currently examining is on the path that leads to the exit. If that function returns a path, then you know that the current cell is also on the path. If you call it with cell 1, you get a path that leads from the entrance to the exit (if there is such a path).

But how does that function know if a cell is part of a path that leads to the exit? Well, if the current cell actually is the exit, then yes, it leads to the exit. If not, then it leads to the exit if it has a connection with a cell that leads to the exit. This is a recursive definition.

You have to be careful that such a recursive definition cannot get stuck in a circular path in the maze. That means that when the function moves from cell A to cell B, it is not allowed to move back. If that is taken care of, the function should work. It wouldn’t work if there would be circular paths in the maze, but fortunately there aren’t. The problem is not unsolvable if there are circular paths, but to solve it a data structure is needed that is not discussed yet.

In pseudo-code, the recursive function leads_to_exit() is something like this:

function leads_to_exit( currentcell ):
    if (currentcell is the exit):
        return (path consisting of only the exit)
    for (every connnectedcell that was not yet explored):
        path = leads_to_exit( connectedcell )
        if (path is not empty):
            add currentcell to path
            return path
    return (empty path)

Now let’s implement this recursive solution. In the implementation immediately below, the path will not be returned, but I return just True or False to indicate that the path is found or not, and I print the path in the function itself (a bit further down I provide the complete implementation for the pseudo-code above).

from pcmaze import entrance, exit, connected

def leads_to_exit( comingfrom, cell ):
    if cell == exit():
        return True
    for i in range( entrance(), exit()+1 ):
        if i == comingfrom:
            continue
        if not connected( cell, i ):
            continue
        if leads_to_exit( cell, i ):
            print( cell, "->", i )
            return True
    return False

if leads_to_exit( 0, entrance() ):
    print( "Path found!" )
else:
    print( "Path not found" )

Let’s look at the recursive function in detail.

It gets two parameters. The first is the cell that the path is coming from. The second is the cell that is checked to see if it leads to the exit. The first parameter is only needed because returning on the path is not allowed.

The function first checks if the exit is reached. If it is, it returns True.

If the exit is not reached, the function checks all cells of the maze as possible follow-up cells.

It excludes (a) the cell that it just arrived from; and (b) all the cells to which there are no connections. But it checks all the other cells. There is no need to explicitly exclude the cell itself, as in the definition of the maze a cell is not connected to itself.

As soon as it finds a cell for which a recursive call to the function says that it leads to the exit, while coming from the current cell, it prints that movement and returns True. This indicates to the call that arrived here that, yes, a path is found.

Otherwise, once it has checked all possible follow-up connections and no path was found, it returns False.

This process prints the whole path from entrance to exit, in reverse order.

To make clear what is happening, I have expanded the function a bit, now also printing every connection that is checked. I have also included a depth parameter, that keeps track of how deep the recursion is going. I translate that into indentations.

from pcmaze import entrance, exit, connected

def leads_to_exit( comingfrom, cell, depth ):
    indent = depth * 4 * " "
    if cell == exit():
        return True
    for i in range( entrance(), exit()+1 ):
        if i == comingfrom:
            continue
        if not connected( cell, i ):
            continue
        print( indent + "Check connection", cell, "->", i )
        if leads_to_exit( cell, i, depth + 1 ):
            print( indent + "Path found:", cell, "->", i )
            return True
    return False

if leads_to_exit( 0, entrance(), 0 ):
    print( "Path found!" )
else:
    print( "Path not found" )

Return values of recursive functions

Just like regular functions, recursive functions can communicate information to the rest of the program using their return values.

One of the less nice things about the maze-solving recursive functions above is that they print the path (rather than return it), and that the path is printed in reverse order. It would be better if, instead, the function calls returned their part of the path to the higher level calls, so that the path as a whole is returned from the first call, in the main program. This is what the pseudo-code above proposed. A good way to return a path is in the form of a list, but lists will be discussed in Chapter 13. Instead, I will do it in the form of a string.

It works as follows: A call that finds the exit cell, returns the number of the exit cell as a string. Any call that finds part of the path, returns what it got returned itself, but adds the current cell to that path. Any call that finds nothing, returns nothing, i.e., an empty string.

This means that in the recursive functions above, any return True will instead return a string containing a (partial) path, and any return False returns an empty string. The code becomes the following:

from pcmaze import entrance, exit, connected

def leads_to_exit( comingfrom, cell ):
    if cell == exit():
        return "{}".format( exit() )
    for i in range( entrance(), exit()+1 ):
        if i == comingfrom:
            continue
        if not connected( cell, i ):
            continue
        check = leads_to_exit( cell, i )
        if check != "":
            return "{} -> {}".format( cell, check )
    return ""

check = leads_to_exit( 0, entrance() )
if check != "":
    print( "Path found!", check )
else:
    print( "Path not found" )

If you want to understand recursion, study this code closely. This code represents a typical use of return values in recursive functions. Students whose understanding of recursion is wonky and who get an assignment that has them communicate information from a deeper level recursive call to a higher level one, often revert to using a global variable. As you can see, that is not necessary.

All in all, there is no real difference between a recursive function call and a regular function call, except that you have to be careful that recursive calls terminate at some point. It only looks strange the first time that you encounter it.