Genoomassemblage is het computationele proces waarbij de genoomsequentie van een organisme bepaald wordt. Onderzoekers zijn momenteel nog niet in staat om de nucleotiden van een volledig genoom in één keer te bepalen. In plaats daarvan doen ze een beroep op hoogtechnologische chemische methoden om de basenvolgorde te bepalen van korte stukjes DNA (doorgaans minder dan 1000 bp lang). Deze korte stukjes worden de reads genoemd.

genome assembly
Genoomassemblage werkt door veel kopieën van hetzelfde genoom in kleinere, identificeerbare reads op te breken, waaruit dan op een computationele manier één enkele kopie van het genoom samengesteld wordt.

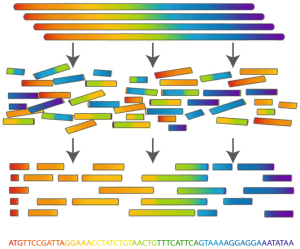
Om een volledig genoom te sequeneren, gaan onderzoekers verschillende kopieën van het genoom als het ware chemisch opblazen, waardoor elk van de bekomen reads door een sequenator kan uitgelezen worden. Om het genoom terug te reconstrueren, wordt gebruikgemaakt van de overlap tussen de reads om te bepalen welke reads naast elkaar op het genoom liggen. Als bijvoorbeeld de korte reads GACCTACA en ACCTACAA uitgelezen worden, dan kunnen we uit het feit dat ze overlappen, afleiden dat beide afkomstig zijn van het DNA fragment GACCTACAA.

In deze opgave lossen we een vereenvoudige versie van genoomassemblage-probleem op, waarbij alle reads vaste lengte $$k$$ hebben ($$k$$-meren), alle $$k$$-meren uit het oorspronkelijke genoom juiste één keer voorkomen en er geen leesfouten voorkomen in de reads.

Opgave

We bepalen eerst alle $$k$$-meren van een woord van lengte $$n$$. Dit zijn de $$n - k + 1$$ overlappende substrings met vaste lengte $$k$$. Daarna schudden we deze $$k$$-meren willekeurig door elkaar, en moet je proberen om het originele woord terug te reconstrueren op basis van de overlap tussen de $$k$$-meren. Beschouw bijvoorbeeld de volgende vier substrings van lengte 3 (hier weergegeven in alfabetische volgorde):

ANA ANA BAN NAN

Dit zijn de vier 3-meren van het woord BANANA. Gevraagd wordt:

Ondanks het feit dat dit een sterk vereenvoudigde versie is van het echte genoomassemblage-probleem, is het op zich al vrij uitdagend om met een efficiënte oplossing op de proppen te komen. De opdracht bestaat er immers niet enkel in om een implementatie te vinden die minstens één oplossing kan vinden, maar ook om die implementatie zo snel mogelijk te maken. In het artikel van Compeau et al. (2011) vind je de nodige inspiratie om het probleem efficiënt aan te pakken. In de praktijk worden genoomassemblages typisch uitgevoerd op een paar miljoen reads van 40 tot 10.000 baseparen (afhankelijk van de gebruikte technologie voor het sequeneren), waarmee genoomsequenties in grootteorde van miljoenen of miljarden baseparen moeten samengesteld worden.

Voorbeeld

>>> kmeren('banana', 2)
['ba', 'an', 'na', 'an', 'na']
>>> kmeren('cucumber', 2)
['cu', 'uc', 'cu', 'um', 'mb', 'be', 'er']
>>> kmeren('elderberry', 3)
['eld', 'lde', 'der', 'erb', 'rbe', 'ber', 'err', 'rry']
>>> kmeren('pineapple', 3)
['pin', 'ine', 'nea', 'eap', 'app', 'ppl', 'ple']
>>> kmeren('mississippi', 3)
['mis', 'iss', 'ssi', 'sis', 'iss', 'ssi', 'sip', 'ipp', 'ppi']
>>> kmeren('alfalfa', 3)
['alf', 'lfa', 'fal', 'alf', 'lfa']

>>> assembleer(['an', 'an', 'ba', 'na', 'na'])
'banana'
>>> assembleer(['be', 'cu', 'cu', 'er', 'mb', 'uc', 'um'])
'cucumber'
>>> assembleer(['ber', 'der', 'eld', 'erb', 'err', 'lde', 'rbe', 'rry'])
'elderberry'
>>> assembleer(['app', 'eap', 'ine', 'nea', 'pin', 'ple', 'ppl'])
'pineapple'
>>> assembleer(['ipp', 'iss', 'iss', 'mis', 'ppi', 'sip', 'sis', 'ssi', 'ssi'])
'mississippi'
>>> assembleer(['alf', 'alf', 'fal', 'lfa', 'lfa'])
'alfalfa'

Uitdaging

Je hebt nu een algoritme geïmplementeerd waarmee woorden kunnen gereconstrueerd woorden op basis van een willekeurig geordende lijst van al hun $$k$$-meren. De vraag die zich nu stelt is hoe snel en hoe robuust je implementatie is. Het bestand words8.txt1 bevat een lijst van 70.000+ Engelse woorden van minstens 8 karakters, waarbij elk woord op een afzonderlijke regel staat. Gebruik je implementatie om elk woord in deze lijst uit te lezen, op te splitsen in al zijn $$k$$-meren (kies zelf een vaste $$k$$; hoe kleiner $$k$$ hoe moeilijker het probleem), de $$k$$-meren willekeurig door elkaar te schudden en daarna het oorspronkelijke woord te reconstrueren op basis van de lijst van $$k$$-meren. Analyseer het gedrag van je "assemblage"-programma:

Bronnen