De chef-kok van een restaurant is nogal van het slordige type. Als hij een stapel pannenkoeken moet bakken dan zijn er nooit twee pannenkoeken met dezelfde grootte. De maitre d'hotel eist echter dat de kelners alle pannenkoeken in een stapel eerst van klein naar groot sorteren — met de kleinste pannenkoek van boven en de grootste van onder — voor ze die naar de tafelgasten brengen.

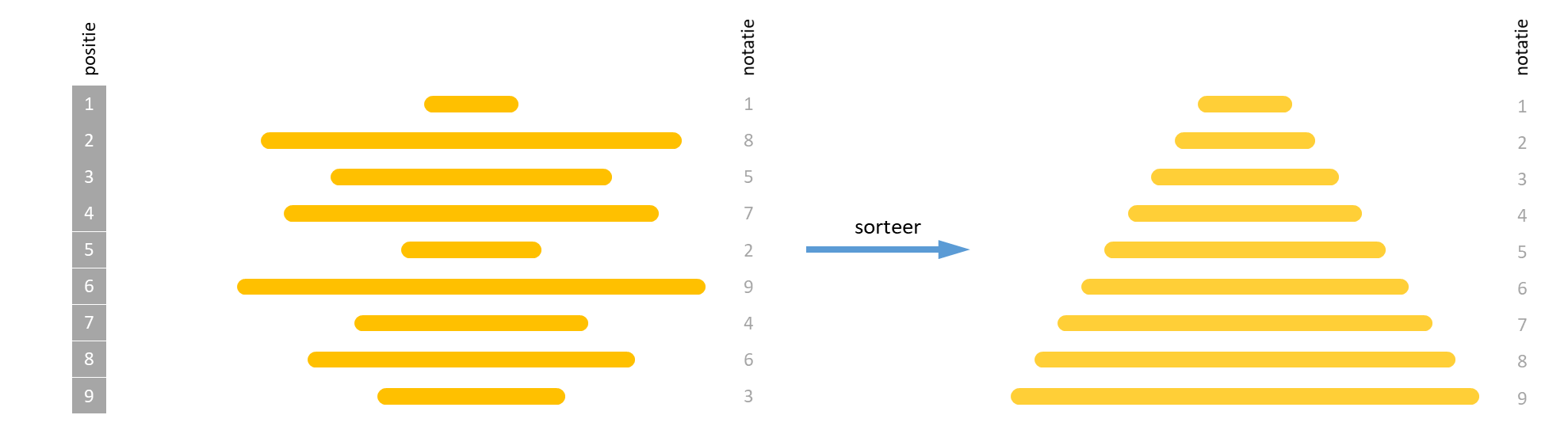
Om een stapel pannenkoeken te sorteren, kunnen de kelners echter slechts één handeling uitvoeren: ze schuiven een spatel onder één van de pannenkoeken in de stapel, wentelen alle pannenkoeken op de spatel samen om en leggen die terug bovenop het resterende deel van de stapel. Ze kunnen deze handeling verschillende keren na elkaar uitvoeren, waarbij ze de spatel telkens onder een andere pannenkoek kunnen schuiven. Om snel te kunnen werken, maken de kelners er een sport van om een stapel te sorteren met zo weinig mogelijk wentelingen.

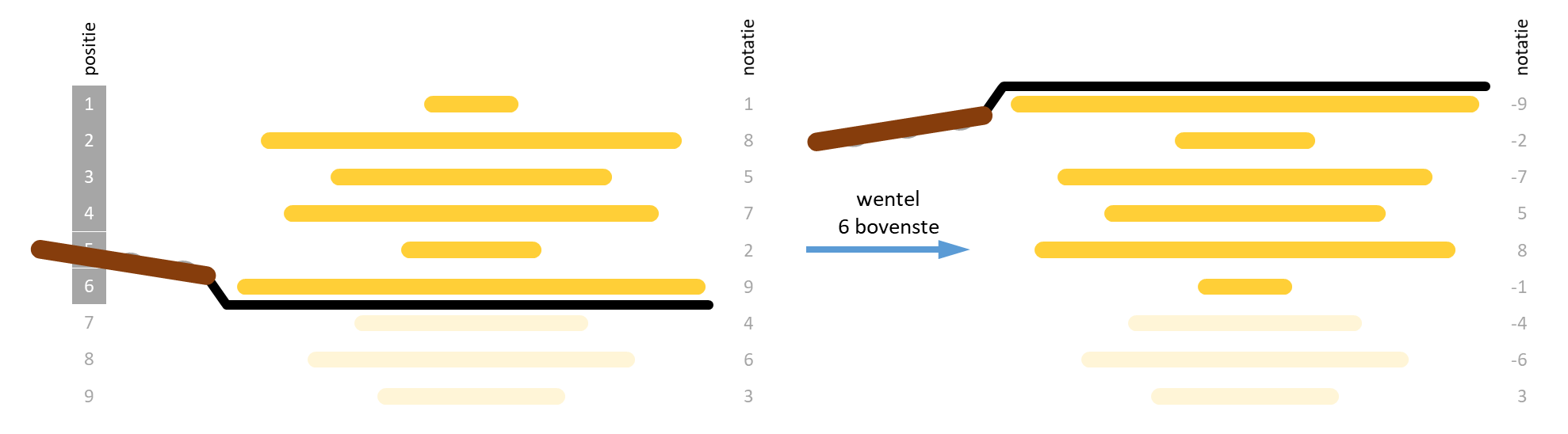
De uitdaging wordt nog groter als de chef-kok weer eens te diep in het glas gekeken heeft, waardoor hij de onderkant van alle pannenkoeken heeft laten aanbranden. De maitre d'hotel verwacht dan immers niet alleen dat zijn kelners de pannenkoeken van klein naar groot sorteren, maar dat ze er ook voor zorgen dat de aangebrande kant van de pannenkoeken van onder ligt.

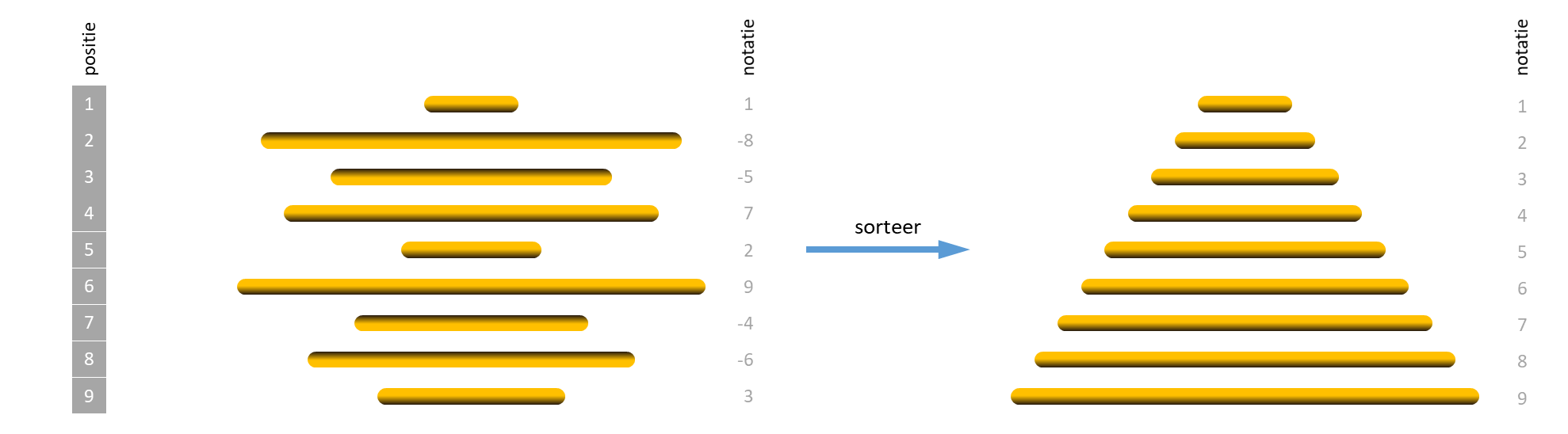
Bij het wentelen van een aantal aangebrande pannenkoeken aan de bovenkant van de stapel, verandert in dat geval niet alleen de volgorde van de pannenkoeken, maar keren ook alle pannenkoeken om. Daardoor zal een pannenkoek die met de aangebrande kant naar onder lag na het wentelen met de aangebrande kant naar boven liggen, en omgekeerd.

Er bestaat een eenvoudig algoritme om een stapel van $n$ pannenkoeken te sorteren. We leggen het uit door de posities van de pannenkoeken van boven naar onder te nummeren vanaf 1. Elke sorteerstap van het algoritme zorgt ervoor dat de grootste van de $m$ ($1\le m\le n$) bovenste pannenkoeken op positie $m$ komt te liggen, en ook met de aangebrande kant naar onder als het een stapel aangebrande pannenkoeken is.

1. zoek de positie $i$ ($1\le i\le m$) van de grootste pannenkoek in de bovenste $m$ pannenkoeken

2. wentel de bovenste $i$ pannenkoeken, waardoor de grootste pannenkoek bovenaan komt te liggen

3. enkel voor aangebrande pannenkoeken: wentel de bovenste pannenkoek als die met de aangebrande kant naar onder ligt, zodat die met de aangebrande kant naar boven komt te liggen

4. wentel de bovenste $m$ pannenkoeken waardoor de grootste pannenkoek op positie $m$ komt te liggen (en ook met de aangebrande kant naar onder als het een stapel aangebrande pannenkoeken is)

Om de volledige stapel pannenkoeken te sorteren, volstaat het dan om deze sorteerstap achtereenvolgens uit te voeren voor de bovenste $n$ pannenkoeken ($m=n$), de bovenste $n-1$ pannenkoeken ($m=n-1$), …, de bovenste $2$ pannenkoeken ($m=2$) en de bovenste pannenkoek ($m=1$).

Opgave

Een pannenkoek wordt voorgesteld door een getal $p\in {\mathbb{Z}}_0$ (int). Voor niet-aangebrande pannenkoeken geldt dat $p\in {\mathbb{N}}_0$, waarbij de waarde $p$ de grootte van de pannenkoek aangeeft. Voor aangebrande pannenkoeken geeft de absolute waarde $|p|$ de grootte van de pannenkoek aan en geeft het teken van $p$ aan waar de aangebrande kant ligt: onderaan als $p>0$ en bovenaan als $p<0$.

Een stapel van $n$ pannenkoeken wordt voorgesteld door een tuple (tuple) met de voorstellingen van de $n$ pannenkoeken in de stapel, opgelijst van boven naar onder. In een stapel zijn er nooit twee pannenkoeken met dezelfde grootte. Met andere woorden, de voorstelling van elke pannenkoek in de stapel heeft een unieke absolute waarde. In een stapel zijn ofwel alle pannenkoeken aan één kant aangebrand, ofwel zijn er geen aangebrande pannenkoeken.

Je opdracht bestaat erin om een gegeven stapel van $n\in {\mathbb{N}}_0$ pannenkoeken te sorteren aan de hand van het eenvoudig algoritme uit de inleiding. Hiervoor moet je de volgende functies schrijven, waaraan als eerste argument telkens een stapel met $n$ pannenkoeken moet doorgegeven worden. Behalve de functie zoek_grootste, hebben alle andere functies een optionele parameter aangebrand waaraan een Booleaanse waarde kan doorgegeven worden (standaardwaarde: False). Deze parameter geeft aan of de gegeven stapel pannenkoeken aangebrand is (True) of niet (False).

• Een functie wentel die de stapel pannenkoeken teruggeeft die men bekomt door alle pannenkoeken van de gegeven stapel te wentelen.

• Een functie wentel_bovenste waaraan een tweede verplicht argument $m$ ($1\le m\le n$, int) moet doorgegeven worden. De functie moet de stapel pannenkoeken teruggeven die men bekomt door de bovenste $m$ pannenkoeken van de gegeven stapel te wentelen.

• Een functie zoek_grootste waaraan een tweede verplicht argument $m$ ($1\le m\le n$, int) moet doorgegeven worden. De functie moet de positie teruggeven van de grootste pannenkoek uit de bovenste $m$ pannenkoeken van de gegeven stapel.

• Een functie sorteerstap waaraan een tweede verplicht argument $m$ ($1\le m\le n$, int) moet doorgegeven worden. De functie moet de stapel pannenkoeken teruggeven die men bekomt door de sorteerstap uit te voeren voor de bovenste $m$ pannenkoeken van de gegeven stapel.

• Een functie sorteerstappen die een lijst (list) met stapels pannenkoeken moet teruggeven. Het eerste element van de lijst is de gegeven stapel pannenkoeken. De functie moet de gegeven stapel pannenkoeken sorteren door de sorteerstap achtereenvolgens uit te voeren voor de bovenste $n$ pannenkoeken, de bovenste $n-1$ pannenkoeken, …, de bovenste $2$ pannenkoeken en de bovenste pannenkoek ($m=1$). Voor elke sorteerstap die wijzigingen aanbrengt aan de stapel pannenkoeken, moet de stapel pannenkoeken na het uitvoeren van de sorteerstap achteraan de lijst toegevoegd worden.

Voorbeeld

                
            >>> wentel((9, 2, 7, 5, 8, 1, 4, 6, 3))
(3, 6, 4, 1, 8, 5, 7, 2, 9)
>>> wentel((-9, -2, -7, 5, 8, -1, -4, -6, 3), aangebrand=True)
(-3, 6, 4, 1, -8, -5, 7, 2, 9)

>>> wentel_bovenste((1, 4, 6, 3, 5, 2, 7, 8, 9), 3)
(6, 4, 1, 3, 5, 2, 7, 8, 9)
>>> wentel_bovenste((6, 4, 1, 3, 5, 2, 7, 8, 9), 6)
(2, 5, 3, 1, 4, 6, 7, 8, 9)
>>> wentel_bovenste((-1, -4, -6, 3, -5, -2, 7, 8, 9), 3, aangebrand=True)
(6, 4, 1, 3, -5, -2, 7, 8, 9)
>>> wentel_bovenste((6, 4, 1, 3, -5, -2, 7, 8, 9), 1, aangebrand=True)
(-6, 4, 1, 3, -5, -2, 7, 8, 9)
>>> wentel_bovenste((-6, 4, 1, 3, -5, -2, 7, 8, 9), 6, aangebrand=True)
(2, 5, -3, -1, -4, 6, 7, 8, 9)

>>> zoek_grootste((1, 4, 6, 3, 5, 2, 7, 8, 9), 6)
3
>>> zoek_grootste((-1, -4, -6, 3, -5, -2, 7, 8, 9), 6)
3

>>> sorteerstap((1, 4, 6, 3, 5, 2, 7, 8, 9), 6)
(2, 5, 3, 1, 4, 6, 7, 8, 9)
>>> sorteerstap((-1, -4, -6, 3, -5, -2, 7, 8, 9), 6, aangebrand=True)
(2, 5, -3, -1, -4, 6, 7, 8, 9)

>>> sorteerstappen((1, 8, 5, 7, 2, 9, 4, 6, 3))
[(1, 8, 5, 7, 2, 9, 4, 6, 3), (3, 6, 4, 1, 8, 5, 7, 2, 9), (2, 7, 5, 3, 6, 4, 1, 8, 9), (1, 4, 6, 3, 5, 2, 7, 8, 9), (2, 5, 3, 1, 4, 6, 7, 8, 9), (4, 1, 3, 2, 5, 6, 7, 8, 9), (2, 3, 1, 4, 5, 6, 7, 8, 9), (1, 2, 3, 4, 5, 6, 7, 8, 9)]
>>> sorteerstappen((1, -8, -5, 7, 2, 9, -4, -6, 3), aangebrand=True)
[(1, -8, -5, 7, 2, 9, -4, -6, 3), (-3, 6, 4, 1, -8, -5, 7, 2, 9), (-2, -7, 5, -3, 6, 4, 1, 8, 9), (-1, -4, -6, 3, -5, -2, 7, 8, 9), (2, 5, -3, -1, -4, 6, 7, 8, 9), (4, 1, 3, 2, 5, 6, 7, 8, 9), (-2, -3, -1, 4, 5, 6, 7, 8, 9), (1, -2, 3, 4, 5, 6, 7, 8, 9), (1, 2, 3, 4, 5, 6, 7, 8, 9)]

Bronnen

• Cohen DS, Blum M (1995). On the problem of sorting burnt pancakes. Discrete Applied Mathematics 61(2), 105–120. ⁶

• Gates WH, Papadimitriou CH (1979). Bounds for sorting by prefix reversal. Discrete Mathematics 27(1), 47–57. ⁷

• Haynes KA, Broderick ML, Brown AD, Butner TL, Dickson JO, Harden WL, Heard LH, Jessen EL, Malloy KJ, Ogden BJ, Rosemond S (2008). Engineering bacteria to solve the burnt pancake problem. Journal of Biological Engineering 2(1), 8. ⁸