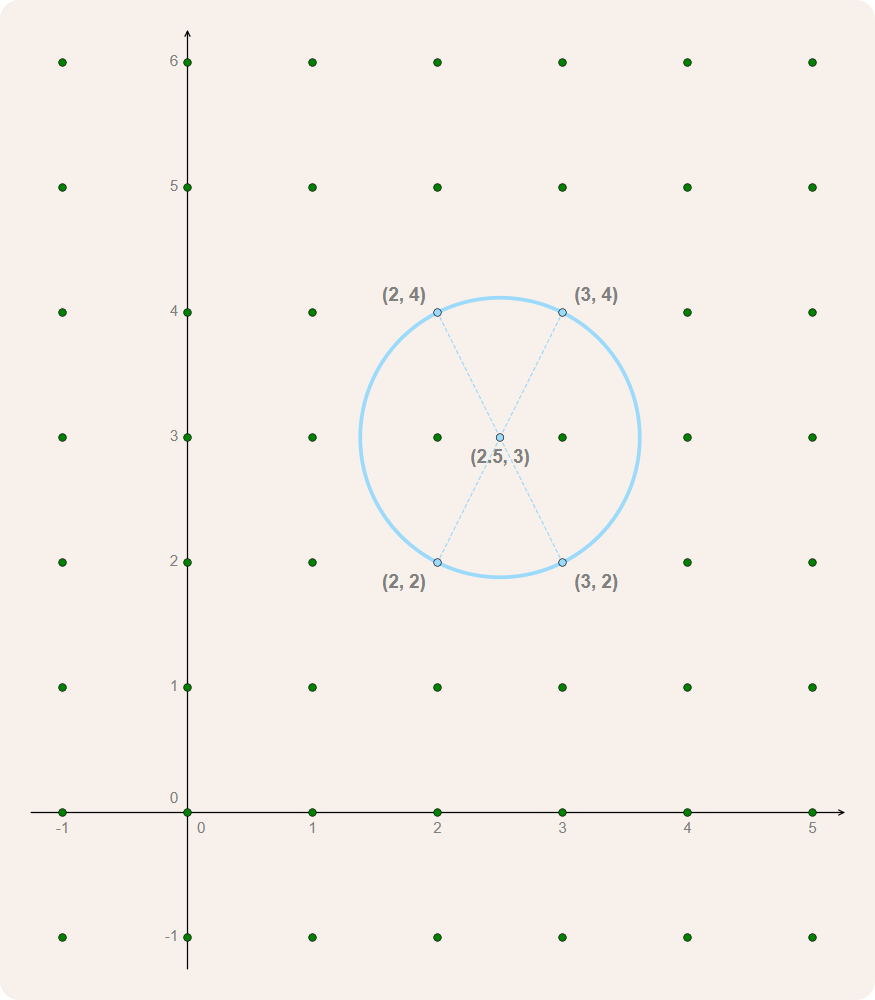
In 1958 bewees de Poolse wiskundige Andrzej Schinzel1 dat er voor elk getal $$n \in \mathbb{N}$$ een cirkel in het Euclidisch vlak bestaat die precies door $$n$$ roosterpunten gaat. De cirkel met middelpunt $$(2.5, 3)$$ en straal $$\frac{\sqrt{5}}{2}$$ gaat bijvoorbeeld door de vier roosterpunten $$(2, 4)$$, $$(3, 4)$$, $$(3, 2)$$ en $$(2, 2)$$.
Opgave
We stellen een punt in het Euclidisch vlak voor als een tuple $$(x, y)$$ met $$x, y \in \mathbb{R}$$ (float).
Een roosterpunt is een punt met gehele coördinaten. We stellen een roosterpunt voor als een tuple $$(x, y)$$ met $$x, y \in \mathbb{Z}$$ (int).
Een punt $$(x, y)$$ ligt op een cirkel met middelpunt $$(m_x, m_y)$$ en straal $$r$$ als en slechts als \[ (x - m_x)^2 + (y - m_y)^2 = r^2 \]
Reële getallen vergelijken
Als je werkt met floating point getallen, dan is het niet veilig om twee getallen $$a \in \mathbb{R}$$ (float) en $$b \in \mathbb{R}$$ (float) rechtstreeks met elkaar te vergelijken. In plaats daarvan stellen we dat $$a$$ en $$b$$ gelijk zijn als $$|a - b| < \epsilon$$. Hierbij staat $$|x|$$ voor de absolute waarde van $$x \in \mathbb{R}$$ en is $$\epsilon \in \mathbb{R}$$ een zeer kleine waarde die de tolerantie genoemd wordt. In deze opgave gebruiken we $$\epsilon = 10^{-6}$$ als tolerantie.
Het begrenzingsvak van de cirkel is de rechthoek met linkeronderhoek in het punt $$(\left \lfloor{m_x - r}\right \rfloor, \left \lfloor{m_y - r}\right \rfloor)$$ en rechterbovenhoek in het punt $$(\left \lceil{m_x + r}\right \rceil, \left \lceil{m_y + r}\right \rceil)$$. Hierbij staat $$\left \lfloor{x}\right \rfloor$$ voor het grootste geheel getal dat kleiner of gelijk is aan $$x \in \mathbb{R}$$ en $$\left \lceil{x}\right \rceil$$ voor het kleinste geheel getal dat groter of gelijk is aan $$x \in \mathbb{R}$$. De cirkel met middelpunt $$(2.5, 3)$$ en straal $$\frac{\sqrt{5}}{2}$$ heeft bijvoorbeeld een begrenzingsvak met linkeronderhoek in het punt $$(1, 1)$$ en rechterbovenhoek in het punt $$(4, 5)$$.
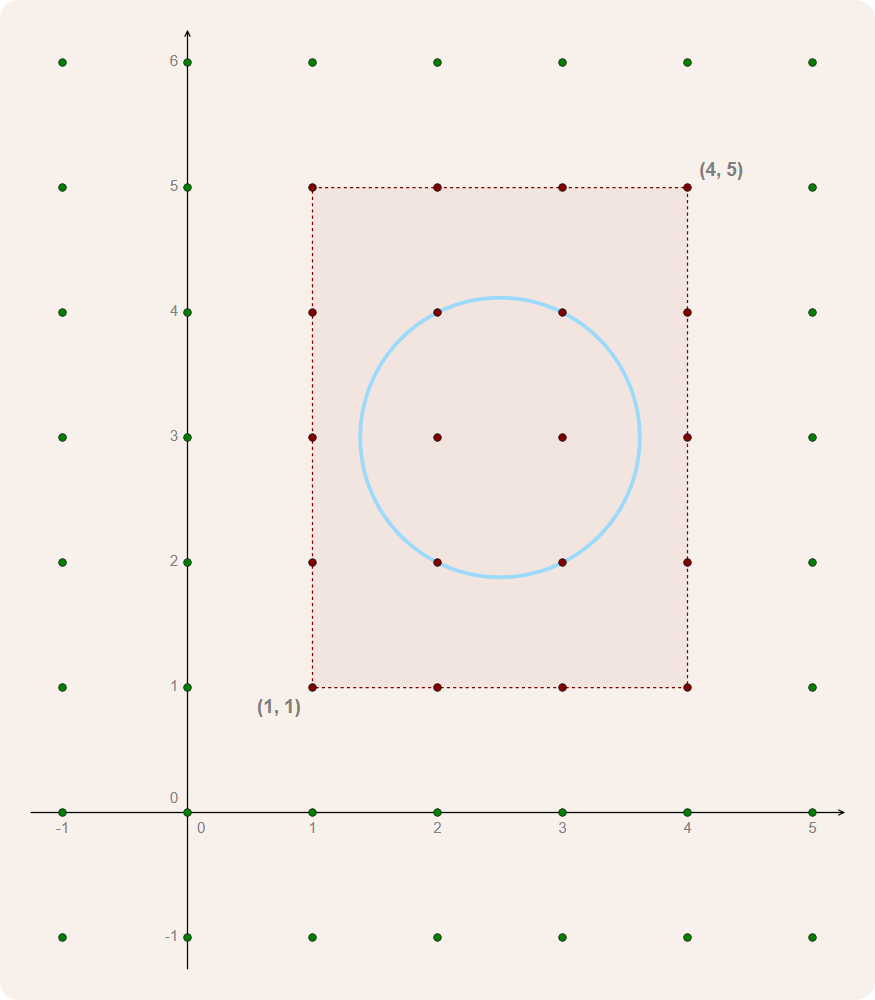
Om te bepalen door welke roosterpunten een cirkel met middelpunt $$(m_x, m_y)$$ en straal $$r$$ gaat, kunnen we alle roosterpunten binnen het begrenzingsvak van de cirkel overlopen om te controleren of ze op de cirkel liggen.
Gevraagd wordt:
-
Schrijf een functie punt_op_cirkel waaraan drie argumenten moeten doorgegeven worden: i) een punt $$p$$ (tuple), ii) het middelpunt $$m$$ (tuple) van een cirkel en iii) de straal $$r$$ (float) van de cirkel. De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of punt $$p$$ op de cirkel met middelpunt $$m$$ en straal $$r$$ ligt.
-
Schrijf een functie begrenzingsvak waaraan het middelpunt $$m$$ (tuple) en de straal $$r$$ (float) van een cirkel moeten doorgegeven worden. De functie moet een tuple teruggeven met de linkeronderhoek (tuple) en de rechterbovenhoek (tuple) van het begrenzingsvak van de cirkel met middelpunt $$m$$ en straal $$r$$.
-
Schrijf een functie roosterpunten waaraan het middelpunt $$m$$ (tuple) en de straal $$r$$ (float) van een cirkel moeten doorgegeven worden. De functie moet een verzameling (set) teruggeven met alle roosterpunten (tuple) die op de cirkel liggen met middelpunt $$m$$ en straal $$r$$.
Voorbeeld
>>> punt_op_cirkel((2, 4), (2.5, 3), 5 ** 0.5 / 2)
True
>>> punt_op_cirkel((1, 3), (2.5, 3), 5 ** 0.5 / 2)
False
>>> begrenzingsvak((2.5, 3), 5 ** 0.5 / 2)
((1, 1), (4, 5))
>>> begrenzingsvak((4 / 3, 2), 5 ** 2 / 3)
((-8, -7), (10, 11))
>>> roosterpunten((2.5, 3), 5 ** 0.5 / 2)
{(2, 4), (3, 2), (3, 4), (2, 2)}
>>> roosterpunten((4 / 3, 2), 5 ** 2 / 3)
{(8, 7), (8, -3), (-1, 10), (-1, -6), (-7, 2)}