Een voorbeeld van een recursieve definitie is de definitie van de faculteit, die ik al heb geïntroduceerd in twee eerdere hoofdstukken. In die hoofdstukken gaf ik de volgende definitie van de faculteit: de faculteit van een positief geheel getal is dat getal, vermenigvuldigd met alle positieve gehele getallen die kleiner zijn (exclusief nul).

Wiskundigen prefereren een recursieve definitie: De faculteit \(n!\) van een positief getal \(n\) wordt als volgt berekend: \(1! = 1\), en \(n! = n * (n-1)!\) voor \(n > 1\).

Deze definitie is recursief omdat het refereert aan de faculteit van \(n-1\) om de faculteit van \(n\) te definiëren. Dit leidt niet tot eindeloze recursie, omdat op enig moment \(n\) gelijk zal zijn aan \(1\), en de faculteit van \(1\) is apart gedefinieerd.

Je kunt de faculteit als een recursieve functie als volgt implementeren:

def faculteit( n ):
    if n <= 1:
        return 1
    return n * faculteit( n-1 )

print( faculteit( 5 ) )

Zie hoe deze functie exact de recursieve definitie van de faculteit volgt: als n gelijk is aan 1, retourneert de functie 1, en anders retourneert het n keer de faculteit van n-1. (Merk op dat ik n <= 1 schreef in plaats van n == 1 om te voorkomen dat er problemen ontstaan als de gebruiker de functie aanroept met, bijvoorbeeld, een negatieve n.)

Voor het geval je het problematisch vindt om te begrijpen wat deze functie doet, beschrijf ik hieronder de aanroepen die de functie doet als hij wordt aangeroepen met 5 als argument. Ik laat aanroepen inspringen als een “hoger-niveau aanroep” nog steeds actief is als de aanroep wordt gemaakt. Een “return” die één inspringing dieper gaat dan een “aanroep,” wordt gegeven in die aanroep, en retourneert de gegeven waarde.

aanroep faculteit( 5 )
    aanroep faculteit( 4 )
        aanroep faculteit( 3 )
            aanroep faculteit( 2 )
                aanroep faculteit( 1 )
                    return 1
                return 2 * 1
            return 3 * 2
        return 4 * 6
    return 5 * 24
print( 120 )

Wanneer gebruik je recursie

Als je doorhebt hoe de recursieve implementatie van de faculteit werkt, ziet het er wellicht aantrekkelijk uit. Het is eenvoudig, elegant, en is eigenlijk best wel “cool.” Echter, de iteratieve implementatie van de faculteit is zeer te prefereren boven de recursieve.

De reden blijkt uit de beschrijving van de aanroepen hierboven. Je ziet dat voordat de aanroep faculteit( 1 ) wordt gemaakt, er al vier aanroepen van faculteit() in het geheugen van de computer staan. Als je de faculteit van 100 zou willen berekenen, komen er niet minder dan 100 aanroepen van faculteit in het geheugen te staan alvorens er waardes geretourneerd gaan worden. Dit is geen goed idee, en Python zou gebrek aan (stack) geheugen kunnen krijgen, of heel, heel erg traag worden.

Daartegenover staat dat een iteratieve implementatie van de faculteit slechts twee variabelen in het geheugen hoeft te houden. Dat is snel en geeft geen gevaar dat de computer vastloopt. Je moet alleen recursieve implementaties bouwen als:

• recursie de meest natuurlijke manier is om de oplossing te implementeren; en

• het recursieve proces gegarandeerd niet te diep gaat.

Iedere recursieve functie kan ook als een iteratief proces gebouwd worden. Zo nu en dan kom je echter een probleem tegen waarvoor de recursieve oplossing veel eleganter, leesbaarder, en onderhoudbaarder is dan de iteratieve variant. In dat geval moet je overwegen een recursieve oplossing te implementeren.

Doolhof doorzoeken

Op dit punt in het boek is het lastig een goede demonstratie van recursie te geven, aangezien het specifieke data structuren¹¹ nodig heeft om de kracht te tonen. Om toch iets niet-triviaals te tonen, heb ik een module genaamd pcmaze gecreëerd. Je vindt deze module in appendix 32, en je moet hem ofwel zelf maken, ofwel downloaden van dezelfde site waar je pcinput.py hebt gevonden, om de code van deze paragraaf te kunnen uitvoeren.

pcmaze implementeert een eenvoudig doolhof, dat een aantal genummerde cellen met elkaar verbindt. De ingang van het doolhof kun je vinden door aanroep van de functie entrance().²² De uitgang van het doolhof wordt gegeven door de functie exit() (niet te verwarren met de exit() functie uit de sys module). De module heeft ook een functie connected() die twee numerieke argumenten krijgt: deze retourneert True als er een directe verbinding bestaat tussen de cellen met die nummers, en anders False. De ingang is gegarandeerd de laagst-genummerde cel, en de uitgang is gegarandeerd de hoogst-genummerde cel.

Het doel is code te schrijven die een pad uitzet van de ingang naar de uitgang (als een dergelijk pad bestaat). Het doolhof is gevisualiseerd in afbeelding 10.1³. De ingang is 1, de uitgang is 16.

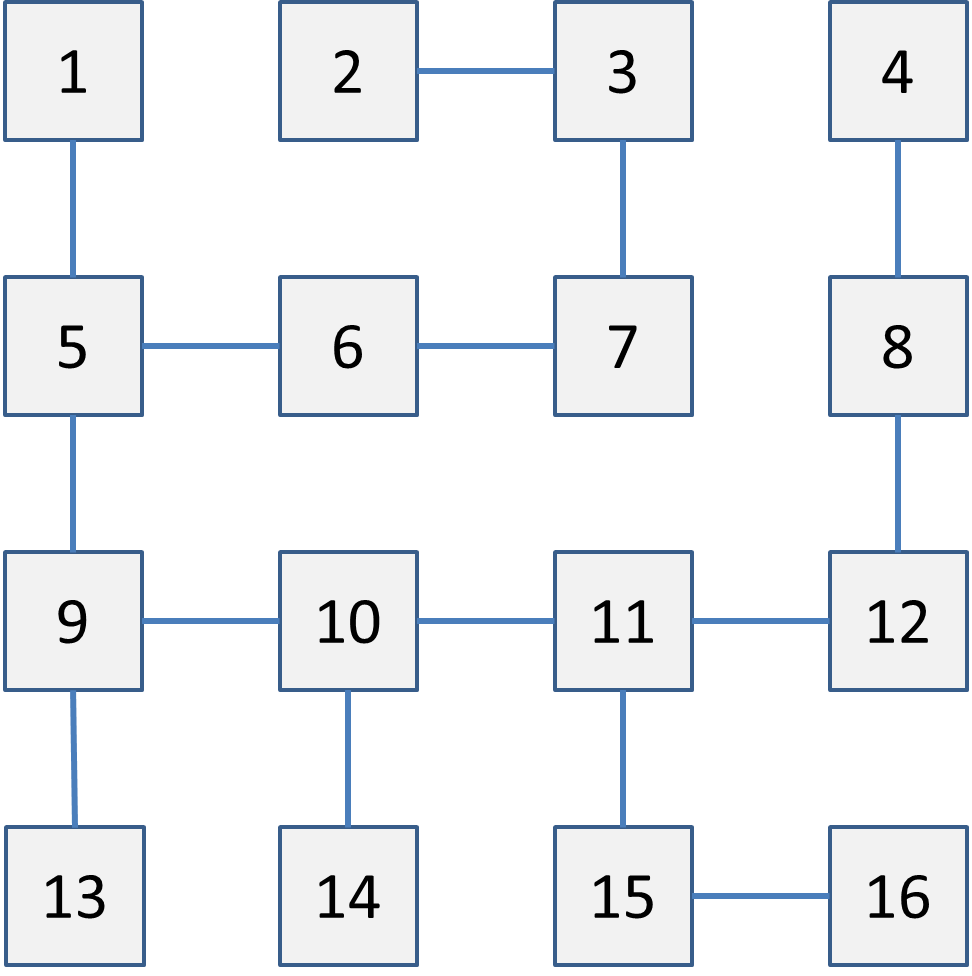
Hoe vind je nu je weg door zo’n doolhof (zonder dat je de layout kent)? Recursief kan dat als volgt: Je definieert een functie leidt_naar_uitgang() die een pad naar de uitgang retourneert als de cel die als parameter wordt meegegeven op het pad ligt dat naar de uitgang leidt. Als die functie een pad retourneert, dan weet je dat de huidige cel op dat pad ligt. Als je hem dus aanroept met cel 1, krijg je een pad dat leidt van de ingang naar de uitgang (als dat pad er is).

Maar hoe weet de functie of een cel ligt op het pad dat leidt naar de uitgang? Als de huidige cel de uitgang zelf is, dan weet je dat, jazeker, deze cel op dat pad ligt. Zo niet, dan ligt de cel op het pad dat leidt naar de uitgang als het een verbinding heeft met een cel die ligt op het pad dat leidt naar de uitgang. Dit is een recursieve definitie.

Je moet voorzichtig zijn met zo’n recursieve definitie dat je niet vastloopt op een circulair pad in het doolhof. Dat betekent dat als de functie “beweegt” van cel A naar cel B, de functie niet meer terug mag komen bij A. Als dat gegarandeerd is, moet de functie werken. De eenvoudige implementatie die ik hier ga geven zou niet werken als er circulaire paden in het doolhof zouden zijn, maar die zijn er gelukkig niet. Het probleem is niet onoplosbaar als ze er wel zijn, maar om dat netjes op te lossen heb je een data structuur nodig die pas in een toekomstig hoofdstuk aan bod komt.

In pseudo-code ziet de recursieve functie leidt_naar_uitgang() er ongeveer als volgt uit:

functie leidt_naar_uitgang( huidigecel ):
    if (huidigecel is de uitgang):
        return (pad dat alleen de uitgang bevat)
    for (iedere verbondencel die nog niet onderzocht is):
        pad = leidt_naar_uitgang( verbondencel )
        if (pad is niet leeg):
            voeg huidigecel toe aan pad
            return pad
    return (leeg pad)

Ik geef nu een implementatie van deze recursieve oplossing. In de implementatie meteen hieronder geef ik niet het pad terug, maar ik retourneer gewoon True of False om aan te geven of het pad gevonden is, en ik print het pad in de functie zelf (ik zal later in dit hoofdstuk een complete implementatie van de pseudo-code geven).

from pcmaze import entrance, exit, connected

def leidt_naar_uitgang( komtvan, cel ):
    if cel == exit():
        return True
    for i in range( entrance(), exit()+1 ):
        if i == komtvan:
            continue
        if not connected( cel, i ):
            continue
        if leidt_naar_uitgang( cel, i ):
            print( cel, "->", i )
            return True
    return False

if leidt_naar_uitgang( 0, entrance() ):
    print( "Pad gevonden!" )
else:
    print( "Pad niet gevonden" )

Ik bespreek deze recursieve functie nu in detail.

De functie krijgt twee parameters. De eerste is de cel waar het pad vandaan komt. De tweede is de cel die gecontroleerd wordt om te zien of hij naar de uitgang leidt. De eerste parameter is alleen nodig omdat je niet mag terugkeren op het pad.

De functie controleert eerst of de uitgang bereikt is. Zo ja, dan retourneert de functie True.

Als de uitgang niet bereikt is, controleert de functie alle cellen van het doolhof om te zien of ze verbonden zijn met de huidige cel.

De cel waarvandaan de aanroep gekomen is wordt uitgesloten. Ook worden alle cellen uitgesloten waarmee geen verbinding is. Maar alle overige cellen worden gecontroleerd. De cel zelf hoeft niet uitgesloten te worden, aangezien in de definitie van het doolhof een cel nooit verbonden is met zichzelf.

Als een cel blijkt naar de uitgang te leiden (doordat de recursieve aanroep True geeft), dan drukt de functie af dat de beweging “huidige cel naar gecontroleerde cel” deel is van het pad dat naar de uitgang leidt. Vervolgens retourneert de functie True.

Anders, nadat alle verbonden cellen zijn gecontroleerd en nog steeds geen pad is gevonden, retourneert de functie False.

Deze aanpak zal het volledige pad van ingang naar uitgang afdrukken, in omgekeerde volgorde.

Om duidelijk te maken wat er precies gebeurt in de functie, heb ik hem wat uitgebreid. De implementatie hieronder drukt iedere verbinding die gecontroleerd wordt af. Ik heb ook een parameter diepte toegevoegd, die bijhoudt hoe diep de recursie gaat. Ik vertaal die diepte in inspringingen.

from pcmaze import entrance, exit, connected

def leidt_naar_uitgang( komtvan, cel, diepte ):
    inspringing = diepte * 4 * " "
    if cel == exit():
        return True
    for i in range( entrance(), exit()+1 ):
        if i == komtvan:
            continue
        if not connected( cel, i ):
            continue
        print( inspringing + "Controleer", cel, "->", i )
        if leidt_naar_uitgang( cel, i, diepte + 1 ):
            print( inspringing + "Pad gevonden:", cel, "->", i )
            return True
    return False

if leidt_naar_uitgang( 0, entrance(), 0 ):
    print( "Pad gevonden!" )
else:
    print( "Pad niet gevonden" )

Retourwaardes van recursieve functies

Net als reguliere functies, kunnen recursieve functie informatie communiceren aan de rest van het programma middels retourwaardes.

Een van de minder-fraaie zaken van de doolhof-oplossende functie hierboven is dat het pad geprint wordt in plaats van geretourneerd – wat er ook toe leidt dat het pad in omgekeerde volgorde wordt afgedrukt. Het zou beter zijn als de functie aanroepen hun deel van het pad aan een hoger liggende aanroep zouden retourneren, zodat uiteindelijk het pad als geheel zou worden geretourneerd naar de eerste aanroep. Dit is wat de pseudo-code beoogde. Een goede manier om een pad te retourneren is in de vorm van een list, maar dat is het onderwerp van hoofdstuk 13. In plaats daarvan doe ik het als een string.

Het werkt als volgt: een aanroep die de uitgang vindt, retourneert het nummer van de uitgang als string. Een aanroep die een deel van het pad geretourneerd krijgt, retourneert dat pad zelf ook weer, maar voegt de huidige cel toe aan het pad. Een aanroep die een lege string terugkrijgt, retourneert zelf ook een lege string.

Dit betekent dat in de code hierboven, iedere return True vervangen moet worden door een commando dat een string retourneert dat een (deel van het) pad retourneert, en iedere return False vervangen moet worden door het retourneren van een lege string. De code wordt dan:

from pcmaze import entrance, exit, connected

def leidt_naar_uitgang( komtvan, cel ):
    if cel == exit():
        return "{}".format( exit() )
    for i in range( entrance(), exit()+1 ):
        if i == komtvan:
            continue
        if not connected( cel, i ):
            continue
        check = leidt_naar_uitgang( cel, i )
        if check != "":
            return "{} -> {}".format( cel, check )
    return ""

check = leidt_naar_uitgang( 0, entrance() )
if check != "":
    print( "Pad gevonden!", check )
else:
    print( "Pad niet gevonden" )

Als je recursie wilt begrijpen, moet je deze code goed bestuderen. De code is een typische weergave van het gebruik van retourwaardes in recursieve functies. Studenten wiens begrip van recursie wankel is en die een opdracht krijgen waar informatie van een dieper niveau van recursie naar een hoger niveau van recursie gecommuniceerd moet worden, grijpen vaak naar een globale variabele om dit te doen. Je ziet dat dat niet nodig is.

Feitelijk is er geen echt verschil tussen een recursieve functie aanroep en een reguliere functie aanroep, behalve dat je bij recursieve aanroepen ervoor moet zorgen dat ze wel op een bepaald moment eindigen. Recursie ziet er alleen vreemd uit de eerste keer dat je het tegenkomt.